В шероховатых трубах. График И.И. Никурадзе

Потери напора при турбулентном течении

Для гидравлически гладких труб коэффициент потерь на трение вполне определяется числом Re. Для шероховатых труб 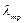, зависит еще и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т.е. так называемая относительная шероховатость 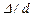. Одна и та же абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости.

При так называемой равномерно распределенной зернистой шероховатости. В этом случае коэффициент зависит как от Re, так и от отношения 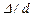(или ):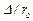

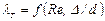. (12.5)

Характер влияния этих двух параметров на сопротивление труб отчетливо виден из графика, который является результатом опытов И.И. Никурадзе по испытанию на сопротивление ряда труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределенная зернистая шероховатость. Испытания были проведены при широком диапазоне относительных шероховатостей , а также чисел Re . Результаты этих испытаний представлены на рис. 12.2, где построены кривые зависимости 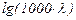от для ряда значений .

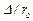Рис. 12.2. Зависимость 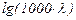от для труб

с искусственной шероховатостью

Наклонные прямые А и В соответствуют законам сопротивления гладких труб. После умножения на 1000 и логарифмирования получим уравнения прямых

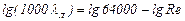; (12.6)

. (12.7)

Штриховыми линиями показаны кривые для труб с различной относительной шероховатостью .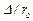

Из рассмотрения графика можно сделать следующие основные выводы.

1. При ламинарном течении шероховатость на сопротивление не влияет; штриховые кривые, соответствующие различным шероховатостям, практически совпадают с прямой А.

2. Критическое число Re от шероховатости практически не зависит; штриховые кривые отклоняются от прямой А приблизительно при одном и том же .

3. В области турбулентного течения, но при небольших Re и 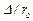шероховатость на сопротивление не влияет; штриховые линии на некоторых участках совпадают с прямой В. Однако при увеличении Re это влияние начинает сказываться, и кривые для шероховатых труб начинают отклоняться от прямой, соответствующей закону сопротивления гладких труб.

4. При больших Re и больших относительных шероховатостях коэффициент перестает зависеть от Re и становится постоянным для данной относительной шероховатости. Это соответствует тем участкам штриховых кривых, где они после некоторого подъема располагаются параллельно оси абсцисс.

Таким образом, для каждой из кривых, соответствующих шероховатым трубам при турбулентном течении, можно отметить следующие три области значений Re и 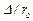, отличающиеся друг от друга характером изменения коэффициента .

Первая область - область малых Re и 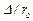, где коэффициент от шероховатости не зависит, а определяется лишь числом Re; это область гидравлически гладких труб. Она не имеет места для максимальных значений шероховатости в опытах И. И. Никурадзе.

Во второй области коэффициент зависит одновременно от двух параметров - числа Re и относительной шероховатости.

Третья область - область больших Re и 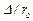, где коэффициент не зависит от Re, а определяется лишь относительной шероховатостью. Эту область называют областью автомодельности или режимом квадратичного сопротивления, так как независимость коэффициента от Re означает, что потеря напора пропорциональна скорости во второй степени.

Это объясняется тем, что при малых числах Re толщина вязкого подслоя турбулентного течения оказывается больше высоты бугорков шероховатости, последние находятся внутри вязкого подслоя, обтекаются плавно (безотрывно) и на сопротивление не влияют.

По мере увеличения Re толщина уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на сопротивление. При больших Re толщина ламинарного слоя становится весьма малой, а бугорки шероховатости обтекаются турбулентным потоком с вихреобразованиями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, характерный для данной области.

Опыты Никурадзе проводились на трубах, снабженных искусственной, равномерно распределенной зернистой шероховатостью. Для натуральных шероховатых труб закон изменения от Re получается несколько иным, без подъема кривых после отклонения их от закона для гладких труб.

Это объясняется тем, что в натурной трубе бугорки шероховатости имеют различную высоту и при увеличении числа Re начинают выступать за пределы ламинарного слоя не одновременно, а при разных Re. Ввиду этого переход от линии, соответствующей сопротивлению гладких труб, к горизонтальным прямым, соответствующим квадратичному закону, происходит для натурных труб более плавно, без провала кривых.

Для практических расчетов по определению сопротивления реальных шероховатых труб можно рекомендовать универсальную формулу А. Д. Альтшуля

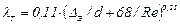, (12.8)

где - эквивалентная абсолютная шероховатость;

d - диаметр трубы.

При 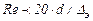формула (12.8) переходит в приведенную выше формулу (12.4) Блазиуса для гладких труб.

При для вычисления коэффициента гидравлического трения (Дарси) можно также рекомендовать формулу Никурадзе-Лиса

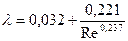. (12.9)

При для вполне шероховатых труб, т.е. для режима квадратичного сопротивления (автомодельности) расчет величины коэффициента гидравлического трения производят по формуле Шифринсона

, (12.10)

либо по формуле Никурадзе-Блантера

. (12.11)

Таким образом, путем сравнения численного значения отношения с числом Re можно установить границы указанных выше областей (режимов) турбулентного течения в шероховатых трубах.

Дата добавления: 2014-10-31