Стенке при постоянном напоре

Истечение жидкости через отверстие в тонкой

ЛЕКЦИЯ №14

Истечение жидкости из резервуаров, баков, котлов через отверстия и насадки (короткие трубки разной формы) характерно тем, что в процессе истечения запас потенциальной энергии, которым обладает жидкость в резервуаре, превращается с большими или меньшими потерями в кинетическую энергию свободной струи или капель. Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.

Рассмотрим большой резервуар с жидкостью под давлением р₀, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н₀ от свободной поверхности (рис. 14.1). Через это отверстие жидкость вытекает в воздушное (газовое) пространство с давлением р₁.

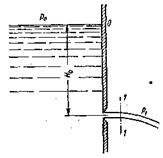
Рис. 14.1. Истечение из резервуара через малое отверстие

Пусть отверстие имеет форму, показанную на рис. 14.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис. 14.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны.

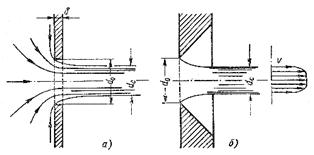
Рис. 14.2. Истечение через круглое отверстие

Условия истечения жидкости в этих двух случаях будут совершенно одинаковыми: частицы жидкости приближаются к отверстию из всего прилежащего объема, двигаясь ускоренно по различным плавным траекториям (рис. 14.2, а). Струя отрывается от стенки у кромки отверстия и затем несколько сжимается. Цилиндрическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения жидкости в резервуаре, в том числе от радиального движения по стенке, к осевому движению в струе.

Так как размер отверстия предполагается малым по сравнение с напором Н₀ и размерами резервуара, и следовательно, его боковые стенки и свободная поверхность жидкости не влияют на приток жидкости к отверстию, то наблюдается совершенное сжатие струи, т.е. наибольшее сжатие в отличие от несовершенного сжатия. Степень сжатия оценивается коэффициентом сжатия ε, равным отношению площади сжатого поперечного сечения струи к площади отверстия

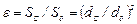. (14.1)

Запишем уравнение Д. Бернулли для движения жидкости от свободной поверхности в резервуаре (сечение 0-0 на рис. 14.1), где давление р₀, а скорость можно считать равной нулю, до одного из сечений струи (сечение 1-1) в той ее части, где она уже приняла цилиндрическую форму, а давление в ней, следовательно, сделалось равным давлению р₁ окружающей среды. В результате будем иметь:

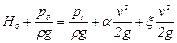, (14.2)

где 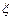- коэффициент сопротивления отверстия.

Вводя расчетный напор 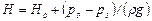, получаем

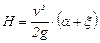, (14.3)

отсюда скорость истечения

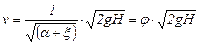, (14.4)

где 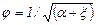- коэффициент скорости.

В случае идеальной жидкости ξ = 0, α = 1, следовательно, φ = 1 и скорость истечения идеальной жидкости

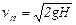. (14.5)

Из рассмотрения формулы (14.4) можно заключить, что коэффициент скорости φ есть отношение действительной скорости истечения к скорости истечения идеальной жидкости

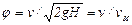. (14.6)

Действительная скорость истечения v всегда несколько меньше идеальной из-за сопротивления, следовательно, коэффициент скорости всегда меньше единицы.

Распределение скоростей по сечению струи является равномерным лишь в средней части сечения (в ядре струи), наружный же слой жидкости несколько заторможен из-за трения о стенку (рис. 14.2, б). Как показывают опыты, скорость в ядре струи практически равна идеальной, поэтому введенный коэффициент скорости φ следует рассматривать как коэффициент средней скорости. Если истечение происходит в атмосферу, то давление по всему сечению цилиндрической струи равно атмосферному.

Подсчитаем расход жидкости как произведение действительной скорости истечения на фактическую площадь сечения струи, а затем, используя соотношения (14.1) и (14.4), получим

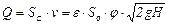. (14.7)

Произведение коэффициентов ε и φ принято обозначать буквой μ и называть коэффициентом расхода, т.е.

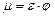. (14.8)

Тогда формулу (14.7) можно окончательно записать так

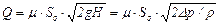, (14.9)

где 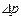- расчетная разность давлений, под действием которой происходит истечение.

При помощи выражения (14.9) решается основная задача - определяется расход. Трудность использования этого выражения заключается в достаточно точной оценке коэффициента расхода μ. Из уравнения (14.9) следует, что

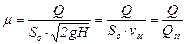. (14.10)

Это значит, что коэффициент расхода есть отношение действительного расхода к тому расходу Q'_и, который имел бы место при отсутствии сжатия струи и сопротивления. Величина Q'_и не является расходом при истечении идеальной жидкости, так как сжатие струи будет иметь место и при отсутствии гидравлических потерь. Действительный расход всегда меньше теоретического, и, следовательно, коэффициент μ расхода всегда меньше единицы вследствие влияния двух факторов: сжатия струи и сопротивления. В одних случаях больше влияет первый фактор, в других - второй.

Введенные в рассмотрение коэффициенты сжатия ε, сопротивления ξ, скорости φ и расхода μ зависят в первую очередь от типа отверстия и насадка, а также, как и все безразмерные коэффициенты в гидравлике, от основного критерия гидродинамического подобия - числа Re.

На рис. 14.3 показаны зависимости коэффициентов ε, φ и μ для круглого отверстия от Re_и, подсчитанного по идеальной скорости истечения, т.е.

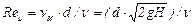. (14.11)

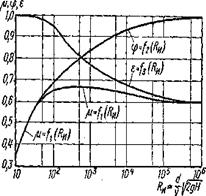
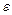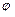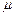Рис. 14.3. Зависимости , и от 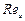для круглого

отверстия в тонкой стенке

Из графика видно, что с увеличением Re_и, т.е. с уменьшением влияния сил вязкости, коэффициент φ возрастает в связи с уменьшением коэффициента сопротивления ξ, а коэффициент ε уменьшается вследствие уменьшения торможения жидкости у кромки отверстия и увеличения радиусов кривизны поверхности струи на ее участке от кромки до начала цилиндрической части. Значения коэффициентов φ и ε при этом асимптотически приближаются к их значениям, соответствующим истечению идеальной жидкости, т.е. при Re_и→ ∞ со значения φ→ 1 и ε → 0,6. Это близко к теоретически найденному Кирхгофом значению ε при истечении идеальной жидкости через плоскую щель

ε _и = π / (2 + π). (14.12)

Коэффициент расхода μ, определяемый произведением ε на φ, с увеличением Re сначала увеличивается, что обусловлено крутым возрастанием φ, а затем, достигнув максимального значения (μ_max = 0,69 при Re_и= 350), уменьшается в связи со значительным падением ε и при больших Re_и, практически стабилизируется на значении, равном μ = 0,60...0,61.

В области весьма малых Re_и (Re_и<25) роль вязкости настолько велика, а торможение жидкости у кромки столь значительно, что сжатие струи отсутствует (ε = 1) и φ = μ. В этом случае можно пользоваться формулой, вытекающей из теоретического решения Веста:

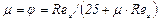, (14.13)

откуда

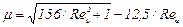. (14.14)

Для маловязких жидкостей (воды, бензина, керосина и др.), истечение которых обычно происходит при достаточно больших числах Re, коэффициенты истечения изменяются в небольших пределах. В расчетах обычно принимают следующие их осредненные значения: ε= 0,64; φ = 0,97; 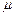= 0,62; 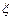= 0,065. При истечении маловязких жидкостей через круглое отверстие в тонкой стенке имеет место значительное сжатие струи и весьма небольшое сопротивление, поэтому коэффициент расхода μ получается значительно меньше единицы, главным образом, за счет влияния сжатия струи.

Дата добавления: 2014-10-31