При переменном напоре

Истечение через отверстия и насадки

ЛЕКЦИЯ №15

Рассмотрим опорожнение открытого в атмосферу сосуда произвольной формы через донное отверстие или насадок с коэффициентом μ (рис. 15.1). В этом случае истечение будет происходить при переменном, постепенно уменьшающемся напоре, т.е., строго говоря, течение является, неустановившимся.

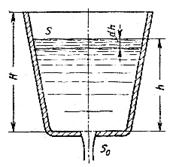
Рис. 15.1. Схема опорожнения резервуара

Если напор, а, следовательно, и скорость истечения изменяются медленно, то движение в каждый данный момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Д. Бернулли (квазистационарное течение). Обозначив переменную высоту уровня жидкости в сосуде, отсчитываемую от дна, через h, площадь сечения резервуара на этом уровне S, а площадь отверстия S₀ и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

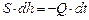или 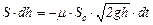, (15.1)

где dh - изменение уровня жидкости в сосуде за время dt.

Знак минус обусловлен тем, что положительному приращению dt соответствует отрицательное приращение dh.

Отсюда время полного опорожнения сосуда высотой Н найдем следующим путем (считая μ = const):

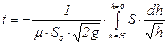. (15.2)

Интеграл можно подсчитать, если известен закон изменения площади S по высоте h. Для цилиндрического сосуда S = const, следовательно

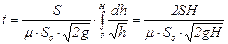. (15.3)

Числитель этой формулы равен удвоенному объему сосуда, а знаменатель представляет собой расход в начальный момент опорожнения, т.е. при напоре Н. Следовательно, время полного опорожнения сосуда в 2 раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

Дата добавления: 2014-10-31