Неустановившееся движение жидкости в трубах

Неустановившимся, или нестационарным, движением жидкости называется движение, переменное по времени. При этом движении как вектор скорости, так и давление в жидкости являются функциями не только координат точки, но и времени. Таким образом 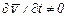и .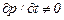

В потоке идеальной несжимаемой жидкости выделим элемент струйки длиной dl и площадью сечения dS (рис. 15.2). Применим к массе этого элемента второй закон Ньютона, причем уравнение запишем в проекции на направление касательной к осевой линии струйки. Будем иметь

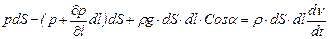
или

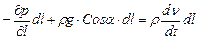. (15.4)

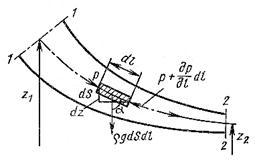
Рис. 15.2. Схема для вывода уравнения

неустановившегося течения

Частная производная от давления p использована потому, что давление, так же как и скорость 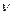, является функцией двух переменных - l и t, а уравнение движения записано для определенного момента времени. В правой же части уравнения записана полная производная от v по t, т.е. полное ускорение, которое равно сумме локального (местного) ускорения, обусловленного нестационарностью движения, и конвективного ускорения, определяемого геометрией потока, т.е.

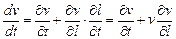. (15.5)

Учитывая, что 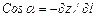, где z - вертикальная координата, перепишем уравнение движения в виде:

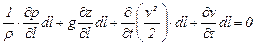. (15.6)

Интегрируя вдоль струйки от сечения 1-1 до сечения 2-2 в тот же фиксированный момент времени, получаем:

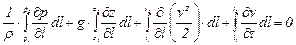
или

. (15.7)

После деления на g и перегруппировки членов уравнения будем иметь:

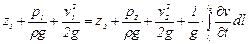. (15.18)

Полученное уравнение отличается от уравнения Д. Бернулли для струйки идеальной жидкости лишь четвертым членом в правой части, который называется инерционным напором:

. (15.19)

Из уравнения (15.19) ясен физический смысл инерционного напора 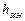: это есть разность полных напоров (полных энергий жидкости, отнесенных к единице веса жидкости) в сечениях 1-1 и 2-2 в данный фиксированный момент времени, обусловленная ускорением (или торможением) потока жидкости.

Для неустановившегося потока вязкой жидкости необходимо учесть еще неравномерность распределения скоростей и потери напора, следовательно, уравнение (15.18) будет иметь вид

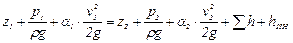. (15.20)

Для трубы постоянного диаметра локальное ускорение 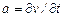также постоянно вдоль трубы, следовательно, инерционный напор

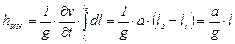. (15.21)

Все сказанное относится лишь к определенному моменту времени или к равноускоренному движению жидкости (а = const). При переменной величине а характер распределения напоров вдоль потока изменяется с течением времени.

Гидравлические потери при неустановившемся движении отличны от потерь при установившемся движении. Это связано с видоизменением профиля скоростей по сечению трубы. Так, при ускоренном движении жидкости профиль делается более полным (коэффициент 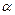уменьшается), а при замедленном - более вытянутым ( 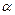увеличивается).

Дата добавления: 2014-10-31