Трубопроводов. Параллельное соединение простых

Параллельное соединение простых

Такое соединение нескольких простых трубопроводов (например 1, 2 и 3) между точками М и N показано на рис.16.4, а.

Рис. 16.4. Параллельное соединение трубопроводов

Для простоты допустим, что трубопроводы расположены в горизонтальной плоскости. Обозначим полные напоры в точках М и. N соответственно через Н_М и Н_N расход в основной магистрали (т. е. до разветвления и после слияния) через Q, а в параллельных трубопроводах через Q₁, Q₂ и Q₃; суммарные потери напора в этих трубопроводах через ∑ h₁, ∑ h₂, ∑ h₃.

Запишем следующее очевидное уравнение

Q = Q₁ + Q₂ + Q₃. (16.10)

Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N:

∑h₁ = H_M – H_N; ∑h₂ = H_M – HN; ∑h₃ = H_M – H_N.

Отсюда делаем следующий важный вывод:

∑h₁ =∑h₂ =∑h_{3 ,} (16.11)

т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом

∑h₁ = K1Q₁^m, ∑h₂ = K₂Q₂^m; ∑h3 = K₃Q₃^m,

где К и m - определяются в зависимости от режима течения формулами (16.3) или (16.4).

Следовательно, в дополнение к уравнению (16.10) получаем на основании равенств (16.11) еще два уравнения:

K₁Q₁^m = K₂Q₂^m; (16.12)

K₂Q₂^m = K₃Q₃^m. (16.13)

Система уравнений (16.10), (16.12) и (16.13) позволяет решать, например, следующую типичную задачу: даны расход в основной магистрали Q и все размеры трубопроводов; определить расходы в параллельных трубопроводах Q₁, Q₂ и Q₃. Пользуясь выражениями (16.10) и (16.11), можно составить столько уравнений, сколько параллельных трубопроводов между точками М и N.

Из уравнений (16.10) и (16.11) вытекает следующее важное правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах (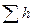). Пример такого построения дан на рис. 16.4, б.

Изложенные соотношения и правила для параллельных трубопроводов справедливы, разумеется, также в том случае, когда трубопроводы 1, 2, 3 и т. д. (см. рис. 16.4) не сходятся в одной точке N.

16.5. Разветвлённое соединение простых

Дата добавления: 2014-10-31