Основы расчета газопроводов

При установившемся движении вязкого газа по трубе постоянного сечения в силу постоянства вдоль потока массового расхода Q_m можно записать:

(вдоль потока) (17.9)

Так как движение газа сопровождается трением, давление его падает вдоль потока, газ расширяется, следовательно, плотность его уменьшается, а скорость , как это видно из формулы (17.9), увеличивается.

При полном отсутствии теплообмена с внешней средой процесс расширения при движении газа будет адиабатным, а при интенсивном теплообмене температура газа вдоль трубы остается постоянной, то есть происходит изотермический процесс. Чем короче газопровод и, следовательно, чем меньше время прохождения его частицами газа, тем ближе процесс к адиабатному. И наоборот, чем больше относительная длина газопровода, тем ближе процесс к изотермическому. Именно его и будем предполагать в газопроводах и рассмотрим основу их расчета применительно к изотермическому движению газа в трубах.

Выразим число Рейнольдса для потока газа в трубе через массовый расход газа и динамическую его вязкость

. (17.10)

Число Рейнольдса может изменяться вдоль потока в трубе постоянного диаметра лишь за счет изменения вязкости 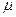. Но вязкость газов 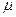не зависит от давления, а определяется лишь температурой, поэтому при изотермическом процессе движения газа по трубе число Рейнольдса будет оставаться постоянным вдоль потока. Следовательно, коэффициент потерь на трение по длине так же будет величиной постоянной вдоль трубы постоянного диаметра, несмотря на возрастания скорости потока газа.

Двумя бесконечно близкими друг к другу сечениями выделим элемент трубы длиной dx (рис. 17.4). Пренебрегая неравномерностью распределения скоростей по сечению, обозначим скорость в левом сечении трубы , в правом , а давления - соответственно и .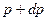

Рис. 17.4. Схема для расчета газопровода.

Применим к выделенному элементарному объему теорему механики об изменении количества движения. Приращение за единицу времени количества движения в направлении потока будет равно

, (17.11)

где .

Это приращение получается в результате импульса внешних сил: давления и трения за ту же единицу времени. Секундный импульс равнодействующей силы составит

,

где - касательное напряжение на стенке трубы.

Приравнивая секундный импульс сил приращению количества движения, получаем

или

. (17.12)

Поскольку , уравнение (17.12) можно записать в виде

. (17.13)

Умножив уравнение (17.13) на , будем иметь

. (17.14)

Согласно уравнению (17.9) , тогда

,

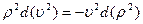и уравнение (17.14) можно переписать в виде

. (17.15)

Используя уравнения состояния , вместо выражения (17.15) получим

. (17.16)

Так как по условию T = const, можно выполнить интегрирование вдоль газопровода, т.е. в пределах от до и соответственно от x = 0 до х = 1. Будем иметь

(17.17)

Отсюда определяем массовый расход газа

(17.18)

В длинных трубопроводах при движении газа со скоростями, значительно меньшими звуковых,

В этих условиях выражением 2ln(p₁/p) в формуле (17.18) можно пренебречь и получить упрощенную формулу

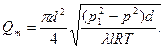(17.19)

Коэффициент λ, входящий в формулы (17.18) и (17.19), определяется так же, как и для несжимаемых жидкостей по числу Re и относительной шероховатости.

С помощью формулы (17.9), а также уравнения состояния и уравнения изотермы исключим из формулы (17.17) давления, введя в нее скорости, и приведем ее к виду

(17.20)

Полученное уравнение перепишем в безразмерных величинах; вводя отношение скорости потока к скорости звука, т.е. число Маха

(17.21)

где χ - известный из термодинамики показатель адиабаты, для воздуха и двухатомных газов χ = 1,4.

Тогда вместо выражения (17.20) будем иметь

(17.22)

Продифференцировав уравнение (17.22) по М и считая М₁ = const, получим

(17.23)

Анализируя это уравнение, приходим к выводу, что в случае изотермического течения при значении М² < 1/χ в цилиндрической трубе скорость вдоль потока возрастает (при и dМ > 0), а при значениях M² > 1/χ скорость вдоль потока уменьшается. Следовательно, значение для изотермического движения газа в трубе является критическим.

ЗАКЛЮЧЕНИЕ

Данный конспект лекций содержит сведения о физическом строении и основных физических свойствах жидкостей и газов, наиболее распространенных моделях их представления и описания. Применительно к жидкостям и газам рассмотрены основы кинематики сплошных сред, общие законы и уравнения статики и динамики, а также их применение к различным частным случаям движения и покоя.

Последовательное изложение учебного материала должно способствовать глубокому усвоению студентами дисциплины «Гидравлика». Применение основных физических закономерностей к частным случаям движения жидкостей и газов позволяет на конкретных примерах наиболее подробно изучить их специфические особенности.

Данная работа не охватывает всего курса дисциплины «Гидравлика (механика жидкости и газа)» и предназначена для восполнения имеющегося пробела в методической литературе, связанного с необходимостью системного изложения учебного материала в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования и примерной программы дисциплины, рекомендуемой министерством образования Российской Федерации для направления подготовки 151000 «Конструкторско- технологическое обеспечение автоматизированных машиностроительных производств», специальности 15100165 «Технология машиностроения».

Дата добавления: 2014-10-31