Местные сопротивления при ламинарном течении

При ламинарном режиме, во-первых, местные сопротивления обычно играют малую роль по сравнению с сопротивлением трения и, во-вторых, закон сопротивления является более сложным и исследован в меньшей степени, чем при турбулентном течении.

Если при турбулентном течении местные потери напора можно считать пропорциональными скорости (расходу) во второй степени, а коэффициенты потерь 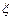определяются в основном формой местного сопротивления и практически не зависят от Re, то при ламинарном течении потерю напора 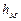следует рассматривать как сумму

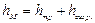, (13.11)

где 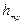- потеря напора, обусловленная непосредственным действием сил трения (вязкости) в данном местном сопротивлении и пропорциональная вязкости жидкости и скорости в первой степени;

- потеря, связанная с отрывом потока и вихреобразованием в самом местном сопротивлении или за ним и пропорциональная скорости во второй степени.

Так, при течении жидкости через жиклер (рис. 13.3) слева от плоскости расширения возникает потеря напора на трение, а справа - на вихреобразование.

Рис. 13.3. Схема жиклера

Учитывая закон сопротивления при ламинарном течении с поправкой на начальный участок, выражение (13.11) можно представить в виде

, (13.12)

где А и В - безразмерные константы, зависящие в основном от формы местного сопротивления.

После деления уравнения (13.12) на скоростной напор получим общее выражение для коэффициента местного сопротивления при ламинарном течении в трубопроводе:

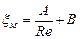. (13.13)

Соотношение между первым и вторым членами в формулах (13.12) и (13.13) зависит от формы местного сопротивления и числа Re. В местных сопротивлениях, где имеется узкий канал, длина которого значительно превышает его поперечный размер, с плавными очертаниями входа и выхода, а числа Re малы, потеря напора определяется в основном трением, и закон сопротивления близок к линейному. Второй член в формулах (13.12) и (13.13) в этом случае равен нулю или очень мал по сравнению с первым.

Если в местном сопротивлении трение сведено к минимуму, например, благодаря острой кромке, и имеются отрывы потока и вихреобразование, а числа Re достаточно велики, то потери напора пропорциональны скорости (и расходу) приблизительно во второй степени.

При широком диапазоне изменения числа Re в местном сопротивлении возможны как линейный (при малых Re), переходный (при средних Re), так и квадратичный (при больших Re) законы сопротивления.

Так при внезапном расширении русла при малых Re (Re < 9) коэффициент потерь слабо зависит от соотношения площадей и в основном определяется числом Re по формуле вида . При 9 < Re < 3500 коэффициент потерь зависит как от числа Re, так и от соотношения площадей. При Re > 3500 вполне справедлива теорема Борда.

Иногда вместо двучленной формы выражения местных гидравлических потерь применяют степенной одночлен:

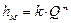, (13.14)

где k - размерная величина;

m - показатель степени, зависящий от формы местного сопротивления и Re и изменяющийся в пределах от 1 до 2.

Для местных сопротивлений и Re, при которых закон сопротивления близок к линейному, часто применяют выражение местных гидравлических потерь через эквивалентные длины l_экв трубопровода, т.е. фактическую длину l_фак трубопровода увеличивают на длину, эквивалентную по своему сопротивлению местным сопротивлениям. Таким образом,

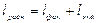; (13.15)

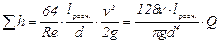. (13.16)

Численные значения эквивалентных длин (отнесенных к диаметру трубопровода) для различных местных сопротивлений обычно находят опытным путем.

Дата добавления: 2014-10-31