Внезапное расширение русла

Значения коэффициентов местных потерь в большинстве случаев получают из опытов, на основании которых выводят эмпирические формулы или строят графики. Однако для внезапного расширения русла при турбулентном течении потерю напора можно достаточно точно найти теоретическим путем.

При внезапном расширении русла (рис. 13.1) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. При этом, как показывают наблюдения, происходит непрерывный обмен частицами жидкости между основным потоком и завихренной его частью.

Рис. 13.1. Внезапное расширение трубы

Кроме того, основной вихрь порождает другие, более мелкие вихри, которые уносятся потоком и при этом распадаются на еще более мелкие вихри. Таким образом, потеря энергии происходит не только в основном вихре, но и по длине следующего за ним участка потока.

Рассмотрим два сечения горизонтального потока: 1-1 - в плоскости расширения трубы и 2-2 -в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту, на 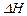большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на h_расш Эта высота и есть местная потеря напора на расширение.

Обозначим давление, скорость и площадь потока в сечении 1-1 соответственно через , а в сечении 2-2 - через 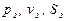_. Прежде чем составлять исходные уравнения, сделаем три допущения:

1) распределение скоростей в сечениях 1-1 и 2-2 равномерное; т.е. α₁ = α₂ = 1, что обычно и принимается при турбулентном режиме;

2) касательное напряжение на стенке трубы между сечениями 1-1 и 2-2 равно нулю, т.е. пренебрегаем силой трения, малой по сравнению с силами давления;

3) давление p₁ в сечении 1-1 действует по всей площади S₁ потому, что, хотя труба и расширилась, поток в сечении 1-1 еще сохранил свой поперечный размер, следовательно, ни скорость, ни давление еще не изменились.

Запишем для сечений 1-1 и 2-2 уравнение Д.Бернулли с учетом потери напора h_расш на расширение, и принимая z₁ = z₂ = 0, получим

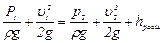. (13.2)

Затем применим теорему Эйлера об изменении количества движения к фиксированному цилиндрическому объему, заключенному между сечениями 1-1, 2-2 и стенкой трубы. Для этого определим равнодействующую внешних сил, действующих на рассматриваемый объем в направлении движения, т.е. сил давления. Учитывая, что площади оснований цилиндра слева и справа одинаковы и равны S₂ а также считая, что в сечении 1-1 давление p₁ равномерно распределено по всей площади S₂, получим равнодействующую силу, численно равную секундному импульсу . Соответствующее этому импульсу изменение количества движения найдем как разность между секундным количеством движения, выносимым из рассматриваемого объема и вносимым в него; при равномерном распределении скоростей по сечениям эта разность равна . Приравнивая одно к другому, получим:

=. (13.3)

Разделим полученное уравнение на 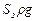; учитывая, что 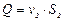, правая часть уравнения преобразуется к виду

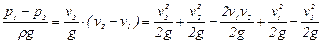. (13.4)

Сгруппировав члены, получим:

. (13.5)

Сравнение уравнения (13.5) с ранее записанным уравнением Д. Бернулли (13.2) показывает полную их аналогию, откуда делаем вывод, что

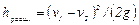, (13.6)

т.е. потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей. Это положение часто называют теоремой Борда в честь французского ученого, который в 1766 г. вывел эту формулу.

Если учесть, что согласно уравнению расхода , то полученный результат можно записать еще в виде, соответствующем общему способу выражения местных потерь:

, (13.7)

следовательно, для внезапного расширения русла коэффициент потерь равен:

. (13.8)

Доказанная теорема, как и следовало ожидать, хорошо подтверждается опытом при турбулентном течении и широко используется в расчетах.

Когда площадь S₂ весьма велика по сравнению с площадью S₁ и, следовательно, скорость 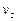можно считать равной нулю, потеря напора на расширение составляет 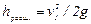, т.е. в этом случае теряется весь скоростной напор (вся кинетическая энергия, которой обладает жидкость); при этом коэффициент потерь 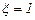. Такому случаю соответствует, например, подвод жидкости по трубе к резервуару достаточно больших размеров.

Рассмотренная потеря напора (энергии) при внезапном расширении русла расходуется, можно считать, исключительно на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание непрерывного вращательного движения жидких масс с постоянным их обновлением (обменом). Поэтому этот вид потерь энергии, пропорциональных скорости (расходу) во второй степени, называют потерями на вихреобразование. В конечном счете они расходуются на работу сил трения, но не непосредственно, как в прямых трубах постоянного сечения, а через вихреобразование.

Дата добавления: 2014-10-31