Ламинарное течение в круглых трубах

ЛЕКЦИЯ №11

Ламинарное течение является строго упорядоченным слоистым течением без перемешивания жидкости. Теория ламинарного течения основывается на законе вязкого трения между слоями движущейся жидкости (законе Ньютона-Петрова), которое в данном случае является единственным источником потерь энергии.

Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром . Чтобы исключить влияние силы тяжести и этим упростить вывод, допустим, что труба расположена горизонтально. Достаточно далеко от входа в нее, где поток уже вполне сформировался (стабилизировался), выделим отрезок длиной l между сечениями 1-1 и 2-2 (рис. 11.1).

Рис. 11.1. Схема к расчету ламинарного течения жидкости

в круглой трубе

Пусть в сечении 1-1 давление равно , а в сечении 2-2 -. Ввиду постоянства диаметра трубы, скорость жидкости будет постоянной, а коэффициент 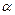будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Д. Бернулли для выбранных сечений примет вид

, (11.1)

где - потеря напора на трение по длине.

Преобразуя выражение (11.1) получаем:

, (11.2)

что и показывают пьезометры, установленные в этих сечениях.

В потоке жидкости выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т.е. равенство нулю суммы сил, действующих на объем: сил давления и сопротивления. Обозначая касательное напряжение на боковой поверхности цилиндра через 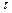, получим

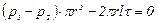, (11.3)

откуда . (11.4)

Из формулы следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюра касательного напряжения показана на рис. 11.1 слева (эта эпюра не зависит от режима течения).

Выразим касательное напряжение 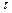по закону вязкого трения Ньютона через динамическую вязкость и поперечный градиент скорости:

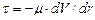. (11.5)

Знак минус обусловлен тем, что направление отсчета r принято от оси к стенке. Подставляя значение 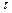в предыдущее уравнение, получаем:

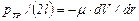. (11.6)

Найдем отсюда приращение скорости

. (11.7)

При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рис. 11.1.

Выполнив интегрирование, получим

. (11.8)

Постоянную интегрирования С найдем из условия, что на стенке при V = 0:

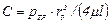. (11.9)

Скорость по окружности радиусом r

. (11.10)

Это выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении (законом Стокса). Кривая, изображающая эпюру скоростей, является параболой второй степени.

Максимальная скорость, имеющая место в центре сечения (при r = 0), будет равна

. (11.11)

Входящее в формулу отношение 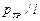(см. рис. 11.1) представляет собой гидравлический (пьезометрический) уклон, умноженный на 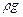. Эта величина является постоянной вдоль прямой трубы постоянного диаметра.

Применим полученный закон распределения скоростей, описываемый уравнением (11.10), для расчета расхода. Для этого выразим сначала элементарный расход через бесконечно малую площадку dS:

. (11.12)

Здесь V есть функция радиуса, определяемая формулой (11.10), а площадку dS целесообразно взять в виде кольца радиусом r и шириной dr, тогда

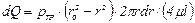. (11.13)

После интегрирования по всей площади поперечного сечения, т.е. от до получаем:

, (11.14)

Среднюю по сечению скорость найдем делением расхода на площадь. С учетом выражения (11.14) получим:

. (11.15)

Cравнениe этого выражения с формулой (11.11) показывает, что средняя скорость пpи ламинарном течении в 2 pаза меньше максимальной: .

Для получения закона сопротивления, т.е. выражения потери напора на трение через расход и размеры трубы, определим из формулы (11.14):

. (11.16)

Разделив это выражение на 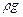, заменив 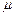на и на 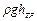, а так же перейдя от 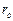к , найдем:

. (11.17)

Полученный зaкон сопротивления показывает, что при ламинарном течении в трубе круглого сечения потеря напора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, обычно называемый законом Пуазейля, который впервые получил его экспериментальным путем, используется для расчета трубопроводов с ламинарным течением.

Преобразуем выражение (11.17) с учетом уравнения (11.15) следующим образом:

, (11.18)

или, обозначая - коэффициент потерь на трение для ламинарного течения, окончательно получим:

. (11.19)

Формула (11.19) носит название формулы Дарси-Вейсбаха и выражает закон сопротивления трения по длине трубопровода при ламинарном течении жидкости. Зная закон распределения скоростей по сечению трубы, легко определить коэффициент Kopиолиса 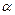, учитывающий неравномерность распределения скоростей в уравнении Д. Бернулли, для случая стабилизированного ламинарного течения жидкости в круглой трубе. Для этого в выражении (10.7) заменим скорость по формуле (11.10) и среднюю скорость по формуле (11.15), a также учтем, что S = πr²₀ и dS = 2πrdr. Послe подстановок и сокращений получим:

.

Итак, действительно кинетическая энергия ламинарного потока с параболическим распределением скоростей в 2 раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.

Таким же путём можно показать, что секундное количество движения ламинарного потока с параболическим распределением скоростей в 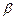раз больше количества движения того же потока, но при равномерном распределении скоростей, причем коэффициент 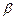, называемый коэффициентом Буссинесска, в данном случае равен 4/3.

Изложенная теория ламинарного течения жидкости в круглой трубе подтверждается опытом, и выведенный закон сопротивления обычно не нуждается в каких-либо поправках, за исключением следующих случаев:

1) при течении в начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей;

2) при течении с теплообменом;

3) при течении в капиллярах и зазорах с облитерацией;

4) при течении с большими перепадами давления.

Дата добавления: 2014-10-31