Нахождение координат точки, лежащей на прямой, по которой пересекаются две плоскости

Сначала рассмотрим следующую задачу. Пусть прямоугольной системе координат Oxyz в трехмерном пространстве прямая a задана уравнениями двух пересекающихся плоскостей как и дана точка трехмерного пространства 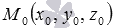. Требуется определить, принадлежит ли точка M₀ заданной прямой a.

Для решения поставленной задачи нужно подставить координаты точки 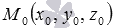в каждое из двух уравнений, соответствующих пересекающимся плоскостям. Если при этом получим два верных равенства 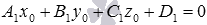и 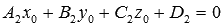(это будет означать, что точа М₀ принадлежит и плоскост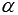и и 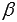), то точка М₀ принадлежит заданной прямой. Если хотя бы одно из равенств 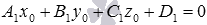или 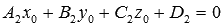неверно, то точка М₀ не лежит на прямой a.

Пример. Лежат ли точк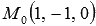и и 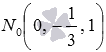на прямой, заданной в пространстве уравнениями двух пересекающихся плоскостей .

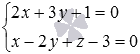Решение. Подставим координаты точки М₀ в уравнения системы: 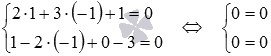. При этом получаем два верных равенства, следовательно, точка 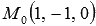лежит на заданной прямой.

Теперь подставляем координаты точки N₀: 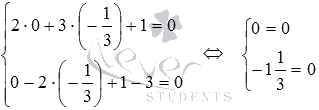. Второе уравнение системы обратилось в неверное равенство, поэтому, точка 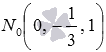не лежит на заданной прямой.

Ответ. Точка М₀ лежит на прямой, а N₀ не лежит.

Теперь рассмотрим задачу нахождения координат некоторой точки, лежащей на прямой, если прямая в пространстве в прямоугольной системе координат определяется уравнениями пересекающихся плоскостей .

Решением этой задачи является любое из бесконечного множества решений системы из двух линейных уравнений с тремя неизвестными вида .

Пример. Найдите координаты любой точки прямой, заданной в пространстве уравнениями двух пересекающихся плоскостей .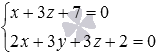

Решение. Перепишем систему уравнений в следующем виде

В качестве базисного минора основной матрицы системы возьмем отличный от нуля минор второго порядка 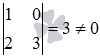, то есть, z – свободная неизвестная переменная. Перенесем слагаемые, содержащие z, в правые части уравнений: .

Примем 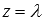, где 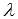- произвольное действительное число, тогда .

Решим полученную систему уравнений методом Крамера:

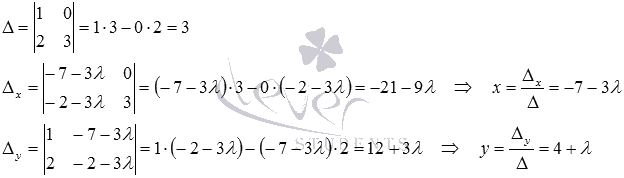
Таким образом, общее решение системы уравнений 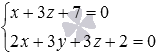имеет вид 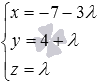, где .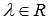

Если взять конкретное значение параметра 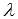, то мы получим частное решение системы уравнений, которое нам дает искомые координаты точки, лежащей на заданной прямой. Возьмем 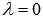, тогда 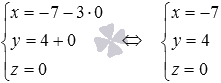, следовательно, 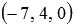- искомая точка прямой.

Можно выполнить проверку найденных координат точки, подставив их в исходные уравнения двух пересекающихся плоскостей:

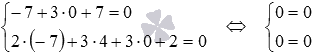
Ответ. .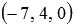

Дата добавления: 2014-10-31