
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Переход от параметрических уравнений прямой в пространстве к другим видам уравнений прямой
|
|
|
|
Существуют различные виды уравнений прямой в пространстве. В зависимости от условий решаемой задачи, которая связана с прямой линией в прямоугольной системе координат в пространстве, иногда приходится переходить от одного вида уравнений прямой к другому.
Сейчас мы покажем как из параметрических уравнений прямой 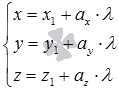 получить канонические уравнения прямой в пространстве вида
получить канонические уравнения прямой в пространстве вида 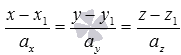 и уравнения двух пересекающихся плоскостей вида
и уравнения двух пересекающихся плоскостей вида 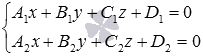 , определяющих заданную прямую.
, определяющих заданную прямую.
Получить канонические уравнения прямой в заданной прямоугольной системе координат в пространстве при известных параметрических уравнениях прямой не представляет сложности. Для этого нужно разрешить каждое из параметрических уравнений прямой относительно параметра 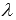 и приравнять правые части полученных равенств:
и приравнять правые части полученных равенств:
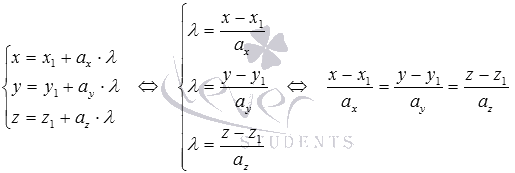
Пример. Перейдите от параметрических уравнений прямой 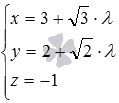 к каноническим уравнениям прямой в заданной прямоугольной системе координат Oxyz в трехмерном пространстве.
к каноническим уравнениям прямой в заданной прямоугольной системе координат Oxyz в трехмерном пространстве.
Решение. Перепишем исходные параметрические уравнения прямой в виде 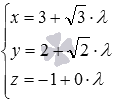 . Разрешим каждое из них относительно параметра и приравняем правые части полученных равенств:
. Разрешим каждое из них относительно параметра и приравняем правые части полученных равенств:
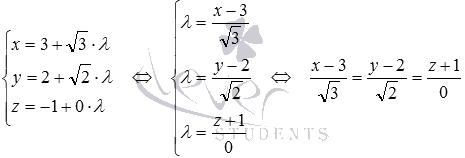
Ответ. 
Теперь давайте разберемся, как получить уравнения двух пересекающихся плоскостей, которые бы задавали прямую, соответствующую параметрическим уравнениям прямой вида 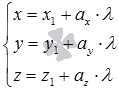 .
.
Начнем с самых простых случаев.
Если  , то параметрические уравнения прямой имеют вид
, то параметрические уравнения прямой имеют вид 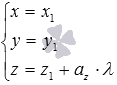 . В этом случае очевидно, что прямая является линией пересечения плоскостей
. В этом случае очевидно, что прямая является линией пересечения плоскостей  и
и 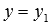 .
.
Аналогично, если 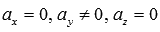 , то параметрические уравнения прямой
, то параметрические уравнения прямой  задают прямую линию, по которой пересекаются две плоскости
задают прямую линию, по которой пересекаются две плоскости  и
и 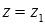 . При
. При  , прямая
, прямая  задается двумя пересекающимися плоскостями
задается двумя пересекающимися плоскостями 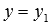 и
и 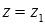 .
.
Пример. Напишите уравнения двух плоскостей, которые пересекаются по прямой, заданной в прямоугольной системе координат Oxyz в пространстве параметрическими уравнениями  .
.
Решение. Из заданных параметрических уравнений прямой мы можем сразу записать уравнения двух пересекающихся плоскостей, определяющих эту прямую:  .
.
Ответ. 
Переходим к следующим случаям.
Если 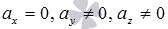 , то параметрические уравнения прямой примут вид
, то параметрические уравнения прямой примут вид 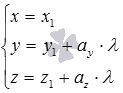 . Уравнение первой плоскости очевидно -
. Уравнение первой плоскости очевидно -  . Для получения второго уравнения плоскости нужно разрешить второе и третье параметрические уравнения относительно параметра
. Для получения второго уравнения плоскости нужно разрешить второе и третье параметрические уравнения относительно параметра 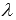 и приравнять правые части:
и приравнять правые части:

Аналогично поступаем, если 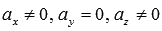 или
или 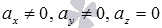 .
.
Пример. Получите уравнения двух плоскостей, которые пересекаются по прямой, определяемой в прямоугольной системе координат Oxyz в трехмерном пространстве параметрическими уравнениями  .
.
Решение. Уравнение первой плоскости очевидно:  . Уравнение второй плоскости получим, отталкиваясь от первого и третьего параметрических уравнений прямой:
. Уравнение второй плоскости получим, отталкиваясь от первого и третьего параметрических уравнений прямой:

Ответ. 
Остался не рассмотрен один случай – когда 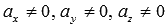 . При этом следует разрешить каждое параметрическое уравнение прямой относительно параметра
. При этом следует разрешить каждое параметрическое уравнение прямой относительно параметра 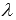 и попарно приравнять правые части:
и попарно приравнять правые части:
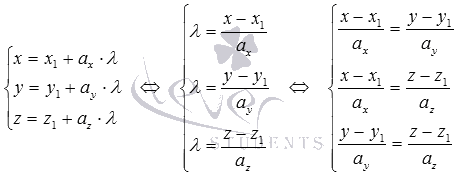
Тогда приходим к трем уравнениям пучка плоскостей с линией пересечения, определяемой параметрическими уравнениями прямой 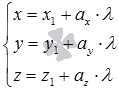 . Нам достаточно двух из трех уравнений плоскостей пучка.
. Нам достаточно двух из трех уравнений плоскостей пучка.
Пример. Напишите уравнения двух пересекающихся плоскостей, определяющих прямую линию, которая в прямоугольной системе координат Oxyz в трехмерном пространстве задана параметрическими уравнениями вида  .
.
Решение. Разрешим параметрические уравнения прямой относительно параметра 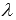 :
: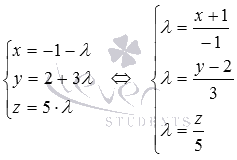
После попарного приравнивания правых частей равенств имеем

Берем любые два из трех полученных уравнений плоскостей.
Ответ. 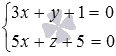
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 2003; Нарушение авторских прав?; Мы поможем в написании вашей работы!