Преобразование и построение Матриц

Пример 1.

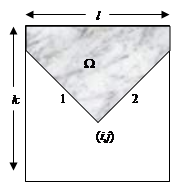
Пусть задана матрица A, размерностью n x n. Необходимо построить матрицу В, причем элементы матрицы строятся по следующей формуле 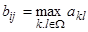, где область указана рисунке.

В задачах о выделении областей в матрицах необходимо научиться записывать уравнения изменения индексов при движении по линиям, параллельным главной диагонали, и по линиям, перпендикулярным диагонали.

Запишем уравнение линий (1) и (2), проходящих через фиксированную точку (i,j). Пусть изменяемые индексы – l и k. Тогда уравнение прямой (1) (см. рис.1) имеет вид: l = j – i + k, а прямая (2) описывается соотношением: l = j + i - k. Области изменения индексов показаны на рисунке. Если необходимо описать заштрихованную область, то это следует делать так, как это делается при описании областей на плоскости. Легко видеть, что индекс k изменяется в пределах от 1 до i. Индекс l удовлетворяет неравенству 1 £ l £ n. Область выше линии (1) описывается неравенством l > j – i + k, а область выше линии (2) - l < j + i - k. Так как указанная область является пересечением указанных областей, то все перечисленные выше неравенства следует соединять в логическом выражении союзом «и». Таким образом, при построении матрицы В следует воспользоваться четырьмя вложенными циклами, где два внешних описывают индексы матрицы В, то есть изменяются от 1 до n. Что касается двух внутренних циклов, то индекс k изменяется от 1 до i, а индекс l изменяется в пределах от прямой (1) до прямой (2). Ограничения 0 и n следует внести в условие оператора if. Схематически структуру циклов можно изобразить так:

i =1 ¸ n

j =1 ¸ n

k = 1 ¸ i

l = j – i + k ¸ j + i – k

1 £ l £ n

Конец цикла по l

Конец цикла по k

Конец цикла по j

Конец цикла по i

Программа решения этой задачи и результаты ее выполнения представлены ниже.

#include <stdio.h>

#include <conio.h>

#define m 6

void main()

{ int i,j,k,l,n;

float a[m][m],b[m][m];

clrscr();

gotoxy(5,5); printf("ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ");

gotoxy(5,6); printf(" b(i,j)=max a(k,l), k,l принадлежат");

gotoxy(9,7); printf(" заштрихованной области");

gotoxy(35,10); printf("┌ ┐");

gotoxy(35,11); printf("│ * * * * * * * * * * * * * │");

gotoxy(35,12); printf("│ * * * * * * * * * * * * │");

gotoxy(35,13); printf("│ * * * * * * * * * * * │");

gotoxy(35,14); printf("│ * * * * * * * * * │");

gotoxy(35,15); printf("│ * * * * * * * │");

gotoxy(35,16); printf("│ * * * * * │");

gotoxy(35,17); printf("│ * * * │");

gotoxy(35,18); printf("│ * │");

gotoxy(35,19); printf("│ │");

gotoxy(35,20); printf("│ │");

gotoxy(35,21); printf("│ │");

gotoxy(35,22); printf("└ ┘");

getchar();clrscr();

do{

printf("\n\nВведите размерность матрицы <=%d ",m);

scanf("%d",&n);

}while(!(n>0 && n<=m));clrscr();

for (i=1;i<=n;i++)

for (j=1;j<=n;j++){

printf("Введите a(%d,%d)=",i,j);scanf("%f",&a[i-1][j-1]);

}

clrscr();

printf("ИСХОДНАЯ МАТРИЦА\n");

for (i=1;i<=n;i++){

for (j=1;j<=n;j++)

printf("%7.2f",a[i-1][j-1]);

printf("\n");

}

for (i=1;i<=n;i++)

for (j=1;j<=n;j++){

b[i-1][j-1]=-1.e20;

for (k=1;k<=n;k++)

for (l=j-i+k;l<=j+i-k;l++)

if (l>=1 && l<=n && a[k-1][l-1]>b[i-1][j-1])

b[i-1][j-1]=a[k-1][l-1];

}

printf("ПОЛУЧЕННАЯ МАТРИЦА\n");

for (i=1;i<=n;i++){

for (j=1;j<=n;j++)

printf("%7.2f",b[i-1][j-1]);

printf("\n");

}

getchar();getchar();

}

При выполнении данной программы на экране монитора будет выведено следующее:

ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ

b(i,j)=max a(k,l), k,l

принадлежат заштрихованной области

┌ ┐

│* * * * * * * * * * * * * │

│ * * * * * * * * * * * * │

│ * * * * * * * * * * * │

│ * * * * * * * * * │

│ * * * * * * * │

│ * * * * * │

│ * * * │

│ * │

│ │

│ │

│ │

└ ┘

Введите размерность матрицы <=6 4

Введите a(1,1)= 1.00

Введите a(1,2)= 4.00

Введите a(1,3)= 2.00

Введите a(1,4)= -3.60

Введите a(2,1)= 8.90

Введите a(2,2)= -22.10

Введите a(2,3)= 5.00

Введите a(2,4)= 0.78

Введите a(3,1)= -3.45

Введите a(3,2)= 2.40

Введите a(3,3)= 9.80

Введите a(3,4)= 6.12

Введите a(4,1)= -23.50

Введите a(4,2)= 1.00

Введите a(4,3)= 7.00

Введите a(4,4)= 89.00

ИСХОДНАЯ МАТРИЦА

1.00 4.00 2.00 -3.60

8.90 -22.10 5.00 0.78

-3.45 2.40 9.80 6.12

-23.50 1.00 7.00 89.00

ПОЛУЧЕННАЯ МАТРИЦА

1.00 4.00 2.00 -3.60

8.90 4.00 5.00 2.00

8.90 8.90 9.80 6.12

8.90 9.80 9.80 89.00

Пример 2.

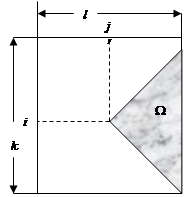
Пусть задана матрица A, размерностью n x n. Необходимо построить матрицу В, причем элементы матрицы строятся по следующей формуле 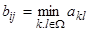, где область указана рисунке. Область в этом случае следует описать сначала по l, так как этот индекс изменяется в пределах от j до n. Следовательно, внутренние циклы будут: сначала по l от j до n, а затем цикл по k от j+i-l до l-j+i. Так как ищется минимум, то начальное значение следует выбрать достаточно большим. Текст программы и результаты ее работы представлены ниже.

#include <stdio.h>

#include <conio.h>

#define m 6

void main()

{ int i,j,k,l,n;

float a[m][m],b[m][m];

clrscr();

gotoxy(5,5);

printf("ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ");

gotoxy(5,6);

printf(" b(i,j)=min a(k,l), k,l принадлежат");

gotoxy(9,7);

printf(" заштрихованной области");

gotoxy(35,10); printf("┌ ┐");

gotoxy(35,11); printf("│ │");

gotoxy(35,12); printf("│ * │");

gotoxy(35,13); printf("│ * * │");

gotoxy(35,14); printf("│ * * * │");

gotoxy(35,15); printf("│ * * * * │");

gotoxy(35,16); printf("│ * * * * * │");

gotoxy(35,17); printf("│ * * * * * * │");

gotoxy(35,18); printf("│ * * * * * │");

gotoxy(35,19); printf("│ * * * * │");

gotoxy(35,20); printf("│ * * * │");

gotoxy(35,21); printf("│ * * │");

gotoxy(35,22); printf("│ * │");

gotoxy(35,23); printf("└ ┘");

getchar();clrscr();

do{

printf("\n\nВведите размерность матрицы <=%d ",m);

scanf("%d",&n);

}while(!(n>0 && n<=m));clrscr();

for (i=1;i<=n;i++)

for (j=1;j<=n;j++){

printf("Введите a(%d,%d)=",i,j);scanf("%f",&a[i-1][j-1]);

}

clrscr();

printf("ИСХОДНАЯ МАТРИЦА\n");

for (i=1;i<=n;i++){

for (j=1;j<=n;j++)

printf("%7.2f",a[i-1][j-1]);

printf("\n"); }

for (i=1;i<=n;i++)

for (j=1;j<=n;j++){

b[i-1][j-1]=1.e20;

for (l=j;l<=n;l++)

for (k=j+i-l;k<=l-j+i;k++)

if (k>=1 && k<=n && a[k-1][l-1]<b[i-1][j-1])

b[i-1][j-1]=a[k-1][l-1]; }

printf("ПОЛУЧЕННАЯ МАТРИЦА\n");

for (i=1;i<=n;i++){

for (j=1;j<=n;j++)

printf("%7.2f",b[i-1][j-1]);

printf("\n"); }

getchar();getchar();}

При выполнении данной программы на экране монитора будет выведено следующее:

ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ

b(i,j)=min a(k,l), k,l принадлежат заштрихованной области

┌ ┐

│ │

│ * │

│ * * │

│ * * * │

│ * * * * │

│ * * * * * │

│ * * * * * * │

│ * * * * * │

│ * * * * │

│ * * * │

│ * * │

│ * │

└ ┘

Введите размерность матрицы <=6 4

Введите a(1,1)= 2.50

Введите a(1,2)= 3.80

Введите a(1,3)=-2.28

Введите a(1,4)= 4.00

Введите a(2,1)= 6.21

Введите a(2,2)= 9.80

Введите a(2,3)=-3.54

Введите a(2,4)= 6.00

Введите a(3,1)= 1.34

Введите a(3,2)= 6.80

Введите a(3,3)=-2.13

Введите a(3,4)= 5.00

Введите a(4,1)= 4.00

Введите a(4,2)= 8.12

Введите a(4,3)= 5.00

Введите a(4,4)= 3.00

ИСХОДНАЯ МАТРИЦА

2.50 3.80 -2.28 4.00

6.21 9.80 -3.54 6.00

1.34 6.80 -2.13 5.00

4.00 8.12 5.00 3.00

ПОЛУЧЕННАЯ МАТРИЦА

-3.54 -3.54 -2.28 4.00

-3.54 -3.54 -3.54 6.00

-3.54 -3.54 -2.13 5.00

-3.54 -2.13 3.00 3.00

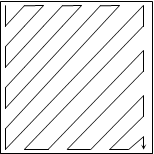Пример 3. Дан одномерный массив целых чисел Р размерностью 64. Получить квадратную матрицу порядка 8,элементами которой являются числа массива Р, расположенные в ней по схеме, приведенной на рисунке.

Эта задача решается с помощью одного основного цикла, в котором организуется управление изменением индексов в зависимости от условий размещения элементов. Для отслеживания направления движения по диагонали вводится вспомогательная переменная l. Ее значение равно 0 при движении вниз по диагонали и 1 при движении вверх.

#include<stdio.h>

#include<math.h>

#include<conio.h>

void main()

{ clrscr();

float p[64];

float a[8][8];

int n=8,i=0,j=0,k,l=0;

for (k=0;k<n*n;k++)

p[k]=k;

for (k=0;k<n*n;k++)

{ a[i][j]=p[k];

if (j==0 && i<n-1 && l==0)

{ i++;l=1; }

else if (i==0 && j<n-1 && l==1)

{ j++; l=0;}

else if (j==n-1 && l==1)

{ i++;l=0; }

else if (i==n-1 && l==0)

{ j++; l=1;}

else if (l==0)

{ i++; j--;}

else

{ i--; j++; }

}

for (i=0;i<n;i++)

{ for (j=0;j<n;j++)

printf("%3.0f ",a[i][j]);

printf ("\n");

}

}

Дата добавления: 2014-10-31