Два замечательных предела

В этом разделе приводятся два предела функции, которые наиболее широко используются в математике и ее приложени­ях. Доказательства соответствующих теорем мы опускаем.

ТЕОРЕМА 4. Предел функции 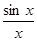в точке х = 0 существу­ет и равен единице, т.е.

Предел (3.7) называется первым замечательным пределом. Этот предел применяется при вычислении ряда других преде­лов. Рассмотрим несколько примеров на применение предела (3.7).

Пример 1. Найти предел функции sin (ax) / bx при х 0.

Решение. Преобразуем данную дробь так, чтобы в знаме­нателе был аргумент синуса; только тогда можно будет при­менить первый замечательный предел, поскольку при х 0 пределом ах также является нуль. Получаем

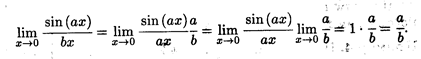
Пример 2. Найти .

Решение. Теорему 3.2 здесь непосредственно применить нельзя, так как при х 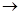0 знаменатель дроби стремится к нулю. Для решения задачи необходимо сначала преобразовать данную дробь, а затем уже выполнить предельный переход:

Пример 3. Найти .

Решение. Как и в первых двух примерах, преобразуем данную дробь, чтобы "подогнать" ее под первый замечательный предел:

ТЕОРЕМА 5 (второй замечательный предел). Предел функции f(x) = 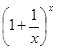при х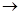 существует и равен е, т.е.

Число е является одной из фундаментальных величин в ма­тематике. Показательная функция вида е­­^ax называется экспонентой, логарифм с основанием е называется натуральным и обозначается символом ln. В теории вероятностей и статистике функция является основополагающей.

Второй замечательный предел (3.8) широко применяется для вычисления других пределов. Рассмотрим примеры на его применение.

Пример 4. Найти .

Решение. Применим здесь замену переменной, полаем 1/ x = у. Тогда у 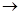при x 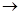0, т.е. имеем

Пример 5. Найти .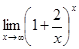

Решение. Заменим переменную, положив x = 2 у. При x 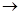(а значит, и у 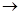) последовательно получаем

Пример 6. Найти .

Решение. Сначала преобразуем дробь под знаком предела, а затем уже перейдем к пределу:

Дата добавления: 2014-10-15