Часть 7. Принятие решений и элементы планирования

Глава 31. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР

В экономике иногда приходится сталкиваться с ситуацией, когда при наличии многих участников эффективность реше­ния одного из них зависит от того, какие решения приняли другие участники. Например, доход предприятия от продажи изделия зависит не только от установленной на него цены, но и от количества купленных покупателем изделий. Или при вы­боре ассортимента товаров, выпускаемых предприятием, нуж­но учитывать, какой ассортимент товаров выпускают другие предприятия.

Все ситуации, когда эффективность действия одного из участников зависит от действий других, можно разбить на два типа: интересы участников совпадают, и они могут догово­риться о совместных действиях; интересы участников не сов­падают. В этом случае может оказаться невыгодным сообщать другим участникам свои решения, так как кто-нибудь из них сможет воспользоваться знанием чужих решений и получит больший выигрыш за счет других участников. Ситуации та­кого типа называются конфликтными. Построением матема­тических моделей конфликтных ситуаций и разработкой мето­дов решения возникающих в этих ситуациях задач занимается теория игр.

В игре могут сталкиваться интересы двух или нескольких противников, поэтому игры разделяются на парные и множес­твенные. Если во множественной игре интересы игроков сов­падают, то они могут объединяться, создавая коалиции. Такие игры называются коалиционными.

Задачей теории игр является выработка рекомендаций для игроков, т.е. определение для них оптимальной стратегии. Стратегией игрока называется система правил, однозначно определяющих поведение игрока на каждом ходе в зависимос­ти от ситуации, сложившейся в процессе игры. Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш. Количество стратегий у каждого игрока может быть конечным или бесконечным, в зависимости от это­го игры подразделяются на конечные и бесконечные.

Рассмотрим простейшую математическую модель конеч­ной конфликтной ситуации, когда имеются два участника и когда выигрыш одного равен проигрышу другого. Такая мо­дель называется антагонистической игрой двух лиц с нулевой суммой.

В игре участвуют первый и второй игроки, каждый из них может записать независимо от другого цифры 1, 2 и 3. Ес­ли разность между цифрами, записанными игроками, положи­тельна, то первый игрок выигрывает количество очков, равное разности между цифрами, и, наоборот, если разность отрица­тельна, то выигрывает второй игрок. Если разность равна ну­лю, то игра заканчивается вничью.

У первого игрока три стратегии (варианта действия): А ₁(записать 1), А ₂ (записать 2), А ₃ (записать 3); у второго игрока также три стратегии: B ₁, B ₂, В ₃ (табл. 33.1).

Задача первого игрока — максимизировать свой выигрыш. Задача второго игрока — минимизировать свой проигрыш или минимизировать выигрыш первого игрока.

Игру можно представить в виде матрицы, в которой стро­ки — стратегии первого игрока, столбцы — стратегии второго игрока, а элементы матрицы — выигрыши первого игрока. Та­кую матрицу называют платежной.

Для данного примера платежная матрица имеет вид

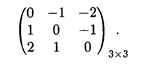
В общем случае парную игру с нулевой суммой можно за­писать платежной матрицей

Задача каждого из игроков — найти наилучшую страте­гию игры, при этом предполагается, что противники одина­ково разумны и каждый из них делает все, чтобы получить наибольший доход.

Найдем наилучшую стратегию первого игрока: минималь­ное число а„ в каждой строке обозначим α _i (i = ),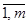

Зная α _i, т.е. минимальные выигрыши при различных стра­тегиях А_i, первый игрок выберет ту стратегию, для которой α _i максимально. Обозначим это максимальное значение через α, тогда

Величина α — гарантированный выигрыш, который может обеспечить себе первый игрок, — называется нижней ценой игры (максимином).

Аналогично для определения наилучшей стратегии второго игрока найдем максимальные значения выигрыша по столбцам и, выбрав из них минимальное значение, получим

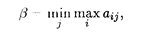
где β — верхняя цена игры (минимакс).

Если второй игрок будет придерживаться своей минимакс­ной стратегии, то он гарантирован, что в любом случае про­играет не больше β.

Для матричной игры справедливо неравенство

Если α = β, то такая игра называется игрой с седловой точ­кой, а пара оптимальных стратегий (А_{i опт}, B_{j опт}) — седловой точкой матрицы. В этом случае элемент α _ij = v называется ценой игры, является одновременно минимальным в i -й строке и j- м столбце. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.

Найдем решение игры рассмотренного выше примера:

Так как α = β = 0, матрица игры имеет седловую точку.

Оптимальная стратегия первого игрока — А ₃, второго — В ₃. Из табл. 31.1 видно, что отклонение первого игрока от оп­тимальной стратегии уменьшает его выигрыш, а отклонение второго игрока от В ₃ увеличивает его проигрыш.

Если платежная матрица не имеет седловой точки, т.е. α < β, то поиск решения игры приводит к применению слож­ной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами. Такая сложная стратегия называется смешанной.

В игре, матрица которой имеет размерность т х п, стра­тегии первого игрока задаются наборами вероятностей = (x ₁, x ₂ ,...,x_т), с которыми игрок применяет свои чистые стратегии. Эти наборы можно рассматривать как m -мерные векторы, для координат которых

Аналогично для второго игрока наборы вероятностей опре­деляют n -мерные векторы 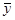= (y ₁, y ₂, …, y_п), для координат которых

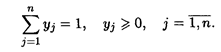
Выигрыш второго игрока при использовании смешанных стратегий определяют как математическое ожидание выигры­ша, т.е. он равен

В основной теореме теории игр утверждается, что каждая конечная игра имеет, по крайней мере, одно решение, возмож­но, в области смешанных стратегий.

Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: a ≤ v ≤ b.

Применение первым игроком оптимальной стратегии x_{i опт} должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соот­ношение

Аналогично второму игроку оптимальная стратегия y_{j опт}должна обеспечить при любых стратегиях первого игрока про­игрыш, не превышающий цену игры, т.е. справедливо соотно­шение

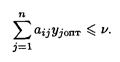
Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому матрицы большой раз­мерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и заведо­мо невыгодных стратегий. Рассмотрим игру, представленную платежной матрицей

Откуда имеем

Все элементы А ₂ меньше A ₃, т.е. А ₃ заведомо невыгодна для первого игрока и А ₂ можно исключить. Все элементы А ₄меньше А ₃, исключаем А ₄.

Для второго игрока: сравнивая В ₁ и B ₄, исключаем В ₁;сравнивая В ₂ и В ₄, исключаем В ₂; сравнивая B ₃ и В ₄, исклю­чаем В ₃. В результате преобразований получим матрицу

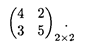
31.1. Графическое решение игр вида (2 x n) и (m x 2)

Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии. Рассмотрим игру (2 х п), см. табл. 31.2.

Предполагаем, что игра не имеет седловой точки.

Обозначим: х ₁ — вероятность применения первым игроком 1-й стратегии, x ₂ — вероятность применения первым игроком 2-й стратегии, причем х ₂ = 1 — x ₁; y ₁ — вероятность примене­ния вторым игроком 1-й стратегии, у ₂ — вероятность приме­нения вторым игроком 2-й стратегии и т.д., у_n — вероятность применения вторым игроком п -й стратегии.

Ожидаемый выигрыш первого игрока при применении вто­рым 1-й стратегии составит

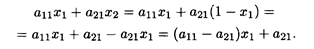
Аналогично найдем ожидаемые выигрыши первого игрока при применении вторым игроком 2, 3,..., n -й стратегий. Полу­ченные данные поместим в табл. 31.3.

Из таблицы видно, что ожидаемый выигрыш первого иг­рока линейно зависит от x ₁. На оси X ₁ построим выражения ожидаемых выигрышей первого игрока.

Первый игрок должен выбирать такие стратегии, чтобы максимизировать свой минимальный ожидаемый выигрыш. Поэтому оптимальная стратегия первого игрока определяется как точка пересечения прямых, максимизирующих его мини­мальный ожидаемый выигрыш.

Аналогично находим оптимальную стратегию второго иг­рока. Она определяется как точка пересечения прямых, мини­мизирующих его максимальные ожидаемые проигрыши.

Пример 1. Рассмотрим представленную выше игру, заданную платежной матрицей

Найти оптимальные стратегии игроков и цену игры.

Решение. Обозначим: x ₁ — вероятность применения пер­вым игроком 1-й стратегии, х ₂, х ₃, х ₄ — вероятность исполь­зования первым игроком 2, 3, 4-й стратегий соответственно, причем х ₁ + x ₂ + x ₃ + x ₄ = 1; y ₁ — вероятность применения вторым игроком 1-й стратегии, у ₂, у ₃, y ₄, y ₅ — вероятность использования вторым игроком 2, 3, 4, 5-й стратегий соответ­ственно, причем y ₁ + у ₂ + у ₃ + y ₄ + y ₅ = 1.

Платежная матрица была упрощена путем вычеркивания дублирующих, заведомо невыгодных стратегий. Поэтому x ₂ = x ₄ = y ₁ = y ₂ = y ₃ = 0 и матрица имеет вид

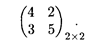
Найдем решение игры (табл. 31.4) графическим методом (рис. 31.1). На оси Х ₁ разместим точки х ₁ = 0 и х ₁ = 1, через которые проведем прямые, перпендикулярные оси Х ₁. Подстав­ляя х ₁ = 0 и x ₁ = 1 в выражение х ₁ +3, найдем значения, кото­рые отложим на соответствующих перпендикулярных прямых. Соединив эти точки, получим прямую.

Аналогично рассмотрим выражение –3 x ₁ + 5.

Оптимальная стратегия первого игрока определится из ра­венства выражений х ₁ + 3 и - 3 х ₁ + 5:

Цена игры v = x ₁ + 3 = 1/2 + 3 = 7/2.

Оптимальная стратегия первого игрока:

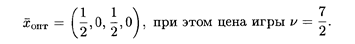
Найдем оптимальную стратегию для второго игрока (табл. 31.5).

Имеем

Оптимальная стратегия второго игрока (рис. 31.2):

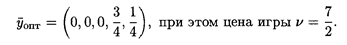
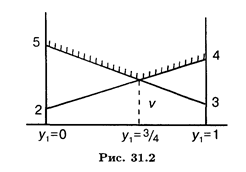
Пример 2. Найдем решение игры вида (2 х n), заданной пла­тежной матрицей (табл. 31.6)

Решение. Находим

α = mах (-1,2) = 2, β = min (4, 3, 3, 6) = 3, 2≤ v ≤ 3.

Тогда

Оптимальное решение первого игрока:

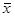_опт = (1/2, 1/2), при этом цена игры составляет v = 5/2.

Найдем оптимальное решение второго игрока (табл. 31.7).

Из рис. 31.3 следует, что оптимальная стратегия первого игрока определяется из равенства выражений – x ₁ + 3 и х ₁ + 2, соответствующих 2-й и 3-й чистым стратегиям второго игрока (см. табл. 31.5), поэтому y ₁ = y ₄ = 0, а у ₃ = 1 – y ₂.

Имеем

откуда

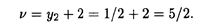
Оптимальное решение второго игрока (рис. 31.4):

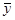_опт = (0,1 / 2,1 / 2,0), при этом цена игры v = 5/2.

Ответ.

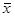_опт = (1/2, 1/2), 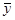_опт = (0,1 / 2,1 / 2,0), v = 5/2.

Пример 3. Найдем решение игры вида (т х 2), заданной пла­тежной матрицей (табл. 31.8)

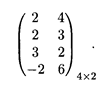
Решение. Находим α = mах (2, 2, 2, -2) = 2, β = min (3, 6) = 3, 2 ≤ v ≤ 3. Пусть y ₁ и у ₂ (причем y ₂ = l — y ₁) — смешанные стратегии второго игрока; x ₁, x ₂, x ₃, x ₄ — смешанные страте­гии первого игрока.

Находим

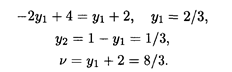
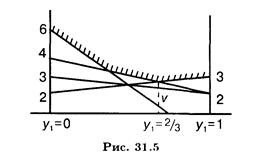
Оптимальное решение второго игрока (рис. 31.5):

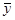_опт = (2/3, 1/3), при этом цена игры v = 8/3.

Прямые, пересекающиеся в минимаксной точке, соответ­ствуют 1-й и 3-й чистым стратегиям первого игрока. Это озна­чает, что х ₂ = х ₄ = 0. Следовательно, х ₁ = 1 — x ₃. Найдем оптимальную стратегию 1-го игрока (табл. 31.9, рис. 31.6).

Имеем

Оптимальное решение первого игрока:

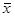_опт = (1/3, 0, 2/3, 0), при этом цена игры v = 8/3.

Ответ.

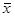_опт = (1/3, 0, 2/3, 0), 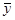_опт = (2/3, 1/3), v = 8/3.

31.2. Решение игр (a_ij)_{m x n} с помощью линейного программирования

Теория игр находится в тесной связи с линейным програм­мированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного про­граммирования и решена симплексным методом и, наоборот, задача линейного программирования может быть представле­на как игра.

Для первого игрока математическая модель задачи запи­сывается в виде

при ограничениях:

Математическую модель можно упростить, разделив все (п + 1) ограничений на v. Это возможно при v ≠ 0. При v = 0 рекомендуется прибавить любое положительное число ко всем элементам платежной матрицы, что гарантирует положи­тельность значения модифицированной игры. Действительное значение игры получается вычитанием из модифицированного значения этого положительного числа. Если v < 0, то надо сме­нить знаки неравенств. Полагая v > 0, систему ограничений можно записать так:

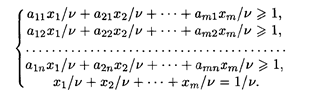
Положим Х_i = x_i/v. Так как v → max, то 1 / v → min. Получим задачу линейного программирования вида

при ограничениях:

Для второго игрока математическая модель записывается в виде

при ограничениях:

где S (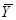) = 1 / v, Y_j = у_j / v.

Задача второго игрока является двойственной по отноше­нию к задаче первого игрока. Можно найти решение одного из игроков, а затем по теоремам двойственности — решение другого.

Дата добавления: 2014-10-15