Собственные значения и собственные векторы

End

6 2 -16

0 -6 -1

Вычисление корня квадратного из матрицы и матричной экспоненты

1 9 36

1 4 9

1 1 1

Поэлементное возведение в степень

0.0053 -0.0068 0.0018

Отрицательные и дробные степени

10 25 46

6 14 25

3 6 10

Положительные целые степени

Если А есть некоторая квадратная матрица, а р – положительное целое число, то A^p эквива-лентно умножению A на себя р раз.

X = A^2

X =

Если А является квадратной и невырожденной, то A^(-p) эквивалентно умножению inv(A) на себя p раз.

Y = B^(-3)

Y =

-0.0034 0.0001 0.0036

-0.0016 0.0070 -0.0051

Дробные степени, например A^(2/3), также допускаются; результаты при этом зависят от ра-спределения собственных значений матрицы А.

Оператор .^ (с точкой!) осуществляет поэлементное возведение в степень. Например,

X = A.^2

A =

Для невырожденных квадратных матриц А функция sqrtm вычисляет главное значение квад-ратного корня, т.е. если X = sqrtm(A), то X*X = A. Буква m в sqrtm означает, что выпол-няется матричная операция. Это отличает данную функцию от sqrt(A), которая, подобно A.^(1/2) (обратите внимание на точку!), выполняет операцию извленчения корня поэлемен-тно.

Система обыкновенных линейных дифференциальных уравнений первого порядка может быть записана в виде

dx/dt = Ax

где x = x(t) есть векторная функция от t, а A есть постоянная матрица не зависящая от t.

Решение данной системы может быть выражено в виде матричной экспоненты.

x(t) = ℮^Atx(0)

Функция expm(A) вычисляет матричную экспоненту. Рассмотрим пример системы диффере-нциальных уравнений со следующей 3х3 матрицей коэффициентов

A =

-5 20 -10

и начальными условиями x(0)

x0 = [ 1 1 1]’.

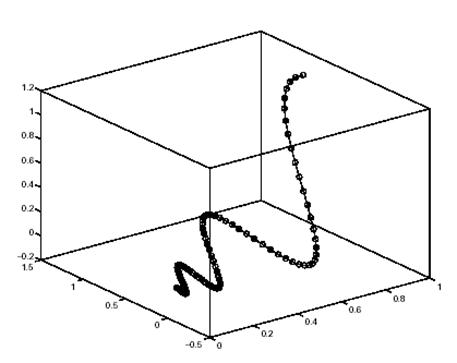
Использование матричной экспоненты для вычисления решения дифференциального уравне-ния в 101 точке с шагом 0.01 на интервале 0 ≤ t ≤ 1 записывается в виде

X = [ ];

for t = 0: 0.01: 1

X = [X expm(t*A)*x0];

Трехмерный график решения в фазовом пространстве может быть получен при помощи спе-циальной функции

plot3(X(1,:), X(2,:), X(3,:), '-o')

Решение имеет вид спиральной функции сходящейся к началу координат (см. рис. ниже). Та-кое решение обусловлено комплексными собственными значениями матрицы коэффициен-тов А.

Собственным значением и собственным вектором квадратной матрицы А называются ска-ляр λ и вектор v, удовлетворяющие условию

Av = λv

Дата добавления: 2014-10-15