Недоопределенные системы

0.3413

0.4760

1.0000 0.1003

1.0000 0.2019

1.0000 0.3329

1.0000 0.4493

1.0000 0.7408

1.0000 1.0000

2.3 0.50

1.6 0.55

1.1 0.60

0.8 0.63

0.3 0.72

0.0 0.82

T y

Переопределенные системы

6 0 -6

19 -3 -1

Квадратные системы

Наиболее часто встречающейся ситуацией является квадратная матрица коэффициентов A и одномерный вектор-столбец b справа, т.е. Ax = b. Решение x = A\b имеет при этом тот же ра-змер, что и вектор b. Например,

x = A\u

x =

-12

где матрица А есть приведенная выше матрица Паскаля. Легко удостовериться, что A*x в точности равно вектору u (численные значения этого вектора даны выше).

Если A и B являются квадратными и имеют одинаковый размер, то X = A\B имеет тот же ра-змер, например

X = A\B

X =

-17 4 13

Легко убедиться, что A*X в точности равно B.

Оба этих примера имеют точное решение в виде целых чисел. Это связано с тем, что в каче-стве матрицы коэффициентов была выбрана матрица Паскаля pascal(3), чей детерминант равен единице. Далее будут рассмотрены примеры влияния ошибок округления, возникаю-щих в более реальных системах.

Квадратная матрица A является сингулярной, если ее столбцы не являются линейно незави-симыми. Если A – сингулярна, то решение AX = B или не существует, или не является един-ственным. Оператор \, A\B, выдает предупреждающее сообщение, если матрица A близка к сингулярной и сообщение об ошибке, если определено равенство нулю детерминанта матри-цы А.

Переопределенные системы совместных линейных уравнений часто встречаются в задачах аппроксимации экспериментальных данных при помощи различных эмпирических кривых. Рассмотрим следующий гипотетический пример. Величина y измеряется при различных зна-чениях времени t, что дает следующие результаты

Эти данные могут быть введены в MATLAB при помощи выражений:

t = [0.3.8 1.1 1.6 2.3]';

y = [0.82 0.72 0.63 0.60 0.55 0.50]';

Данные могут быть аппроксимированы при помощи убывающей экспоненциальной функ-ции.

y(t) = c₁ + c₂ e^-t

Это уравнение показывает, что вектор y может быть представлен в виде линейной комбина-ции двух векторов, один из которых является постоянным вектором, содержащим все едини-цы, а второй вектор имеет компоненты e^-t. Неизвестные коэффициенты c₁ и c₂ могут быть найдены подгонкой кривых по методу наименьших квадратов,которая основана на миними-зации суммы квадратов отклонений экспериментальных данных от модели. Мы имеем шесть уравнений с двумя неизвестными, представленными 6х2 матрицей

E = [ones(size(t)) exp(-t)]

E =

Решение методом наименьших квадратов находится при помощи оператора \:

c = E\y

c =

Иными словами, подгонка методом наименьших квадратов дает

y(t) = 0.476 + 0.3413 e^-t

Следующие выражения оценивают модель при равномерно распределенных моментах време-ни (с шагом 0.1), а затем строят график вместе с результатами экспериментальных данных.

T = (0: 0.1: 2.5)';

Y = [ones(size(T)) exp(-T)]*c;

plot(T, Y, '-', t, y, 'o')

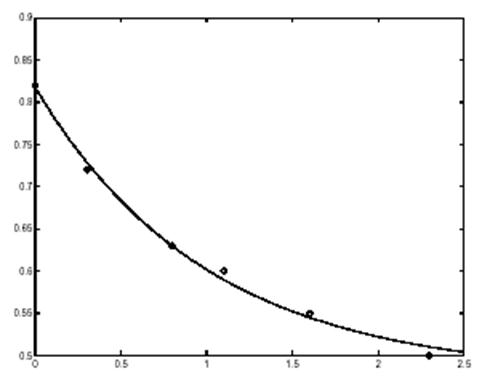
Можно видеть, что значения E*c не совсем точно совпадают со значениями эксперименталь-ных данных y, но эти отклонения могут быть сравнимы с ошибками измерений.

Прямоугольная матрица A называется матрицей неполного ранга, если ее столбцы линейно-независимы. Если матрица A имеет неполный ранг, то решение AX = B не является единст-венным. Оператор \ при этом выдает предупреждающее сообщение и определяет основное решение, которое дает минимально возможное число ненулевых решений.

Недоопределенные системы линейных уравнений содержат больше неизвестных чем урав-нений. Когда они сопровождаются дополнительными ограничениями, то становятся сферой изучения линейного программирования. Сам по себе, оператор \ работает только с системой без ограничений. При этом решение никогда не бывает единственным. MATLAB находит ос-новное решение, которое содержит по меньшей мере m ненулевых компонент (где m - число уравнений), но даже это решение может быть не единственным. Ниже приводится пример, где исходные данные генерируются случайным образом.

R = fix (10*rand(2,4))

R =

Дата добавления: 2014-10-15