Метод анализа иерархий

Наиболее распространенным является метод анализа иерархий (МАИ), который применяется для согласования результатов, полученных с использованием различных подходов и методов оценки [4].

МАИ, опирающийся на многокритериальное описание проблемы, был предложен и детально описан Т. Л. Саати в работе «Принятие решений: метод анализа иерархий». В методе используется дерево критериев, в котором общие критерии разделяются на критерии частного характера. Для каждой группы критериев определяются коэффициенты важности. Альтернативы также сравниваются между собой по отдельным критериям с целью определения критериальной ценности каждой из них. Средством определения коэффициентов важности критериев либо критериальной ценности альтернатив является попарное сравнение. Результат сравнения оценивается по балльной шкале. На основе таких сравнений вычисляются коэффициенты важности критериев, оценки альтернатив и находится общая оценка как взвешенная сумма оценок критериев.

Общая идея данного метода заключается в декомпозиции проблемы выбора на более простые составляющие части и обработку суждений лица, принимающего решение. В результате определяется относительная значимость исследуемых альтернатив по всем критериям, находящимся в иерархии.

Первым шагом МАИ является структурирование (декомпозиция) проблемы, согласование результатов в виде иерархии
(рис. 7.2). В наиболее простом виде иерархия строится с вершины, представляющей цель проблемы через промежуточные уровни, обычно являющиеся критерием сравнения к самому нижнему уровню, который в общем случае является набором альтернатив.

Верхний уровень - цель (например, определение рыночной стоимости); промежуточный уровень - критерии согласования (например, возможность отразить действительные намерения потенциального инвестора и продавца; тип, качество, обширность данных, на основе которых проводится анализ; способность параметров используемых методов учитывать конъюнктурные колебания; способность учитывать специфические особенности объекта, влияющие на его стоимость (местонахождение, размер, потенциальная доходность)); нижний уровень - набор альтернатив (например, результаты, полученные различными методами оценки).

	Альтернатива А1		Альтернатива …		Альтернатива А m

Рис. 7.2. Структура иерархии

На рис. 7.3 представлено дерево иерархий для принятия решения о величине рыночной стоимости объекта недвижимости на основе альтернативных результатов определения стоимости объекта тремя подходами: затратным, сравнительным и доходным. Дерево иерархий имеет двухуровневую систему анализируемых критериев. На первом уровне расположены основные факторы, определяющие достоверность результата оценки: исходная информация
и методология расчета. На втором уровне находятся критерии, характеризующие качество каждого из выделенных факторов.

Качество исходной информации в оценке определяется ее полнотой, достоверностью и соответствием требованиям рыночной стоимости. Именно эти критерии и указаны на дереве иерархий во втором уровне, под исходной информацией. Основными критериями качества для использованной методологии при расчетах стоимости являются:

- обоснованность выполнения предпосылок выбранного метода расчета в рамках каждого из подходов;

- субъективность применяемых допущений и предположений;

- учет принципа наиболее эффективного использования.

  Рыночная стоимость

Рис. 7.3. Дерево иерархий

Данные критерии качества указаны на дереве иерархий во втором уровне под методологией расчета.

Очень часто в практике оценки собственности используется следующий набор критериев:

- тип, качество, обширность данных, на основе которых проводится анализ;

- способность параметров используемых методов учитывать конъюнктурные колебания рынка;

- способность учитывать специфические особенности объекта, влияющие на его стоимость;

- возможность отразить действительные намерения продавца или покупателя.

Конечно же, можно указывать более развернутый перечень факторов, влияющих на достоверность определения рыночной стоимости, но это приведет к значительному повышению трудоемкости последующих вычислительных процедур.

После иерархического воспроизведения проблемы строится матрица сравнения критериев и рассчитывается значение приоритетов критериев.

Для этого попарно сравниваются критерии по отношению
к их воздействию на общую цель. Система парных сравнений приводит к результату, который может быть представлен в виде обратно симметричной матрицы, на главной диагонали которой находятся единицы.

Парные сравнения проводятся в терминах доминирования одной альтернативы над другой. Полученные суждения выражаются в целых числах с учетом девятибалльной шкалы. Преимущества именно этой шкалы качественных оценок отмечают многие исследователи, так как она позволяет наилучшим образом учесть степень отличия и имеет наименьшее среднеквадратическое отклонение.

Элементом матрицы a(i, j) является интенсивность проявления элемента иерархии i относительно элемента иерархии j, оцениваемая по шкале интенсивности от 1 до 9.

Заполняя матрицы парных сравнений, оценщик руководствуется следующими соображениями:

- если сравниваемые подходы по анализируемому критерию одинаково предпочтительны, то соответствующий элемент матрицы равен 1;

- если один из подходов имеет незначительное превосходство над другим по анализируемому критерию, то соответствующий элемент матрицы равен 3 или 4;

- если один из подходов имеет значительное превосходство над другим по анализируемому критерию, то соответствующий элемент матрицы равен 5 или 6;

- если один из подходов имеет явное превосходство над другим по анализируемому критерию, то соответствующий элемент матрицы равен 7 или 8;

- если один из подходов имеет абсолютное преимущество по сравнению с другим по анализируемому критерию, то соответствующий элемент матрицы равен 9.

Приведенное описание шкалы представлено в табл. 7.1.

Таблица 7.1

Шкала отношений интенсивности критериев оценки

Важность параметра оценки	1-9
Одинаковая важность
Незначительное преимущество
Значительное преимущество
Явное преимущество
Абсолютное преимущество
2, 4, 6, 8 – промежуточные значения

Таким образом, перед оценщиком ставится задача проанализировать при парном сравнении преимущества каждого из подходов по выделенным критериям второго уровня.

Процесс заполнения матриц парных сравнений, несмотря на кажущуюся тривиальность, является довольно трудоемкой процедурой. Но сложности на этом этапе заключаются не в громоздких расчетах, а в многообразии анализируемой информации. Например, при анализе полноты исходной информации, использованной в рамках каждого из подходов, оценщику необходимо ответить на вопрос: исходные данные какого из подходов были наиболее полными? Естественно, что понятие полноты для различных подходов определяется различными требованиями.

Полнота исходных данных для затратного подхода определяется наличием, например, следующей информации:

- объемно-планировочные и конструктивно-планировочные характеристики объекта оценки;

- данные о проводимых капитальных ремонтах;

- технические заключения об авариях на объекте;

- объемно-планировочные и конструктивно-планировочные характеристики объектов-аналогов.

Полнота исходных данных для сравнительного подхода определяется наличием, например, следующей информации:

- данные по основным ценоформирующим факторам объектов-аналогов;

- информация о предпочтениях потребителей на данном рынке объектов недвижимости.

Полнота исходных данных для доходного подхода определяется наличием, например, следующей информации:

- информация о состоянии рынка аренды для аналогичных объектов недвижимости;

- информация о предпочтениях потребителей на данном рынке объектов недвижимости.

Конечно, при заполнении матриц парных сравнений определенная доля субъективизма присутствует. Но объективность конечного результата определения весовых коэффициентов обеспечивается за счет полностью формализованных процедур, а именно расчета отношения согласованности суждений.

Пусть К₁…К _n - множество критериев из n элементов, тогда W ₁… W_n - интенсивности проявления этих элементов. Оценка весов критериев происходит по схеме, представленной в табл. 7.2.

При определении интенсивностей проявления критериев необходимо, чтобы соблюдались следующие обязательные условия:

W_{k -1}/ W_k + W_k / W_{k +1} > W_{k -1}/ W_k;

W_{k -1}/ W_k + W_k / W_{k +1} > W_k / W_{k +1},

где k Î [2; n ].

Таблица 7.2

Схема оценки весов критериев

Критерий	К1	К2	…	К n	Расчет	Вес критериев
К1		W 1/ W 2	...	W 1/ Wn		ВК1
К2	W 2/ W 1		…	W 2/ Wn		ВК2
…	…	…	…	…	…	…
К n	Wn / W 1	Wn / W 2	…			ВК n
Сумма

Информацию о степени отклонения от согласованности матрицы дает отношение согласованности.

Обычно в качестве допустимого используется значение отношения согласованности на уровне 10 %. Если для какой-либо матрицы парных сравнений это отношение превышает 0,1, то это свидетельствует о существенном нарушении логичности суждений, допущенном оценщиком при заполнении матрицы, поэтому оценщику предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить согласованность. Такая процедура предполагает заранее неизвестное число итераций пересмотра и изменения значений в матрицах парных сравнений с повторной проверкой на согласованность - до тех пор, пока не будет достигнут допустимый уровень согласованности оценок.

; (7.4)

, (7.5)

где ИС - индекс согласованности; λ_max - максимальное собственное число матрицы; S _{К i} - сумма интенсивностей проявления критериев по отношению к критерию К _i; В_{К i} - вес критерия К _i.

Для наших матриц всегда должно быть λ_max ≥ n.

Далее сравнивают эту величину индекса согласованности
с той, которая получилась бы при случайном выборе количественных суждений из нашей шкалы и образовании обратно симметричной матрицы.

Средние согласованности для случайных матриц разного порядка представлены в табл. 7.3.

Таблица 7.3

Средние согласованности для случайных матриц разного порядка

Размер матрицы
Случайная согласованность			0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49

Определяем отношение согласованности по формуле

, (7.6)

где ОС - отношение согласованности; СС - случайная согласованность матрицы n -го порядка.

Если разделить индекс согласованности на число, соответствующее случайной согласованности матрицы того же порядка, получим отношение согласованности.

Заключительным этапом в рассматриваемом методе является осуществление иерархического синтеза в целях определения вектора весовых коэффициентов альтернатив относительно выделенных критериев. Вычислительные процедуры данного этапа базируются на понятиях векторной алгебры.

Оценка весов альтернатив (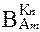) по каждому критерию производится аналогично оценке весов критериев.

Для определения итогового значения весов каждой альтернативы () синтезируются приоритеты начиная со 2-го уровня вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии с критериями, на которые воздействует элемент. Схема расчета представлена в табл. 7.4.

Таблица 7.4

Схема расчета итогового значения весов альтернатив

Критерии   Аль- тернативы	Вес альтернативы по каждому критерию	Итоговое значение веса для каждой альтернативы
К1	К2	…	К n
ВК1	ВК2	…	ВК n
А1			...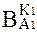
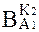
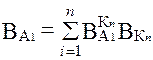
А2			...
…	…	…	…	…	…
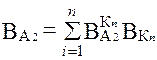
А m			...
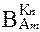
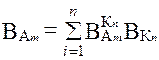
Сумма

Итоговый результат (рыночная стоимость) равен сумме произведений весов альтернатив () на соответствующие величины альтернатив ().

Рассмотрим использование предложенного метода на примере.

Приведем простой пример, поясняющий суть метода анализа иерархий.

Покупателю необходимо выбрать одну из трех квартир. Первоначально покупателю необходимо определить критерии, по которым он будет сравнивать квартиры. Возьмем для примера три критерия: местоположение, этаж, на котором расположена квартира, и состояние квартиры (цена всех трех квартир одинакова). В табл. 7.5 приведены характеристики квартир.

Таблица 7.5

Характеристики сравниваемых квартир

Альтернатива	Местоположение	Состояние	Этаж
Квартира 1	центр	плохое	первый
Квартира 2	периферия	среднее	четвертый
Квартира 3	окраина	отличное	второй

На втором этапе необходимо определить вес каждого критерия. Для этого попарно сравнивают все критерии:

- местоположение - состояние: местоположение имеет преимущество, но незначительное - 3;

- местоположение - этаж: местоположение имеет более значительное преимущество - 4;

- состояние - этаж: состояние имеет преимущество, но не очень значительное - 2;

- состояние - местоположение - 1/3;

- этаж - местоположение - 1/4;

- этаж - состояние - 1/2.

Для визуализации данной зависимости можно использовать следующую схему, представленную на рис. 7.4.

	Местоположение
	Состояние
Этаж

Рис. 7.4. Схема попарного сравнения критериев

Полученные значения подставляются в обратно симметричную матрицу, и рассчитываются веса критериев. Результаты расчета приведены в табл. 7.6.

На следующем этапе необходимо попарно сравнить каждую квартиру по каждому критерию.

Местоположение:

квартира 1 - квартира 2: квартира в центре имеет преимущество над квартирой на периферии - 4;

квартира 1 - квартира 3: квартира в центре имеет значительное преимущество над квартирой на окраине - 5;

квартира 2 - квартира 3: квартира на периферии более предпочтительна, чем квартира на окраине, но не значительно - 2;

квартира 2 - квартира 1 - 1/4;

квартира 3 - квартира 1 - 1/5;

квартира 3 - квартира 2 - 1/2.

Таблица 7.6

Расчет весов критериев

Критерий	Местоположение	Состояние	Этаж	Расчет	Вес
Местоположение
Состояние	1/3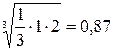
Этаж	1/4	1/2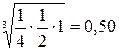
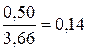
Сумма	3,66	1,00

Расчет представлен в табл. 7.7.

Таблица 7.7

Расчет весов квартир по критерию «местоположение»

Альтернатива	Квартира 1	Квартира 2	Квартира 3	Расчет	Вес
Квартира 1				2,71	0,68
Квартира 2	1/4			0,79	0,20
Квартира 3	1/5	1/2		0,46	0,12
Сумма	3,97	1,00

Аналогично сравнивают квартиры по другим критериям: состояние и этаж. Результаты расчета представлены в табл. 7.8 и 7.9.

Таблица 7.8

Расчет весов квартир по критерию «состояние»

Альтернатива	Квартира 1	Квартира 2	Квартира 3	Расчет	Вес
Квартира 1		1/4	1/7	0,33	0,07
Квартира 2			1/4	1,00	0,23
Квартира 3				3,04	0,70
Сумма	4,37	1,00

Таблица 7.9

Расчет весов квартир по критерию «этаж»

Альтернатива	Квартира 1	Квартира 2	Квартира 3	Расчет	Вес
Квартира 1		1/3	1/8	0,35	0,09
Квартира 2			1/2	1,14	0,28
Квартира 3				2,52	0,63
Сумма	4,01	1,00

Далее рассчитывается итоговый вес каждой квартиры. Результаты расчетов представлены в таблице 7.10.

Таблица 7.10

Расчет весов квартир

Критерий Аль-тернатива	Местоположение	Состояние	Этаж	Вес
0,62	0,24	0,14
Квартира 1	0,68	0,07	0,09	0,62×0,68+0,24×0,07+0,14×0,09=0,45
Квартира 2	0,20	0,23	0,28	0,62×0,20+0,24×0,23+0,14×0,28=0,22
Квартира 3	0,12	0,70	0,63	0,62×0,12+0,24×0,70+0,14×0,63=0,33
Сумма	1,00	1,00	1,00	1,00

Из результатов расчета видно, что квартира 1 предпочтительна для покупки (вес наибольший).

Далее приведен пример согласования результатов оценки по шести критериям:

А - полнота исходной информации;

Б - достоверность исходной информации;

В - соответствие исходной информации требованиям рыночной стоимости;

Г - учет принципа наиболее эффективного использования;

Д - обоснованность предпосылок выбранного метода расчета;

Е - количество и значимость субъективных показателей и предположений.

При проведении расчетов были получены следующие значения: по затратному подходу - 900 000 руб.; по рыночному - 1 000 000 руб.; по доходному 1 100 000 руб.

Расчет весов критериев представлен в табл. 7.11.

Таблица 7.11

Определение весов критериев

Критерий	А	Б	В	Г	Д	Е	Расчет	Вес критерия
А	1,00	0,33	3,00	0,25	1,00	2,00	0,89	0,1083
Б	3,00	1,00	5,00	0,50	3,00	4,00	2,12	0,2572
В	0,33	0,20	1,00	0,13	0,33	0,50	0,33	0,0406
Г	4,00	2,00	8,00	1,00	4,00	7,00	3,49	0,4235
Д	1,00	0,33	3,00	0,25	1,00	2,00	0,89	0,1083
Е	0,50	0,25	2,00	0,14	0,50	1,00	0,51	0,0621
Cумма	9,83	4,12	22,00	2,27	9,83	16,50		1,0000

;

;

λ_max = 9,83 · 0,89 + 4,12 · 2,12 + 22,00 · 0,33 + 2,27 · 3,49 + 9,83 · 0,89 +
+16,51 · 0,51= 6,066683;

;

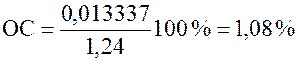< 10 %.

Определение весов подходов по каждому критерию представлено в табл. 7.12-7.17.

Таблица 7.12

Определение весов подходов по критерию А

Подходы к оценке	Затратный	Рыночный	Доходный	Расчет	Вес подхода по критерию А
Затратный	1,00	0,33	0,13	0,35	0,09
Рыночный	3,00	1,00	0,50	1,14	0,29
Доходный	8,00	2,00	1,00	2,52	0,63
Сумма	12,00	3,33	1,63	4,01	1,00

λ_max = 12,00 · 0,09 + 3,33 · 0,29 + 1,63 · 0,63 = 3,009202;

;

< 10 %.

Таблица 7.13

Определение весов подходов по критерию Б

Подходы к оценке	Затратный	Рыночный	Доходный	Расчет	Вес подхода по критерию Б
Затратный	1,00	6,00	3,00	2,62	0,67
Рыночный	0,17	1,00	0,50	0,44	0,11
Доходный	0,33	2,00	1,00	0,87	0,22
Сумма	1,50	9,00	4,50	3,93	1,00

λ_max = 3,000000; ИС = 0,000000; ОС = 0,00 % < 10 %.

Таблица 7.14

Определение весов подходов по критерию В

Подходы к оценке	Затратный	Рыночный	Доходный	Расчет	Вес подхода по критерию В
Затратный	1,00	0,20	3,00	0,84	0,19
Рыночный	5,00	1,00	7,00	3,27	0,73
Доходный	0,33	0,14	1,00	0,36	0,08
Сумма	6,33	1,34	11,00	4,48	1,00

λ_max = 3,064888; ИС = 0,032444; ОС = 5,59 % < 10 %.

Таблица 7.15

Определение весов подходов по критерию Г

Подходы к оценке	Затратный	Рыночный	Доходный	Расчет	Вес подхода по критерию Г
Затратный	1,00	0,50	3,00	1,14	0,30
Рыночный	2,00	1,00	6,00	2,29	0,60
Доходный	0,33	0,17	1,00	0,38	0,10
Сумма	3,33	1,67	10,00	3,82	1,00

λ_max = 3,000000; ИС = 0,000000; ОС = 0,00 % < 10 %.

Таблица 7.16

Определение весов подходов по критерию Д

Подходы к оценке	Затратный	Рыночный	Доходный	Расчет	Вес подхода по критерию Д
Затратный	1,00	7,00	3,00	2,76	0,68
Рыночный	0,14	1,00	0,50	0,41	0,10
Доходный	0,33	2,00	1,00	0,87	0,22
Сумма	1,48	10,00	4,50	4,05	1,00

λ_max = 3,002641; ИС = 0,001320; ОС = 0,23 % < 10 %.

Таблица 7.17

Определение весов подходов по критерию Д

Подходы к оценке	Затратный	Рыночный	Доходный	Расчет	Вес подхода по критерию Е
Затратный	1,00	4,00	5,00	2,71	0,68
Рыночный	0,25	1,00	2,00	0,79	0,20
Доходный	0,20	0,50	1,00	0,46	0,12
Сумма	1,45	5,50	8,00	3,97	1,00

λ_max = 3,024595; ИС = 0,012297; ОС = 2,12 % < 10 %.

Итоговый расчет рыночной стоимости, согласованной методом анализа иерархий, представлен в табл. 7.18.

Таблица 7.18

Итоговое определение рыночной стоимости

Показатели	А	Б	В	Г	Д	Е	Итоговый вес подхода	Расчеты по подходам	Взвешенный результат
Вес критерия	0,1083	0,2572	0,0406	0,4235	0,1083	0,0621
Затрат-ный	0,09	0,67	0,19	0,30	0,68	0,68	0,4318	900 000	388 625
Рыноч-ный	0,29	0,11	0,73	0,60	0,10	0,20	0,3668	1000 000	366 755
Доход-ный	0,63	0,22	0,08	0,10	0,22	0,12	0,2014	1100 000	221 583
Сумма	1,00		976 963

0,4318 = 0,1083×0,09 + 0,2572×0,67 + 0,0406×0,19 + 0,4235×0,30 +
+ 0,1083×0,68 + 0,0621×0,68;

388 625 = 900 000×0,4318.

По результатам согласования результатов оценки методом анализа иерархий рыночная стоимость составляет 976 963 руб. или округленно 977 000 руб.

Подводя итоги сказанного, можно отметить, что избежать субъективизма при согласовании результатов в течение всего процесса оценки просто невозможно. Можно лишь с помощью каких-то методов, приемов, процедур попытаться уменьшить степень субъективизма, в том числе и при согласовании результатов.

Дата добавления: 2014-10-31