Векторная диаграмма

Всякая синусоидальная величина может быть представлена вектором, вращающимся с постоянной угловой скоростью.

Пусть имеется радиус-вектор Е_м, равномерно вращающийся в направлении стрелки (рис.6, а).

Предположим, что его начальное положение совпадает с положительным направлением оси хх. Тогда проекция радиуса-вектора на ось уу будет изменяться в зависимости от угла поворота α по закону синуса (например, для угла α ₁ проекция вектора Е_м будет е ₁ = Е_м sin α ₁).

Откладывая по оси абсцисс угол поворота радиуса-вектора, а по оси ординат – его проекция на ось уу, можно получить синусоидальную кривую е = Е_м sin α (рис.6, б).

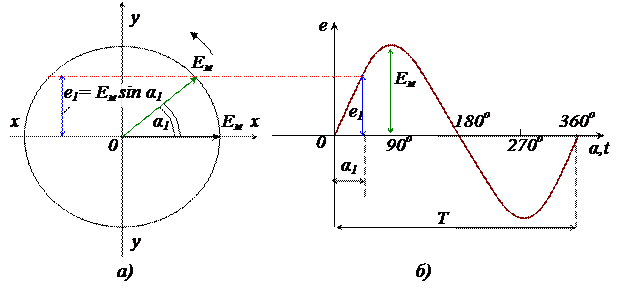
а – векторная; б – волновая.

Рисунок 6 – Диаграммы э.д.с.

Одному полному обороту вектора будет соответствовать один цикл изменений синусоидальной величины, или один период.

Отсюда вытекает, что синусоидальную функцию можно представить не волновой кривой, а вращающимся вектором. Тогда длина вектора в некотором масштабе будет равна амплитуде синусоидальной величины, а его проекция на вертикальную ось – мгновенному значению. Скорость вращения вектора будет характеризовать число периодов в секунду, или частоту.

Угол 2π описывается вектором за время Т, поэтому угловая скорость вращения вектора (или угловая частота) будет равна

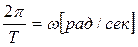. (6)

Так как 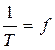есть частота, то 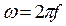. При промышленной частоте f = 50 Гц ω = 314 рад/сек.

Угол α, описанный вектором за время t, будет равен

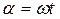. (7)

Этот угол, характеризующий отдельные стадии синусоидального процесса, носит название фазового угла или фазы. Необходимо иметь в виду, что углу α на векторной диаграмме (рис.6, а) будет соответствовать тот же угол на волновой диаграмме (рис.6, б).

Угол φ, соответствующий началу отсчета времени (t = 0), называется начальным фазовым углом или начальной фазой (рис.7, а и б).

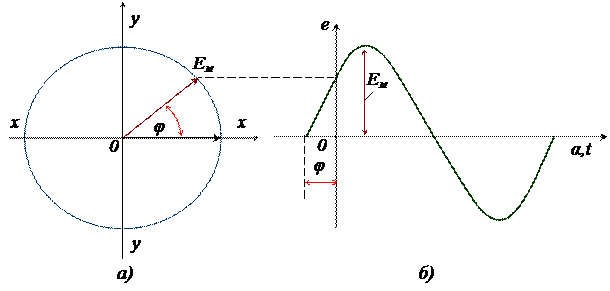
а – векторная; б – волновая.

Рисунок 7 – Диаграммы э.д.с. с начальной фазой φ.

Условимся считать угол φ положительным, если он получается поворотом вектора из начального положения против вращения часовой стрелки.

Разность начальных фаз двух синусоидальных величин одного периода называется углом сдвига фаз и обозначается буквой φ.

На рисунке 8, б и в показаны две синусоидальные функции одного периода с различными начальными фазами. Векторная кривая с начальной фазой, равной нулю (рис.8, в), выражается уравнением

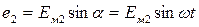. (8)

Первая кривая с начальной фазой, равной 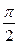, выражается уравнением

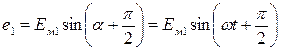. (9)

Угол сдвига фаз между кривыми равен 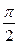. В этом случае максимальные значения кривых не совпадают во времени.

Две сдвинутые на угол 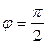э.д.с. практически можно получить, если два витка (1 и 2), совмещенные в пространстве друг относительно друга на угол 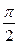, одновременно вращать в магнитном поле (рис.8, а). Положение витков

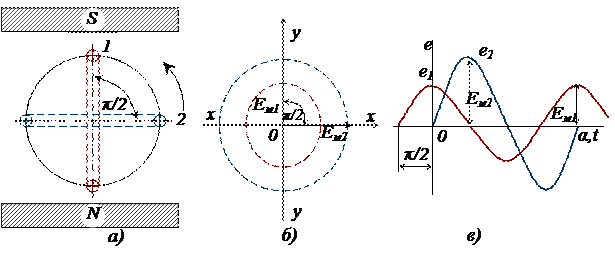
а – получение сдвига фаз на угол 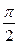; б – векторная диаграмма; в – волновые диаграммы

Рисунок 8 – Получение э.д.с., имеющих сдвиг фаз на угол .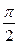

соответствует начальному моменту времени (t = 0), когда э.д.с. в витке 2 равна нулю, а в витке 1 – максимуму. При вращении обоих витков в однородном магнитном поле э.д.с. в каждом витке будет изменяться по синусоидальному закону. Однако значения э.д.с. в витке 1 будут опережать на четверть периода (или на угол 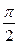по фазе) значения э.д.с. в витке 2, что и показано на волновой (рис.8, в) и векторной (рис.8, б) диаграммах (вектор Е_{м 1} опережает по фазе на угол 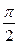вектор Е_{м 2}).

Законы Ома и Кирхгофа для цепей постоянного тока будут справедливы в алгебраической форме для мгновенных значений величин в цепях переменного тока.

При изучении переменных токов приходится часто суммировать или вычитать однородные электрические величины. Пусть, например, в цепи имеются две переменные э.д.с. с одинаковыми периодами. Мгновенные значения их равны:

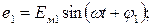(10)

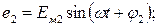(11)

Мгновенное значение суммарной э.д.с. будет равно алгебраической сумме мгновенных значений слагаемых величин

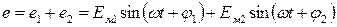. (12)

Мгновенное значение э.д.с. е ₁ и е ₂ представляют проекции векторов 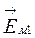и 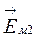на вертикальную ось (рис.8). следовательно, 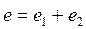есть сумма проекций векторов 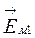и 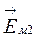. Как известно из механики, сумма проекций векторов равна проекции их геометрической суммы. Поэтому, чтобы найти величину е, необходимо геометрически сложить векторы 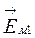и 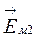и результирующий вектор спроектировать на вертикальную ось. Тогда 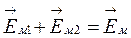будет представлять собой амплитуду синусоидальной величины

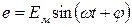. (13)

Отсюда можно сделать вывод, что алгебраическому сложению синусоидальных функций с одинаковыми периодами будет соответствовать геометрическое сложение амплитуд этих функций. Следовательно, вместо того чтобы алгебраически складывать ординаты синусоид, можно геометрически сложить векторы (т.е. амплитуды) этих синусоид. Геометрическая сумма этих векторов и будет представлять амплитуду результирующей синусоидальной величины.

При изучении явлений в цепях переменного тока представляет особый интерес относительное расположение векторов на векторной диаграмме. При одинаковой частоте оно остается постоянным. Поэтому при операциях с векторами последние условно можно считать неподвижными.

Лекция №4

Дата добавления: 2014-10-31