Цепь переменного тока с индуктивностью

Пусть имеется электрическая цепь переменного тока с потребителем, содержащим только одну индуктивность L (рис. 11).

Активное сопротивление цепи R и емкость C будем считать равными нулю, а L = const. Это будет идеальная цепь, так как любой потребитель имеет также активное сопротивление и емкость.

Практически потребителем с чистой индуктивностью может быть катушка, состоящая из большого числа витков проволоки с большим поперечным сечением и малым удельным сопротивлением. Если бы такая катушка была включена в цепь постоянного тока, то ток в ней был бы весьма большим, так как при R ≈ 0 имелось бы фактически короткое замыкание. При включении индуктивной катушки в цепь переменного тока такого явления не наблюдается, так как ток в ней при значительном числе витков обычно не достигает больших значений. Указанное обстоятельство объясняется тем, что при изменении тока в цепи по величине и направлению изменяется создаваемый током магнитный поток, пронизывающий катушку (сцепленный с проводниками катушки). Циклически изменяющийся магнитный поток вызывает появление в катушке э.д.с. самоиндукции, которая во время возрастания тока направлена против него, а при убывании тока имеет одинаковое с ним направление. Таким образом, э.д.с. самоиндукции в соответствии с законом Ленца препятствует как увеличению, так и уменьшению тока. Как будет показано далее, результирующее действие э.д.с. самоиндукции, препятствующей всем изменениям тока, в конечном итоге ограничивает величину амплитуды, а следовательно, и действующее значение тока. Таким образом, индуктивность в цепи оказывает дополнительное препятствие (сопротивление) для прохождения переменного тока, называемое индуктивным сопротивлением.

Индуктивность в цепях постоянного тока может проявляться только в нестационарных режимах (т.е. при включении, отключении и всяких изменениях тока по величине).

К индуктивным сопротивлениям относят катушки со стальным сердечником (и без него), имеющие большое число витков проволоки. При этом иногда полностью пренебрегают их активным сопротивлением. Индуктивными сопротивлениями обладают такие части аппаратов, приборов и машин, в которых при прохождении тока создаются большие магнитные потоки (например, обмотки электродвигателей, генераторов, трансформаторов, катушки контакторов и реле и т.д.).

Предположим, что в цепи, показанной на рис. 11, ток, обусловленный синусоидальным напряжением генератора, изменяется по синусоидальному закону, т.е.

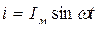. (21)

Рисунок 11 – Цепь с индуктивным сопротивлением.

Изменения тока в цепи вызовут появления э.д.с. самоиндукции

. (22)

Подставляя значение i в формулу (22), получим

(23)

Из выражения (23) следует, что э.д.с. самоиндукции е_L будет отставать по фазе от тока i на угол (или на периода).

Наибольшее значение е_L,будет при

Следовательно,

. (24)

Разделив обе части равенства (24) на 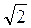, получим

.

На рис. 12 показаны волновая и векторная диаграммы э.д.с. и тока.

Рисунок 12 – Векторная и волновые диаграммы цепи с индуктивным сопротивлением

Для рассматриваемой цепи составим уравнение по второму закону Кирхгофа

.

так как

.

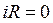Отсюда

, (25)

т.е. в любой момент времени мгновенное значение приложенного к цепи напряжения равно и противоположно по знаку э.д.с. самоиндукции. Следовательно, все ординаты кривой напряжения (в том числе и амплитуды) будут равны и противоположны по знаку ординатам кривой э.д.с. самоиндукции. Поэтому кривая и (см. рис. 12) будет сдвинута относительно кривой е_L на угол 180^о (или π). На такой же угол будут сдвинуты и векторы этих величин.

Так как , то выражение (23) для и можно представить в следующем виде

, (26)

что вытекает из сравнения построенных кривых на рис 12.

Амплитуда напряжения будет равна

, (27)

откуда амплитуда тока

. (28)

Разделив обе части выражения (28) на 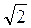, получим

. (29)

Выражения (28) и (29) представляют закон Ома для амплитудных и действующих значений в цепях переменного тока, содержащих только индуктивность.

Величина называется индуктивным сопротивлением, или реактивным сопротивлением индуктивности, и измеряется в Омах.

В самом деле, размерность х_L будет

.

Мгновенная мощность в цепи переменного тока с индуктивностью будет равна

(30)

Из выражения (30) следует, что мгновенная мощность изменяется по синусоидальному закону с двойной частотой по отношению к частоте переменного тока.

Кривую мгновенной мощности можно получить также путем умножения ординат тока и напряжения (рис.12).

В течение первой и третьей четвертей периода, при возрастании тока от нуля до максимального значения, мощность положительна. Это значит, что генератор посылает энергию в индуктивную катушку, где она накапливает в виде энергии магнитного поля; при этом э.д.с. самоиндукции направлена против тока.

В течение второй и четвертой четвертей периода, при убывании тока от максимального значения до нуля, мощность отрицательна. Это значит, что энергия, накопленная в магнитном поле катушки, при уменьшении поля возвращается обратно генератору; при этом э.д.с. самоиндукции совпадает по направлению с током.

Таким образом, происходит периодический обмен энергией между генератором и катушкой с индуктивностью. Э.д.с. самоиндукции как бы играет роль промежуточного звена в этом обмене.

Средняя мощность, развиваемая генератором в течение периода, будет равна

. (31)

Следовательно, и энергия, отдаваемая генератором в сеть за период, будет также равна нулю. Поэтому в цепи с индуктивностью отсутствует необратимый процесс преобразования электрической энергии в тепловую или механическую.

Энергия, полученная катушкой от генератора за четверть периода:

, (32)

т.е. она равна энергии, запасенной в магнитном поле катушки.

Мощность в цепи, содержащей только индуктивное сопротивление, оценивается по ее наибольшему значению (т.е. по амплитуде) и называется реактивной мощностью. Как было уже сказано, реактивная мощность идет на образование магнитного поля потребителя, а затем возвращается генератору.

Как видно из рис. 12, максимальное значение реактивной мощности наступит при (или при ).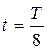

Амплитуда мощности, или реактивная мощность, будет равна

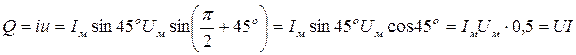(33)

Реактивная мощность измеряется в вольт-амперах или киловольт-амперах реактивных (вар или квар).

Обобщая изложенное, можно сделать следующие выводы:

- в цепях переменного тока только с индуктивным сопротивлением (R = 0; С = 0) ток отстает по фазе от приложенного напряжения на угол 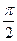, или на четверть периода во времени.

- закон Ома справедлив для амплитудных и действительных значений тока и напряжения. Сопротивлением в данном случае является величина , выражаемая в Омах и называемая индуктивным сопротивлением или реактивным сопротивлением индуктивности. Это сопротивление – следствие реакции магнитного поля при изменениях тока в цепи.

- при прохождении тока в цепи происходят периодические колебания энергии от генератора к катушке и от катушки к генератору. Роли генератора и потребителя периодически взаимно меняются. Так как R = 0, то средняя мощность и энергия за период равны нулю.

Лекция № 6.

Дата добавления: 2014-10-31