Параллельный сумматор с одновременным переносом

Параллельный сумматор со сквозным переносом

При построении сумматора со сквозным переносом представим выражение для сигнала переноса в следующем виде:

P_i+1=a_ib_iÈa_iP_iÈb_iP_i=a_ib_iÈ(a_iÈb_i)P_i=C_iÈT_iP_i,

где C_i=a_ib_i – собственный перенос, сформированный в i -ом разряде;

T_i=a_iÈb_i - признак распространения переноса, образованного в предыдущих разрядах, через i -разряд;

T_i×P_i - транзитный перенос, т.е. перенос из предыдущих разрядов, проходящий через i -й разряд.

С учетом полученного выражения для P_i+1 схема сумматора со сквозным переносом может быть представлена в виде.

В этой схеме предполагается, что в каждом i -ом одноразрядном комбинационном сумматоре формируется кроме S_i еще и C_i=a_ib_i и T_i=a_iÈb_i.

Время суммирования m разрядных чисел равно t_å= t_зå+(m-1)t_зр,

где t_зå – время задержки в одноразрядном сумматоре сигнала на выходе S (суммы), t_зр - задержка в цепях формирования переноса. Отличительная особенность таких сумматоров заключается в том, что формирование переноса производится до образования цифры суммы в каждом разряде, что и способствует увеличению быстродействия.

Время формирования суммы может быть еще уменьшено, если использовать сумматоры с одновременным (параллельным) переносом. Принцип построения таких сумматоров заключается в том, что значение каждого разряда суммы получается в результате одновременного анализа данного и всех более младших разрядов слагаемых. Для вывода формулы одновременного переноса в (i+1) -ый разряд (P_i+1) представим все формулы сквозного переноса для каждого разряда:

P₁

P₂=C₁ÈT₁P₁

P₃=C₂ÈT₂P₂

.....

P_i=C_i-1ÈT_i-1P_i-1

P_i+1=C_iÈT_iP_i

Подставив в уравнение P_i+1 значение P_i, получим

P_i+1=C_iÈT_iС_i-1ÈT_iT_i-1P_i-1.

Подставляя в это уравнение P_i-1 имеем

P_i+1=C_iÈT_iС_i-1ÈT_iT_i-1C_i-2ÈT_iT_i-1T_i-2P_i-2 и т.д.

В конечном счете логическое уравнение переноса в (i+1) разряд, выраженное через значения разрядов слагаемых имеет вид:

P_i+1=C_iÈT_iС_i-1ÈT_iT_i-1C_i-2ÈT_iT_i-1T_i-2C_i-3È…ÈT_iT_i-1T_i-2…T₃T₂C₁ÈT_iT_i-1T_i-2…T₃T₂T₁P₁

Из этого уравнения следует, что на выходе i -го разряда перенос P_i+1 возникает тогда, когда он образован в данном разряде, или если он был образован в некотором предыдущем разряде, а во всех последующих разрядах, включая данный, выполняется условие распространения переноса. Следовательно, перенос в каждом разряде может быть выработан одновременно с запуском переноса P₁ в младший разряд. Из этого уравнения может быть образована система уравнений для сумматора с одновременным переносом. Система уравнений для четырехразрядного сумматора имеет следующий вид:

P₁

P₂=C₁ÈT₁P₁

P₃=C₂ÈT₂C₁ÈT₂T₁P₁

P₄=C₃ÈT₃C₂ÈT₃T₂C₁ÈT₃T₂T₁P₁

На основании записанной системы уравнений строится схема сумматора с одновременным переносом, которая имеет следующий вид.

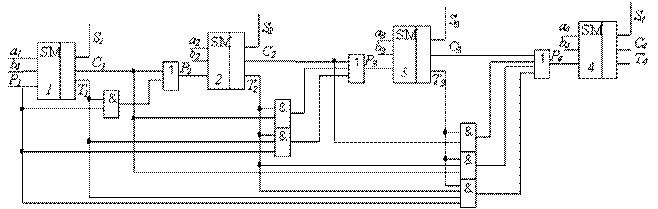
Т.к. слагаемые А и В в такой схеме подаются параллельно, то и переносы формируются одновременно. Время суммирования чисел в таком сумматоре равно t_å= t_зå+t_зр,

t_зå - время задержки формирования сигнала суммы (S_i), t_зр - время задержки формирования сигнала переноса. Схема формирования сигнала переноса на элементах булевого базиса в каждом разряде трехуровневая (один уровень – вычисление T_i и С_i, второй и третий уровни получение P_i+1 по сформированным - T_i и С_i). Поэтому t_зр=3Dt, где Dt – задержка сигнала в одном логическом элементе. Такие сумматоры являются самыми быстродействующими.

Из приведенной схемы видно, что цепи формирования сигнала переноса с увеличением номера разряда i усложняются и сам сумматор, в отличие от ранее рассмотренных, построен на неоднотипных схемах разрядов, т.е. является не регулярным. (Регулярными являются сумматоры, построенные на однотипных схемах, например сумматоры с последовательным и сквозным переносами). Поэтому существующие ограничения по нагрузочной способности и коэффициенту объединения не позволяют строить сумматоры с одновременным переносом на большее число разрядов. На практике используют в зависимости от требуемого быстродействия различные схемы сумматоров с групповым переносом.

Дата добавления: 2014-10-31