Ти разрядный сумматор с одновременным переносом между группами

Параллельные сумматоры с групповым переносом

В сумматорах с групповым переносом все разряды разбиваются на группы по P разрядов (обычно P=4¸6), причем в пределах каждой из групп перенос организуется по одновременному или сквозному методу. Между группами перенос может быть либо одновременным, либо сквозным. Например, 12-ти разрядный сумматор с одновременным переносом между группами (в каждой группе 4 разряда) имеет вид.

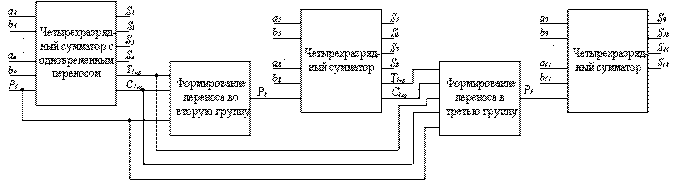
Здесь каждый четырех разрядный сумматор с одновременным переносом строится также - как это было рассмотрено ранее.

C_jгр - сигнал переноса из j группы (собственный перенос). Этот перенос вычисляется по формуле:

P_i+1=C_iÈT_iС_i-1ÈT_iT_i-1C_i-2ÈT_iT_i-1T_i-2C_i-3È…ÈT_iT_i-1T_i-2…T₃T₂C₁ÈT_iT_i-1T_i-2…T₃T₂T₁P₁, .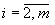

T_jгр - сигнал условия прохождения через j -ую группу (признак транзитного переноса).

T_jгр =T_lT_l-1…T_k, где k – номер младшего разряда в группе, l - номер старшего разряда в группе.

T_i – признак прохождения переноса через i -ый разряд.

Для нашей схемы:

P₂=C_1грÈT_1гр×P₁

P₃=C_2грÈT_2гр×P₂=С_2грÈT_2грС_1грÈT_2грT_1грP₁

В свою очередь:

T_1гр=T₁T₂T₃T₄; T_2гр=T₅T₆T₇T₈, где T_i=a_iÈb_i.

C_1гр=C₄ÈT₄С₃ÈT₄T₃C₂ÈT₄T₃T₂C₁È T₄T₃T₂T₁P₁

C_i=a_i×b_i – перенос из i -го разряда (собственный).

C_2гр=C₈ÈT₈С₇ÈT₈T₇C₆ÈT₈T₇T₆C₅È T₈T₇T₆T₅P₂

Очевидно, такой сумматор будет иметь меньшую сложность, чем аналогичный сумматор с одновременным переносом от всех 12-ти разрядов, но будет и менее быстродействующим, т.к. добавляются цепи для формирования С _jгр и T_jгр, в которых будет дополнительная задержка сигнала.

Раздел 5. Лекция 13. Абстрактный синтез конечных автоматов

При синтезе комбинационных схем можно составить таблицу зависимости значения выходного сигнала от комбинации входных. Такая таблица однозначно определяет систему переключательных функций, описывающую работу комбинационной схемы. Составить аналогичную таблицу, описывающую работу конечного автомата (КА), не представляется возможным, так как множество допустимых входных слов автомата, вообще говоря, бесконечно. Поэтому для задания КА и используются таблицы переходов и выходов, которые позволяют представить соответствие между бесконечными множествами входных и выходных слов конечными таблицами. В связи с этим, прежде чем приступить к синтезу схемы КА, необходимо составить таблицу переходов и выходов, что не всегда является простым делом особенно в тех случаях, когда алгоритм работы автоматов задан в описательной форме. Для того чтобы упростить и формализовать процедуру построения таблиц переходов и выходов, необходимо ввести такую исходную форму задания автоматов, переход к которой от алгоритмов, сформулированных в описательной форме, не представляет трудностей. Мы рассмотрим один из возможных способов формального задания автоматов, а именно, задание автомата на языке регулярных событий.

Дата добавления: 2014-10-31