Представление событий в автоматах

В основе рассматриваемого способа задания автоматов, лежит понятие событий, представимых в автоматах.

Пусть Y { y ₁, y ₂, …, y _k} – выходной алфавит конечного автомата S с фиксированным начальным состоянием a ₀. Тогда каждой букве y _j, выходного алфавита можно поставить в соответствие множество входных слов S _j(x ₁, x ₂,…, x _m), которые вызывают появление на выходе автомата буквы y_j. Определенное таким образом множество слов S _j(x ₁, x ₂, …, x _m) называют событием, представленным в автомате выходным сигналом y _j.

Поэтому для задания конечного автомата, имеющего выходной алфавит Y { y ₁, y ₂, …, y _k}, достаточно разбить множество всех возможных входных слов на K событий S ₁, S ₂, …, S _k, представленных в автомате выходными сигналами y ₁, y ₂, …, y _k соответственно. Для частичного автомата необходимо, кроме того, задать множество S _з запрещенных слов. Таким образом, конечный автомат может быть задан таблицей, устанавливающей соответствия между событиями и буквами выходного алфавита. Зная набор событий S _j, можно, не пользуясь таблицами переходов и выходов, найти реакцию автомата на любое входное слово, для чего достаточно определить множество каких слов входного алфавита оно входит (то есть какому событию принадлежит).

Для описания автоматов на языке регулярных событий вводят ряд операций над событиями, то есть строят алгебру событий. Мы рассмотрим алгебру событий, введенную Клини и усовершенствованную академиком Глушковым В. М.

Соответствие событий буквам выходного алфавита

Событие	Буква
S1(x1, x2,…, xm) S2(x1, x2,…, xm) … Sk(x1, x2,…, xm) Sз(x1, x2,…, xm)	y1 y2 … yk -

Операции в алгебре событий. Алгебра событий включает три операции: дизъюнкцию (объединение) событий, произведение событий и итерацию событий.

Дизъюнкцией событий называют событие S = S ₁v S ₂v…v S _k, состоящее из всех слов, входящих в события S ₁, S ₂, …, S _k.

Пример:
Событие S ₁ содержит слова x ₁, x ₂ x ₁, x ₁ x ₁, т.е. S ₁ = (x ₁, x ₂ x ₁, x ₁ x ₁), а
S ₂=(x ₂, x ₁ x ₂). Тогда S = S ₁ v S ₂ = (x ₁, x ₂, x ₁ x ₁, x ₁ x ₂ x ₂ x ₁).

Произведением событий называется событие S = S ₁* S ₂* …,* S _k, состоящее из всех слов, полученных приписыванием к каждому слову события S 1 каждого слова события S ₂, затем слова события S ₃ и т.д.

Пример:
S ₁ и S ₂ те же. Тогда S = S ₁* S ₂ = (x ₁ x ₂, x ₁ x ₁ x ₂, x ₂ x ₁ x ₂, x ₂ x ₁ x ₁ x ₂, x ₁ x ₁ x ₂, x ₁ x ₁ x ₁ x ₂). Произведение событий не коммутативно, то есть слова, входящие в события S ₁* S ₂ и S ₂ *S ₁ различны: то есть S ₁ *S ₂ 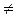S ₂ *S ₁. Поскольку произведение не коммутативно, следует различать операции «умножение справа» и «умножение слева». Например, относительно произведения событий S ₁ *S ₂ можно сказать, что событие S ₂ умножено на событие S ₁ справа, а событие S ₁ на S ₂ – слева.

Третьей операцией, применяемой в алгебре событий, является одноместная операция итерация, которая применима только к одному событию. Для обозначения итерации вводят фигурные скобки, которые называются итерационными.

Итерацией события S называется событие{ S }, состоящее из пустого слова e и всех слов вида S, SS, SSS и т.д. до бесконечности. То есть:
{ S } = e v S v SS v SSS v …

Пример:
S =(x ₂, x ₁ x ₂), { S } = (e, x ₂, x ₂ x ₂, x ₂ x ₂ x ₂, …, x ₁ x ₂, x ₁ x ₂ x ₁ x ₂, …, x ₂ x ₁ x ₂, x ₁ x ₂ x ₂, …)

При синтезе конечных автоматов важнейшую роль играют регулярные события. Очевидно любое событие, состоящее из конечного множества слов, является регулярным. Действительно, такие события можно представить в виде дизъюнкции всех входящих в него слов, образованных из букв заданного алфавита с помощью операции умножения. События, состоящие из бесконечного числа слов, могут быть как регулярными, так и не регулярными.

Теорема: Любые регулярные выражения и только они представимы в конечных автоматах.

Из этой теоремы следует, что любой алгоритм преобразования информации, который можно записать в виде регулярного выражения, реализуется конечным автоматом. С другой стороны, любые конечные автоматы реализуют только те алгоритмы, которые могут быть записаны в виде регулярных выражений.

Рассмотрим, как можно совершить переход от описательной формы задания алгоритмов работы конечных автоматов к представлению этих алгоритмов в виде регулярных выражений. С целью упрощения такого перехода вводят основные события, из которых с помощью операций дизъюнкции, умножения и итерации можно составить более сложные события, соответствующие заданному алгоритму работы автомата. За основные события принимают такие события, которые более часто встречаются в инженерной практике при синтезе схем ЭВМ.
Пусть дан конечный алфавит X = (x ₁, x ₂, …, x _m).

Регулярное событие – это любое событие, которое можно получить из букв данного алфавита с помощью конечного числа операций дизъюнкции, произведения и итерации. Регулярное выражение – любое выражение, составленное с помощью операций дизъюнкции, произведения и итерации.

Дата добавления: 2014-10-31