Второй пример абстрактного синтеза

Рассмотрим еще один пример абстрактного синтеза автомата. Найдем таблицу переходов автомата сравнения чисел, условия работы которого заданы регулярными выражениями:

Регулярные выражения

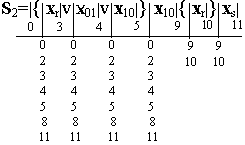
Регулярные выражения событий S ₁ и S ₂ содержат одинаковые сомножители в итерационных скобках, перед которыми расположено место с индексом 0. Поэтому в обоих выражениях основные места внутри итерационных скобок отмечены одинаковыми индексами (3, 4 и 5). Индекс конечного места каждого выражения распространяется на начальные места всех регулярных выражений, так как в автоматах многократного действия за словом любого события, например S ₁, может быть подано слово любого другого события, то есть S ₁ v S ₂ v S ₃. В размеченных выражениях можно объединить места с индексами 4, 6 и 5, 9:

По размеченному выражению составим отмеченную таблицу переходов.

yg

е

е

y3

е

е

е

е

y1

е

y2

е

е

е

е

xj\ai

1v3

3v6

3v8

*

xr

1v3

1v3

3v6

3v8

1v3

1v3

1v3

3v6

3v8

*

x01

*

*

*

*

x10

*

*

*

*

xs

*

*

При составлении таблицы следует учитывать, что для разных регулярных выражений автомат под действием одних и тех же входных сигналов переходит в разные состояния. Эти внутренние состояния будем отмечать множеством индексов основных мест. Например. В событии S ₃ переход из состояния 0 в состояние 1 происходит под действием сигнала x _r а в S ₁ под действием этого же сигнала из состояния 0 автомат переходит в состояние 3. Поэтому, внутреннее состояние, в которое автомат переходит под действием x_r из состояния 0, будем обозначать множеством из двух индексов 1 v 3. Аналогично получается переход из состояний 2, 7 и 9 под действием x _r, а также переход из состояния 4 и 5 в состояния 3 v 6 и 3 v 8 соответственно под действием x _r. При заполнении таблицы получается свободные клетки там, где переходы в автомате не определенны. Такие клетки будем отмечать звездочкой *, которую следует рассматривать как индекс некоторого внутреннего состояния. Таблица переходов составляется не только для состояний, отмеченных индексами основных мест регулярного выражения, но и для состояний, отмеченных множеством индексов. Для заполнения колонок для таких состояний достаточно образовать дизъюнкцию таких индексов, которые расположены в колонках, отмеченных индексами, входящими в множества. Например. Для заполнения колонки 1 v 3 образуем дизъюнкцию индексов расположенных в колонках 1 и 3. Поскольку состояния 1, 3, 6 и 8 отмечены пустой буквой e, то и состояния 1 v 3, 3 v 6, 3 v 8 также отмечаются буквой е.

После построения таблицы проведем второй этап минимизации числа внутренних состояний автомата. Можно объединить состояния, отмеченные индексами: 0 и 1v3, 4 и 3v6, 5 и 3v8. При этом состояния отмеченные звездочкой обозначим через 10, а состояния 1v3 – 0, 3v6 – 4, 3v8 – 5.

yg	e	e	y3	e	e	e	e	y1	e	y2	e
xj\ai
xr
X01
X10
xs

По построенной таблице проведем третий этап минимизации, исключив такие состояния, в которые автомат из нулевого состояния никогда перейти не может. В нашем случае такими состояниями являются 1, 3, 6, 8 и 10.

Обозначив оставшиеся состояния 0 – b ₀, 2 – b ₁, 4 – b ₂, 5 – b ₃, 7 – b ₄, 9 – b ₅, получим окончательную таблицу переходов заданного автомата.

yg	e	y3	e	e	y1	y2
xj\ai	b0	b1	b2	b3	b4	b5
xr	b0	b0	b2	b3	b0	b0
x01	b2	b2	b2	b2	b2	b2
x10	b3	b3	b3	b3	b3	b3
xs	b1	b1	b4	b5	b1	b1

Дата добавления: 2014-10-31