Растворы электролитов

При растворении электролита в воде увеличивается общее число частиц, т. к. электролиты диссоциируют на ионы и наблюдается отклонение от законов Вант-Гоффа и Рауля.

Это отклонение характеризуется изотоническим коэффициентом i, который показывает, во сколько раз осмотическое давление р_осм, повышение температуры кипения Dt_кип, понижение температуры замерзания Dt’_зам электролита, найденные экспериментально, больше соответствующих значений (P_осм, Dt_кип, Dt’_зам)для растворов неэлектролитов при той же молярной концентрации или моляльности.

Значение изотонического коэффициента для растворов электролитов больше 1, для растворов неэлектролитов равно 1.

Осмотическое давление для растворов электролитов с учетом изотонического коэффициента

P_осм = i×n×R×T/V=i×T×R × С_М.

2-й закон Рауля для растворов сильных электролитов выражается уравнениями

Dt_кип= i×m₁×К_э×1000/М×m₂ и Dt_зам= i×m₁×К_к×1000/М×m₂.

Изменение общего числа частиц в растворах электролитов характеризуется степенью электролитической диссоциации a.

Степень диссоциации и изотонический коэффициент электролита связаны между собой соотношением

a = i –1 / k-1,

где k – число ионов, образующихся при диссоциации молекулы вещества.

В зависимости от степени диссоциации различают электролиты сильные и слабые. Электролиты, диссоциированные на 30 % и больше, обычно называют сильными, диссоциированные в пределах от 30 до 3 % – электролитами средней силы, еще менее диссоциированные – слабыми электролитами.

Согласно новой электростатической теории электролитов, сильные электролиты в разбавленных растворах нацело диссоциированы на ионы, т.е. степень диссоциации a = 1. Однако степень диссоциации определяется экспериментально и оказывается, как правило, меньше единицы (a < 1). Объясняется это тем, что измеряется всегда не истинная, а кажущаяся степень диссоциации. Так, если a = 0,7, то все молекулы диссоциированы на ионы, но ионы свободны лишь на 70 %, остальные 30 % ионов «связаны» электростатическими взаимодействиями.

Слабые электролиты диссоциируют в растворах не полностью. В их растворах устанавливается равновесие между недиссоциированными мо­лекулами и продуктами их диссоциации - ионами.

Степенью диссоциации a электролита называется доля его мо­лекул, подвергшихся диссоциации, т.е. отношение числа молекул, рас­павшихся на ионы, к общему числу растворенных молекул электролита:

,

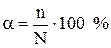где n –число молекул, распавшихся на ионы; N – общее число раст­воренных молекул.

В случае электролита АХ устанавливается равновесие

,

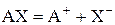константа которого (константа диссоциации) определяется соотношением

.

Для бинарного электролита АХ константа и степень диссоциации свя­заны соотношением (закон разбавления Оствальда):

К_д = С_М × a²/1-a,

где С_м – молярная концентрация электролита, моль/л.

Так как для слабых электролитов степень диссоциации значительно меньше единицы, то для приближенных расчетов можно принять 1 - a» 1. Тогда выражение закона Оствальда упрощается:

К_д = С_М × a², откуда

.

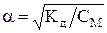Если в растворе электролита АХ степень его диссоциации равна a, то концентрации ионов А⁺ и 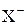в растворе одинаковы и могут быть найдены по формуле [А⁺] = [Х^-] = a × С_М.

Подставив значение a из выражения закона разбавления, находим

[А⁺] = [] = .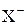

Задача 732

Раствор, содержащий 2,1 г гидроксида калия в 250 г воды, кристаллизуется при 0,52 °С. Определить кажущуюся степень диссоциации КОН (= 1,86).

Решение:

Находим понижение температуры замерзания раствора без учета диссоциации электролита (∆t_{зам. выч.}):

Dt_{зам. выч.} = К_к× m₁×1000/М×m₂ = 1,86×2,1×1000/56×250 = 0,28 °С.

Вычисляем изотонический коэффициент:

.

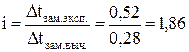Находим кажущуюся степень диссоциации: КОН = К ⁺ + ОН^– (k = 2),

a = i-1/k-1 = 1,86-1/2-1 = 0,86 или 86 %.

Задача 746. Кажущаяся степень диссоциации карбоната натрия в растворе, содержащем 1,06 г Nа₂СО₃ в 200 г H₂O, равна 0,70. Определить температуру замерзания этого раствора (= 1,86°).

Решение:

Находим изотонический коэффициент i из формулы

a = i-1/k-1, i = 1+a(k-1).

Na₂CO₃ = 2 Na⁺+ СО₃^2– (k = 3, a = 0,70 в долях единицы, = 106 г/моль),

i=1 + 0,7× (3-1) = 2,4.

Вычисляем понижение температуры замерзания раствора

,

Dt_{зам р-ра}= Dt_{зам воды} - Dt_зам=0-0,22=-0,22°С.

Задача 757. Раствор, содержащий 10 г хлорида натрия в 100 г воды, кипит при температуре 101,6 ^oC. Определить кажущуюся степень диссоциации NaCl
(= 0,516°).

Решение:

Находим повышение температуры кипения раствора без учета диссоциации электролита (∆t_{кип. выч.}):

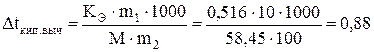^oC,

t_{кип. р-ра} = t_{кип. р-теля} + ∆t_кип; ∆t_{кип. эксп} = 101,6^o – 100^o = 1,6^o.

Вычисляем изотонический коэффициент:

.

Находим кажущуюся степень диссоциации: NaCl = Na⁺ + Cl^– (k = 2)

или 82 %.

Задача 773

Найти степень диссоциации и концентрацию ионов Н⁺ сероводородной кислоты по первой ступени в 0,1М растворе, если константа диссоциации для этой ступени равна 1,1×10^-7.

Решение:

Сероводородная кислота очень слабая, диссо­циирует по уравнению

H₂S = Н⁺ + HS^–.

Используя упрощенное выражение закона разбавления Оствальда, вычисляем степень диссоциации:

;

a = 1,05×10^-3×100 = 0,105 %.

Концентрация ионов [Н⁺] = С_м × a = 0,1×1,05×10^–3 = 1,05×10^–4 моль/л.

В задачах 729–744 определить кажущуюся степень диссоциации электролитов по температуре замерзания раствора

№	Электролит	Содержание воды, г	Температура замерзания раствора,^оС
Формула	Содержание
729. 730. 731. 732. 733. 734. 735. 736. 737. 738. 739. 740. 741. 742. 743. 744.	МgС12 ZnCI2 Nа2СО3 КОН KCI NaCI MgCl2 СаC12 А12(SO4)3 АgNO3 KNO3 НCI NaCI СаC12 СН3СООН NaCI	3 г 0,85 г 0,53 г 2,1 г 4,47 г 14,62 г 0,1 моль 0,745 г 8 г 6,8 1моль 1,246 г 3г 0,117 моль 0,66 г 0,3668 г	1л	-1,23 -0,23 -0,13 -0,52 -2,0 -1,67 -0,461 -0,36 -4,46 -0,337 -3,01 -1,18 -1,8 -0,6 -0,21 -0,22

В задачах 745–756 вычислить температуру замерзания водных растворов электролитов

№	Растворенное вещество	Содержание растворителя, г	Кажущаяся степень диссоциации, (%, долей единиц)
Формула	Содержание
745. 746. 747. 748. 749. 750. 751. 752. 753. 754. 755. 756.	СаС12 Na2CO3 AgNO3 KCI Na2SO4 СаС12 NaCI NaОН МgС12 MgSO4 NaNO3 KCI	0,666 г 1,06 г 1 г 2,33 г 3,55 г 8 г 2 моль 100 г 0,1 н 0,01 н 0,1 моль 0,1 н	500 мл - - -	0,75 0,7 0,59 0,8 70 % 70 % 70 % 60 % 0,75 66 % 80 % 0,8

В задачах 757–771 определить кажущуюся степень диссоциации водных растворов электролитов по их температурам кипения

№	Электролит	Содержание, г/100 Н2O	Температура кипения, °С
757. 758. 759. 760. 761. 762. 763. 764. 765. 766. 767. 768. 769. 770. 771.	NaCI NaNO3 KCI КNO3 MgCI2 MgSO4 NH4CI NH4CO3 СаCI2 Ba(NO3)2 SrCI2 ZnSO4 KNO3 NаOH NаOH	4,11 2,05	101,6 101,1 101,1 101,7 102,2 101,6 101,5 102,5 105,0 101,0 102,5 101,0 100,4 100,184 100,5

В задачах 772–788 вычислить степень диссоциации и концентрацию ионов водорода в растворах слабых электролитов по величине их констант диссоциации. Данные констант диссоциации взять из табл. 9 приложения

№ задачи	Электролит	Концентрация р-ра, моль/л	№ задачи	Электролит	Концентр. р-ра, моль/л
772. 773. 774. 775. 776. 777. 778. 779. 780.	HF H2S HCN СН3СООН HNO2 Н3РO4 HCN H2О2 НСООН	0,5 0,1 0,1 0,5 0,01 0,5 1,00 0,01		Н3ВO3 Н2SO3 Н2С2O4 Н2CO3 H2S СН3СООН Н3РO4 NН4ОН	0,05 0,01 0,05 0,1 0,2 0,05 0,01 0,02

Дата добавления: 2014-10-31