Потенциальная энергия – это энергия, которой обладает тело в поле!

Если тело движется в каком-либо поле, то оно обладает одновременно и кинетической и потенциальной энергией. Полной механической энергией тела называется сумма его кинетической и потенциальной энергий:

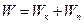. (3.8)

Если тело совершает работу, то , т. е. работа, совершаемая телом, равна разности полной энергии в начальном и конечном состояниях.

Если добавить к полной механической внутреннюю энергию тела (энергию теплового хаотического движения атомов и молекул, из которых состоит само тело) и тепловую, которую теряет тело, например при ударе, то мы получим полную энергию тела: 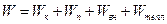. (3.9)

В замкнутой системе (система, в которой тела взаимодействуют только друг с другом и никакие внешние силы на систему не действуют) справедлив закон сохранения полной энергии: полная энергия в замкнутой системе ниоткуда не возникает, никуда не исчезает, а только может превращаться из одних видов в другие или может быть израсходована на совершение работы.

Если в механической системе действуют только консервативные силы (сила тяжести, сила упругости), то для нее выполняется закон сохранения механической энергии: 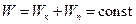. (3.10)

Т.е.: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, есть величина постоянная.

В такой системе может происходить только превращение потенциальной энергии в кинетическую и обратно, но полный запас энергии при этом не изменяется.

Если же в системе, кроме консервативных сил, действуют еще и неконсервативные силы (силы трения), то полная механическая энергия не сохраняется. Работа неконсервативных сил А_н.к.= W ₂ – W ₁ (3.11)

равна уменьшению энергии системы.

Для неконсервативных сил применяется также другое название – диссипативные силы. А сам процесс убыли энергии (например, под действием силы трения) называется диссипацией энергии. Говорят, что энергия диссипирует в окружающую среду. А сами системы, в которых энергия не сохраняется, называются диссипативными.

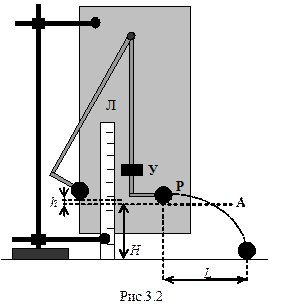Экспериментальная установка для проверки закона сохранения механической энергии показана на рис.3.2.

При отклонении шарика на высоту h относительно уровня А его полная энергия будет равна потенциальной: . (3.12)

При движении стержня с шариком до положения равновесия Р, потенциальная энергия превращается в кинетическую энергию поступательного движения тела: . (3.13)

При ударе стержня об упор У шарик срывается со стержня и движется по параболе. Измеряя дальность полета L и высоту падения шарика H, можно найти его скорость в момент отрыва от стержня – в точке Р.

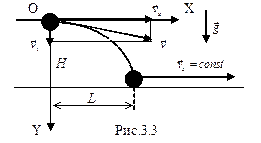Спроектируем вектор скорости в момент отрыва шарика от стержня на оси OX и OY (Рис.3.3). Учтем, что на шарик действует только сила тяжести, направленное вертикально вниз (вдоль оси OY). Поэтому, будет увеличиваться только игрековая компонента скорости . При этом, движение вдоль оси OY будет равноускоренным. Вдоль оси ОХ ускорение равно нулю, поэтому, компонента скорости 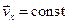будет оставаться постоянной и движение вдоль оси ОХ будет равномерным. Но скорость при равномерном движении вдоль оси ОХ можно найти по формуле (2.6): . (3.14)

Нам остается найти время полета. Для этого учтем, что нам известно расстояние, пройденное шариком вдоль оси OY – это высота H, с которой падает шарик. А расстояние, пройденное телом при равноускоренном движении вдоль оси OY, можно найти по формуле (2.8): .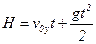

Учитывая, что начальная скорость вдоль оси OY в момент отрыва 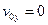, то уравнение для высоты полета: , откуда найдем время полета:

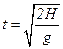. (3.15)

Подставляя время полета (3.15) в выражение скорости (3.14), получим:

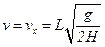. (3.16)

Подставляя скорость (3.16) в выражение кинетической энергии (3.13):

. (3.17)

Сравнивая значения потенциальной (3.12) и кинетической (3.17) энергий, можно экспериментально проверить закон сохранения механической энергии.

Дата добавления: 2014-10-31