Теория работы. Лабораторная работа №5. Определение коэффициента вязкости жидкости методом Стокса

Лабораторная работа №5. Определение коэффициента вязкости жидкости методом Стокса

Цель работы: изучить характеристики вязкой жидкости, научиться измерению вязкости жидкости методом Стокса.

Приборы и принадлежности: штатив, стеклянная трубка с машинным маслом, пипетка, стакан, секундомер, линейка, весы с разновесами.

При движении с различными скоростями слоев жидкости или газа между ними возникает трение, названное внутренним трением или вязкостью. В дополнение к этому между слоями молекул, смещающихся друг относительно друга, существуют силы взаимодействия. Сила внутреннего трения определяется из уравнения Ньютона: 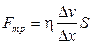,(5.1)

где h - коэффициент внутреннего трения или вязкости; D v/ D x - градиент скорости; S - площадь соприкасающихся слоев.

Сила внутреннего трения прямо пропорциональна градиенту скорости и площади соприкасающихся слоев.

Если выразить из (5.1) коэффициент вязкости h, то получим: ,

тогда коэффициент вязкости численно равен силе трения между слоями жидкости при единице площади их соприкосновения, если градиент скорости равен единице. В системе СИ единица измерения вязкости - Па×с (Па - паскаль):

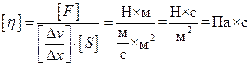
При небольшой скорости течения жидкость как бы разделяется на слои, которые скользят один относительно другого не перемешиваясь. Такое слоистое течение называется ламинарным. При движении тела в вязкой жидкости с небольшими скоростями обтекание тела жидкостью также будет ламинарным. В этом случае сила сопротивления движению тела со стороны жидкости определяется по закону Стокса. Для тела сферической формы:

F_с = 6 × p × h ×r×v,

где h - коэффициент вязкости, r - радиус тела, v - скорость движения тела в жидкости.

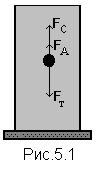При установившемся движении шарика плотностью r _ш в исследуемой жидкости плотностью r_ж на шарик действуют силы тяжести F _Т, сила сопротивления F _С и сила Архимеда F _А (Рис.5.1). По первому закону Ньютона при равномерном движении шарика в жидкости сумма всех действующих на него сил равна нулю:

F _Т - F _А – F _С = 0,

тогда: F _Т = F _А + F _С(5.2)

Учитывая, что масса шарика m= r_ш V, где V - объем шара, равный V= 4/3p r ³, где r - радиус шарика, получаем, что масса m= 4/3p r ³r_ш.

Тогда сила тяжести: F _Т =mg= 4/3p r ³r_ш g.

Сила сопротивления: F _С = 6ph rv, где v - скорость движения тела.

Архимедова сила: F _А = r_ж Vg= 4/3p r ³r_ж g.

Тогда выражение (5.2) принимает вид:

4/3p r ³r_ш g = 4/3 pr ³r_ж g + 6ph rv. (5.3)

Из выражения (5.3) определяем коэффициент вязкостиh:

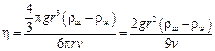. (5.4)

Если учесть, что диаметр шара d= 2 r, а скорость при равномерном движении определяется как 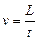, где L - расстояние, пройденное шариком за время t, то выражение для определения коэффициента вязкости (5.4) примет вид:

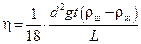. (5.5)

Представим теперь, что роль шариков, равномерно двигающихся в жидкости, играют эритроциты, осаждающиеся в плазме крови. Если выразить из (5.4) скорость движения шарика, то мы получим скорость СОЭ – скорость оседания эритроцитов!

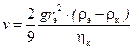(5.6)

Полученное выражение (5.6) поможет ответить на два очень важных в физиологии вопроса:

Дата добавления: 2014-10-31