Теория работы. Лабораторная работа №7. Определение размеров молекул касторового масла

Лабораторная работа №7. Определение размеров молекул касторового масла

Определение коэффициента поверхностного натяжения жидкости

1. Занесите в таблицу значение коэффициента жесткости пружины, вычисленное в задании №1.

2. Поднимите столик с сосудом А так, чтобы кольцо начало касаться поверхности жидкости. Заметьте начальное положение стрелки.

3. Медленно опускайте сосуд с жидкостью до момента отрыва кольца, глядя на положение стрелки Д. (Особенно важно точно заметить, куда на шкале М показывает стрелка в момент отрыва кольца).

4. Вычислите дополнительное удлинение пружины Dl, обусловленное силой поверхностного натяжения.

5. Измерьте с помощью штангенциркуля внешний и внутренний диаметры кольца d ₁ и d ₂.

6. По формуле (6.12) вычислите коэффициент поверхностного натяжения жидкости.

7. Опыт повторите не менее 5 раз.

8. Рассчитайте погрешность измерений.

9. Сравните полученный результат с табличным: σ(H₂O) = 0,073 Н/м.

10. Результаты измерений и вычислений занесите в таблицу.

k =
№	D l, м	d 1, м	d 2, м	σ, Н/м	<σ>, Н/м	Δσ, Н/м	<Δσ>, Н/м	ε, %
σ =±

Вычисления к заданию №2:

Вывод:

Контрольные вопросы защиты лабораторной работы:

1. Что такое жидкость? На основании рис. 6.1 и 6.2 объясните причину возникновения внутреннего давления в жидкости. Что такое внутреннее давление? Почему жидкость является практически не сжимаемой?

2. На основании рис. 6.3 и 6.4 объясните причину возникновения поверхностного натяжения. Что такое сила и коэффициент поверхностного натяжения с точки зрения силы и свободной энергии? Сделайте вывод формулы (6.7).

3. На основании рис.6.6 объясните метод отрыва кольца, сделайте вывод расчетной формулы (6.12).

Цель работы: изучить явления смачивания и не смачивания, понять механизм возникновения газовой эмболии, определить диаметр и высоту молекулы касторового масла.

Приборы и принадлежности: ванночка, стеклянная палочка, пипетка, линейка, химический стаканчик, весы, разновесы, касторовое масло, марганцовка.

При взаимодействии жидкости с поверхностью твёрдого тела могут возникать два типа явлений.

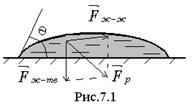Смачивание (Рис.7.1) – это явление, при котором сила взаимодействия между молекулами жидкости и молекулами твёрдого тела(F_ж-тв ) больше, чем сила взаимодействия молекул жидкости между собой (F_ж-ж ).

Тогда результирующая сила F_р направлена в сторону твердого тела и заставляет жидкость растекаться по поверхности твердого тела. Кривизна поверхности жидкости характеризуется краевым углом q (греч. «тета») – это угол между твёрдым телом и касательной к поверхности жидкости и отсчитываемый внутри жидкости. При смачивании краевой угол острый, т.е. лежит в пределах 0 < θ ≤ 90°. Если θ= 0°, то такое явление называется полным смачиванием (это идеализированный предельный случай, при котором жидкость должна растечься в мономолекулярный слой).

Несмачивание (Рис.7.2) – это явление, при котором силы взаимодействия молекул жидкости и молекул твёрдого тела меньше чем, силы взаимодействия молекул жидкости между собой.

При несмачивании краевой угол тупой и лежит в интервале 90°<θ≤180°.Если θ = 180°, то такое явление называется полным несмачиванием. В случае полного несмачивания жидкость практически должна соприкасаться с поверхностью твердого тела всего лишь одной молекулой, что в Земных условиях при действии силы тяжести невозможно.

Одна и та же жидкость может смачивать одну поверхность, а другую поверхность не смачивать. Например, вода смачивает стекло и не смачивает жиры; лист растения не смачивается водой, т. к. покрыт воскообразной смазкой.

За счёт смачивания и не смачивания жидкость, налитая в сосуд, будет иметь вид, представленный на рис.7.3.

Рассмотрим молекулу, находящуюся на поверхности жидкости.

На молекулу в поверхностном слое действуют силы притяжения со стороны соседних молекул – силы поверхностного натяжения, но сумма всех сил, действующих на молекулу уже не равна нулю, как в случае ровной поверхности. Под действием некомпенсированных сил поверхностного натяжения возникает результирующая сила, направленная при смачивании наружу, при не смачивании – внутрь жидкости.

Если найти отношение результирующей силы, действующей на молекулы, к площади поверхности жидкости, то получим Δ р – дополнительное давление, возникающее в жидкости. Величину дополнительного давления можно определить по формуле Лапласа: 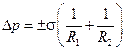, (7.1)

где σ – коэффициент поверхностного натяжения; R ₁ и R ₂ – радиусы кривизны поверхности жидкости во взаимно перпендикулярных плоскостях.

Если поверхность жидкости сферическая, то радиусы кривизны поверхности во взаимно перпендикулярных направлениях одинаковы R ₁ = R ₂ = R. Тогда формула Лапласа примет более простой вид: 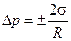. (7.2)

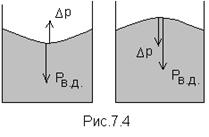Возникает естественный вопрос: почему дополнительное давление называется дополнительным давлением? Оно имеет такое название, потому что дополняет внутренне давление, направленное всегда в глубь жидкости (Рис.7.4). Поэтому при смачивании дополнительное давление Δ р направлено противоположно внутреннему давлению, чему в формуле Лапласа соответствует знак «-». При не смачивании дополнительное давление Δ р направлено в одну сторону с внутренним давлением, чему в формуле Лапласа соответствует знак «+».

Пусть в узкой трубке с жидкостью (капилляре) движется пузырёк воздуха (например, пузырек воздуха попал в кровеносную систему). И пусть, этот пузырек воздуха под действием течения крови, т.е. под действием давления крови р_кр. попал на разветвление более мелких кровеносных сосудов (Рис.7.5). Кровь смачивает стенки кровеносного сосуда, поэтому возникает вогнутая поверхность и, как следствие, дополнительное давление. Из формулы (7.2) видно, что, чем меньше радиус сосуда, тем больше дополнительное давлениеΔ р в пузырьке воздуха. Поэтому, в капилляре большего радиуса возникает дополнительное давление Δ р ₁ меньшее, чем в более мелких капиллярах Δ р ₂. В зависимости от радиусов более мелких капилляров может возникнуть ситуация, когда сумма давления крови и дополнительного давления Δ р ₁станет меньше, чем суммарное дополнительное давление со стороны поверхностей в более мелких капиллярах, направленное противоположно течению крови. Давления крови окажется недостаточно, чтобы «протолкнуть» или «разорвать» этот пузырек воздуха. Произойдет закупорка – тромбирование кровеносного сосуда, называемая газовая эмболия, что может привести к летальному исходу для человека или животного. На основании рассмотренного явления – газовой эмболии становится понятно, почему очень важно выпускать все пузырьки воздуха при проведении внутримышечных и, особенно, внутривенных инъекций.

В отличие от газа или пара, которые всегда целиком заполняют предоставляемый им объем, жидкости образуют свободную поверхность, отделяющую данную жидкость от пограничной среды. В поверхностном слое действуют силы поверхностного натяжения.

Под действием сил поверхностного натяжения свободная поверхность жидкости стремится стать сферической. Обычно этому препятствует сила тяжести, под действием которой жидкость принимает форму того сосуда, в котором находится, а свободная поверхность делается горизонтальной.

Однако когда силы поверхностного натяжения значительно превосходят силу тяжести, свободная поверхность жидкости приближается к сферической.

Рассмотрим каплю некоторой жидкости 1, расположенную на поверхности другой, не смешивающейся с ней жидкости 2 (Рис.7.5).

Форма капли устанавливается в данном случае под влиянием взаимодействия трех сред: жидкости 1, жидкости 2 и воздуха 3. Эти среды имеют общую границу - окружность, ограничивающую каплю и пересекающую плоскость чертежа в двух точках А и В. По этой окружности пересекаются между собой три поверхности:

· поверхность, ограничивающая жидкость 2 и воздух, вдоль которой действует сила поверхностного натяжения F ₂₃ с коэффициентом поверхностного натяжения σ₂₃;

· поверхность, разграничивающая каплю жидкости 1 и воздух, вдоль которой действует сила поверхностного натяжения F ₁₃ с коэффициентом поверхностного натяжения σ₁₃;

· поверхность, разграничивающая жидкости 1 и 2, вдоль которой действует сила поверхностного натяжения F ₁₂ с коэффициентом поверхностного натяжения σ₁₂.

На каждую единицу длины пограничной окружности будут действовать три силы поверхностного натяжения - F ₂₃, F ₁₃, F _l2, прямо пропорциональные соответственно σ₂₃, σ₁₃, σ₁₂ . Эти силы будут направлены по касательной к соответствующим поверхностям раздела. В результате поверхность капли образует с поверхностью второй жидкости краевые углы q₁ и q₂.

В случае, когда силой тяжести по сравнению с силой поверхностного натяжения можно пренебречь, равновесной будет та форма капли, при которой векторная сумма всех сил поверхностного натяжения равна нулю:

.

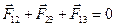Спроектируем силы поверхностного натяжения на горизонтальную поверхность второй жидкости и учтем, что силы F ₁₂ и F ₁₃ противоположны F ₂₃, тогда: F ₂₃ = F ₁₃ cosq₁₃ + F ₁₂ cosq₁₂. (7.3)

Отсюда следует, что для того, чтобы капля жидкости не растекалась, т.е. находилась в состоянии равновесия, необходимо, чтобы выполнялось условие:

F ₂₃ £ F ₁₃ cosq₁₃ + F ₁₂ cosq_12. (7.4)

Т.е., чтобы сила поверхностного натяжения, действующая на каплю со стороны поверхности раздела «вторая жидкость-воздух» была меньше чем сумма двух других сил поверхностного натяжения, действующих на каплю на границах раздела «капля-вторая жидкость» и «капля-воздух».

Но, учитывая, что сила поверхностного натяжения (6.6) прямо пропорциональна длине границе раздела между средами 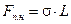, то, подставляя ее в неравенство (7.4), получим неравенство, при котором капля жидкости не будет растекаться на поверхности второй жидкости:

. (7.5)

Т.е. капля не будет растекаться, если коэффициент поверхностного натяжения второй жидкости меньше, чем сумма коэффициентов поверхностного натяжения капли на ее границах раздела с воздухом и со второй жидкостью.

И наоборот, если неравенство (7.5) не выполняется, т.е.:

, (7.6)

то капля будет растекаться по поверхности второй жидкости в виде пленки (силы поверхностного натяжения, действующие со стороны поверхности второй жидкости будут как бы «разрывать» каплю).

Многие органические жидкости (эфир, скипидар, керосин) растекаются по поверхности воды. Для некоторых жидкостей (бензол, жирные кислоты масла) растекание наблюдается для первых капель, помещенных на поверхность чистой воды. Последующие капли уже не растекаются, а остаются на поверхности в виде устойчивых капель из-за того, что первые капли, растекаясь, достаточно уменьшают поверхностное натяжение. Таким образом, растворяя даже небольшое количество примесей в растворителе, можно влиять на его коэффициент поверхностного натяжения и, следовательно, «управлять» процессом растекания или не растекания по его поверхности других жидкостей.

Ленгмюр и Дево предложили метод определения размеров молекул касторового масла, основанный на растекании капли масла по поверхности воды.

Экспериментально установлено, что если поверхность воды достаточно велика, то капля масла соответствующего объема растекается в очень тонкий мономолекулярный слой, т.е. слой толщиной в одну молекулу. Если капля касторового масла упадет на поверхность воды, закрашенной марганцовкой, то, растекшись по ней, она становится хорошо видна.

Растекшись по поверхности воды, капля касторового масла в идеальном случае принимает форму круглого пятна площадью S (Рис.7.6). Измерив линейкой диаметр образовавшегося круглого пятна D, можно найти площадь его поверхности:

. (7.7)

Молекулу масла (жирных кислот) можно рассматривать как образование, сильно вытянутое в длину, нечто вроде цилиндра. Форму молекулы масла будем считать цилиндрической. Тогда площадь кругового поперечного сечения молекулы: 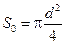, (7.8)

где d - диаметр молекулы касторового масла.

В мономолекулярном слое молекулы масла расположены вертикально. Предполагая, что молекулы масла плотно расположены в мономолекулярном слое, как на рис 7.6, можно найти число молекул в мономолекулярном слое, используя выражения (7.7) и (7.8): . (7.9)

Но, с другой стороны, число молекул в капле мы можем найти как произведение числа молей 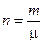на число Авогадро – число молекул в одном моле N_A =6,02·l0²³ моль^-1, т.е. 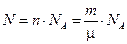, (7.10)

где m – масса капли; m=0,894 кг/моль – молярная масса касторового масла.

Приравнивая (7.9) и (7.10), получим: . Откуда выразим диаметр молекулы касторового масла: . (7.11)

Высота молекулы равна толщине мономолекулярного слоя. А толщину цилиндрического слоя мы можем найти из его объема: 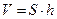. Тогда:

. (7.12)

Но объем капли касторового масла можно найти, зная массу m капли и плотность масла r = 970 кг/м³: . (7.13)

Подставляя (7.13) и (7.7) в (7.12), получим высоту молекулы – толщину мономолекулярного слоя: 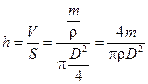. (7.14)

Дата добавления: 2014-10-31