Жидкость является несжимаемой, потому что уже сжата под действием огромного внутреннего давления!

Если создать давление, превышающее внутреннее, то жидкость можно сжимать, но это очень сложная научная и техническая задача. Поэтому, при рассмотрении реальных жидкостей в наших «обычных» бытовых условиях, мы можем их считать несжимаемыми и пользоваться для описания движения уравнениями гидродинамики идеальной (т.е. несжимаемой) жидкости.

Для пытливого ума, естественно, возникает вопрос: а что будет, если удастся создать внешнее давление, превышающее внутреннее? Действительно, такой вопрос стоит перед наукой. Существует Теория металлического водорода! Действительно, если жидкий водород продолжать сжимать, то произойдет перекрытие электронных орбиталей, «лишние» электроны должны будут уйти из электронных облаков, т.е. станут коллективизированными. Между атомами водорода должна «включиться» ковалентная химическая связь (а это очень прочная связь – как, например, в металлах, в кристалле алмаза). Т.е. жидкий водород должен превратиться в металл! Как все красиво! Но почему же до сих пор наука не смогла его получить? А вот почему. Когда мы создаем внешнее давление, то давим каким-нибудь поршнем. Поршень сделан из металла, размеры атомов которого велики. Соответственно, велики и межатомные расстояния. А водород – это первый и самый маленький из атомов в таблице Менделеева. Он, просто «просачивается» между атомами металла! Если удастся найти «чем давить», то, наверное, и удастся получить металлический водород.

Но мы с вами отвлеклись от дальнейшего изучения молекулярного строения 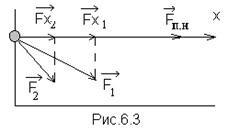жидкости.

Рассмотрим теперь молекулу, лежащую на краю поверхности жидкости (Рис.6.3) и спроектируем все силы на оси ОХ и OY. По-прежнему сумма проекций сил на ось OY даст нам силу внутреннего давления, и о ней мы больше говорить не будем. Но вот теперь, сумма проекций сил на ось ОХ тоже не равна нулю (потому что справа от нашей молекулы есть «соседи», притягивающие ее, а слева – нет). Такая результирующая сила называется силой поверхностного натяжения – это сила, с которой молекулы, находящиеся на краю поверхности жидкости, действуют на молекулы, лежащие в глубине поверхности.

Нальем, например, жидкость в сосуд цилиндрической формы и посмотрим на него сверху (Рис.6.4). Молекулы жидкости, лежащие на краю поверхности, будут создавать силу поверхностного натяжения, которая будет стремиться «сжать» поверхность. Таким образом, сила поверхностного натяжения действует по касательной к поверхности жидкости перпендикулярно контуру, ограничивающему поверхность жидкости.

При перемещении молекул из поверхностного слоя вглубь жидкости или, наоборот, из глубины жидкости на поверхность совершается работа. Эта работа тем больше, чем больше различие между силами взаимодействия молекул поверхностного слоя с молекулами жидкости и молекулами граничащей среды.

Рассмотрим жидкость, граничащую со своим паром. Концентрация молекул в воздухе и паре намного меньше, чем в жидкости. Поэтому на молекулы поверхностного слоя жидкости действует сила, направленная внутрь жидкости. Предположим теперь, что площадь поверхности жидкости при изотермическом обратимом процессе увеличилась на величину dS. Это значит, что некоторое количество молекул перешло из глубины жидкости в поверхностный слой. Следовательно, внешними силами совершена некоторая работа d А, которая прямо пропорциональна количеству молекул, перешедших в поверхностный слой, а значит, и увеличению площади поверхности жидкости на dS: d А =s dS, (6.1)

где s - (греч. «сигма») это коэффициент поверхностного натяжения.

Из (6.1) следует, что коэффициент поверхностного натяжения определяется работой, необходимой для изотермического обратимого увеличения площади поверхности на единицу.

Поскольку работа при изотермическом обратимом процессе равна изменению свободной энергии системы (d А = dЕ), то избыточная потенциальная энергия поверхности жидкости является ее свободной энергией dЕ. Тогда коэффициент поверхностного натяжения можно определить как свободную энергию единицы площади поверхности жидкости:

или . (6.2)

В состоянии устойчивого равновесия свободная энергия любой системы минимальна. Следовательно, в равновесии жидкость имеет минимальную площадь поверхности. Это значит, что должны существовать силы, стремящиеся сократить поверхность жидкости. Они направлены по касательной к поверхности жидкости.

Если проволочную рамку, одна из сторон АВ которой подвижна (Рис. 6.5), поместить в мыльный раствор и затем вынуть из него, то вся рамка затянется пленкой жидкости. Силы поверхностного натяжения принуждают пленку сокращаться и перемещают перемычку АВ. Чтобы ее удержать в равновесии, необходимо приложить внешнюю силу F. Так как пленка имеет две поверхности, вдоль каждой из которых действует сила поверхностного натяжения F_п.н, то: F= 2 F_п.н (6.3)

Предположим, что при постоянной температуре бесконечно медленно перемычка АВ перемещается на расстояние dx (Рис. 6.5). При этом внешняя сила совершает работу: d А =2 F_п.н dx. (6.4)

Эта работа пойдет на увеличение свободной энергии поверхности пленки:

d А = dE = s dS = s2 Ldx, (6.5)

где L - длина перемычки АВ или длина контура, ограничивающего поверхностный слой. Тогда из (6.4) и (6.5) получим, что сила поверхностного натяжения:

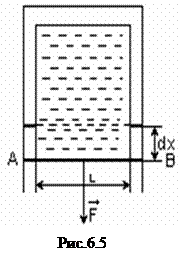
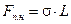. (6.6)

Сила поверхностного натяжения прямо пропорциональна длине контура, ограничивающего поверхность жидкости.

Из (6.6) выразим коэффициент поверхностного натяжения:

. (6.7)

В лабораторно-клинической практике по коэффициенту поверхностного натяжения определяют содержание желчных пигментов в моче. При их повышенном содержании коэффициент поверхностного натяжения s резко уменьшается.

Коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, с которой молекулы, лежащие на границе, действуют на единицу длины контура, ограничивающего поверхность жидкости.

Размерность коэффициента поверхностного натяжения: .

Дата добавления: 2014-10-31