Полиномиальная аппроксимация

Общие понятия

АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК НЭ

Аппроксимация нелинейной характеристики – замена истинной (экспериментально полученной) характеристики приближенно представляющей ее функцией.

Необходимость аппроксимации возникает при анализе, синтезе и расчете нелинейных цепей. Для упрощения аппроксимируют не всю характеристику НЭ, а только ее рабочий участок (используемую часть).

Различают способы аппроксимации:

- полиномиальная;

- кусочно-линейная;

- с помощью трансцендентных функций.

Выбор способа аппроксимации зависит от вида нелинейной характеристики, а также от режима работы НЭ. Выбранный способ аппроксимации должен обеспечивать достаточные полноту описания свойств НЭ, простоту математической обработки полученного представления характеристики и точность расчета.

График характеристики НЭ будем показывать сплошной линией, а график аппроксимирующей функции – штриховой.

Является одним из наиболее распространенных способов аппроксимации. Заключается в представлении нелинейной характеристики в виде полинома (многочлена) n-ой степени относительно рабочей точки (x₀, y₀):

,

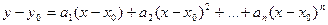где 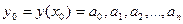- коэффициенты полинома. Зависят от положения рабочей точки на характеристике;

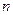- порядок полинома. Определяется требуемой точностью расчетов.

Примеры:

1) Полином второй степени:

-

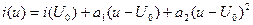- используется, если рабочая точка (определяется постоянным напряжением 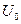) расположена на начальном участке характеристики, имеющем вид квадратичной параболы, и подводимое к НЭ напряжение сигнала не выходит за начало характеристики (за точку 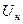, которая определяется из условия: i(U_н)=0).

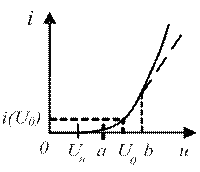
Рисунок 15.1 – Характеристика, для аппроксимации которой требуется полином второй степени. Используемые обозначения:

- i (U₀) – ток покоя;

- (a, b) – используемый участок ВАХ.

2) Неполный полином третьей степени:

-

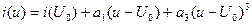- используется, если рабочая точка является точкой перегиба характеристики и напряжение сигнала не выходит за пределы напряжения насыщения + U_max.

Рисунок 15.2 – Характеристика, для аппроксимации которой требуется полином третьей степени.

3) Полином высокой (пятой и более) степени используется, если рабочая точка находится на нижнем сгибе характеристики и изменение напряжения сигнала велико.

Рисунок 15.3 – Характеристика, для аппроксимации которой требуется полином высокой степени.

Дата добавления: 2014-10-31