Полярная система координат

Говорят, что на плоскости введена полярная система координат, если заданы:

1) некоторая точка 0, называемая полюсом;

2) некоторый луч, исходящий из точки 0 и называемый полярной осью.

Полярными координатами точки M называются два числа: полярный радиус 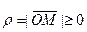и полярный угол - угол между полярной осью и вектором .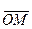

Пусть на плоскости введены декартова и полярная системы координат, причем начало декартовой системы совпадает с полюсом, а полярная ось - с положительной полуосью абсцисс. Тогда прямоугольные координаты x, y точки М и ее полярные координаты ρ, φ связаны следующими формулами:

,

,

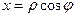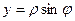
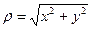Задание 4. Линия задана уравнением в полярной системе координат. Требуется:

1. Построить линию по точкам, придавая φ значения от до 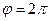через промежуток .

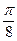2. Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.

3. По уравнению в декартовой прямоугольной системе координат определить тип линии.

Решение.

1) Совместим декартову и полярную системы координат и рассмотрим окружность произвольного, достаточно большого радиуса с центром в полюсе. Построим радиусы, образующие углы с полярной осью, где принимает значения от до 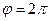с шагом 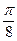. Вычислим косинусы этих углов и по этим значениям найдем 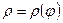. Результаты вычислений занесем в таблицу:

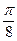
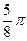
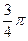
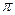
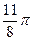
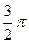
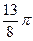
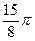
		0,92	0,7	0,38		-0,38	-0,7	-0,92	-1	-0,92	-0,7	-0,38		0,38	0,7	0,92
	0,16	0,17	0,19	0,24	0,33	0,53	1,11	4,16	∞	4,16	1,11	0,53	0,33	0,24	0,19	0,17	0,16

Построим точки () и по полученным точкам построим искомую линию:

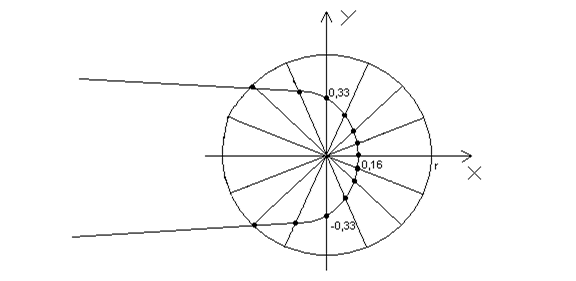
2) Найдем уравнение данной линии в декартовой системе координат. Для этого воспользуемся формулами:

.

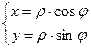Отсюда , .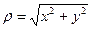

Тогда имеем:

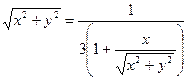
или после упрощения

.

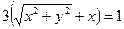3) Чтобы определить тип линии, определяемой полученным уравнением,

преобразуем его к каноническому виду:

или

.

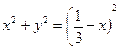Окончательно получим:

,

где ,. Таким образом, данное уравнение определяет параболу.

Дата добавления: 2014-10-15