Некоторые особые случаи пересечения поверхностей

В некоторых случаях расположение, форма или соотноше­ния размеров криволинейных поверхностей таковы, что для изображения линии их пересечения никаких сложных построе­ний не требуется. К ним относятся пересечения цилиндров с параллельными образующими, конусов с общей вершиной, соосных поверхностей вращения, поверхностей вращения, описанных вокруг одной сферы.

Изображения пересечения цилиндров с параллельными об­разующими приведены на рисунке 10.10 слева, конусов с об­щей вершиной — справа.

Соосные поверхности вращения. Изображения пересечений соосно расположенных различных поверхностей вращения при­ведены на рис. 10.11. Конус, пересекающийся с двумя цилин­драми разного диаметра (рис. 10.11, а), часто используют при конструировании как переход от одного диаметра к другому.

Конус, сопряженный со сферой, с переходом на цилиндры (рис. 10.11, б), широко используют в качестве деталей меха­низмов управления — рукояток.

Комбинацию из трех соосных пересекающихся конусов (рис. 10.11, <?) применяют при конструировании деталей, на­зываемых штифтами или роликами. Крайние конические по­верхности, называемые фасками, служат для упрочения кромки детали и предохранения тем самым от забоин основной рабо­чей конической поверхности. Комбинация из пересекающих­ся трех соосных конусов образует центровое гнездо для обработки деталей в центрах. Для предохранения от повреждений рабо­чей конической поверхности 1 при соприкосновении (ударах) с другими деталями служит наружный конус 2.

V ^б) Рис. 10.12 V

Пересечение поверхностей, описанных вокруг одной сферы (рис. 10.12). В этом случае линиями пересечения поверхнос-

тей 2-го порядка являются две плоские кривые 2-го порядка, изображаемые на плоскости, параллельной осям поверхнос­тей, в виде прямолинейных отрезков. Выше уже были приве­дены некоторые примеры таких пересечений.

Другие примеры изображения линии пересечения поверх­ностей вращения, описанных вокруг одной сферы, рассмотре­ны на рисунке 10.12.

В случаях, показанных на рис. 10.12 а, б, поверхности двух цилиндров, конуса и цилиндра пересекаются по двум эллип­сам с проекциями 1'2' и 3'4'.

В случае, показанном на рис. 10.12, в, пересечения кону­сов с вершинами S\ и S₂, у которых имеются две параллельные образующие, линии пересечения — эллипс с проекцией V2' и парабола с вершиной в точке с проекцией 3'.

Рассмотренные примеры пересечения двух поверхностей вращения, описанных вокруг одной сферы, являются частны­ми случаями, следующими из теоремы Монжа: две поверхнос­ти 2-го порядка, описанные около третьей поверхности 2-го порядка (или в нее вписанные), пересекаются между собой по двум кривым 2-го порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

Пересечение поверхностей, когда одна из них проецирую­щая (рис. 10.13). Если одна из пересекающихся поверхнос­тей проецирующая, то задача построения линии пересечения двух поверхностей упрощается и сводится к построению недо­стающих проекций кривой линии на одной из поверхностей по одной заданной проекции линии (см. 8.3). На рисунке 10.13 горизонтальная проекция линии пересечения прямого кругового цилиндра и сферы совпадает с горизонтальной про­екцией цилиндра. Фронтальная и профильная проекции ли­нии построены по их принадлежности сфере с помощью проекций вспомогательных линий на сфере. Отметим харак­терные (опорные) точки линии пересечения, пользуясь гори­зонтальной проекцией. Высшая и низшая точки (их проекции 2', 2, 2" та Г, 1, V) лежат в плоскости симметрии фигуры, проходящей через центр сферы с проекциями о' о и ось ци­линдра с проекциями о\о\, о_х. Горизонтальная проекция плос­кости симметрии — прямая, проходящая через проекции о и о_{. В пересечении этой прямой с проекцией цилиндра от­мечаем горизонтальные проекции 2 и / высшей и низшей то­чек линии пересечения. Заметим, что точка 2 — ближайшая

к высшей точке сферы, а точка / — наиболее удаленная от нее. Точки 3 и 4 — крайние левая и правая на фронтальной и горизонтальной проекциях, их профильные проекции 3", 4" на проекциях образующих, совпадающих с проекцией оси цилиндра. Точки 5 и 6 находятся на главном меридиане сфе­ры, их фронтальные проекции 5'и 6'— на фронтальном очерке сферы, профильные 5" и 6" — на профильной проекции вер­тикальной оси сферы. Точки 7 и 8 — ближайшая к плоскости Via наиболее удаленная от нее, их фронтальные проекции 7' и 8'— на проекции оси цилиндра, а профильные 7"тл 8" — на крайних левой и правой проекциях образующих. Точки 9тл 10 имеют проекции 9'w. 10'на фронтальной проекции вертикаль­ной оси сферы, проекции 9" и 10" — на профильной проек­ции очерка сферы.

Рассмотренные особенности характерных точек позволяют легко проверить правильность построения линии пересечения поверхностей, если она построена по произвольно выбранным

точкам. В данном случае десяти точек достаточно для прове­дения плавных проекций линии пересечения. При необходи­мости может быть построено любое количество промежуточных точек.

Проекция /' низшей точки построена с помощью проек­ций параллели сферы. Проекция 2' высшей точки построена с помощью проекций окружности радиуса o'd' 'наповерхности сферы, плоскость которой параллельна плоскости V. Анало­гичные построения остальных проекций точек линии пересече­ния ясны из чертежа.

Построенные точки соединяют плавной линией с учетом особенностей их положения и видимости.

И

1. В чем заключается общий способ построения линии пересечения двух поверхностей?

2. Какие точки линии пересечения поверхностей называют характер­ными?

3. В каких случаях для построения линии пересечения одной поверх­ности другой рекомендуется применять вспомогательные секущие плоскости, параллельные плоскостям проекций?

4. В каких случаях возможно и целесообразно применять вспомогатель­ные секущие сферы?

5. По каким линиям пересекаются между собой:

а) цилиндрические поверхности, образующие которых параллельны
между собой;

б) конические поверхности с общей вершиной?

6. Какие линии пересечения получаются при взаимном пересечении двух поверхностей вращения, описанных вокруг общей для них сферы?

7. По каким линиям пересекаются между собой соосные поверхности вращения?

Глава одиннадцатая АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

При изложении настоящего курса для наглядного изображе­ния расположенных в пространстве относительно выбранных плос­костей проекций точек, линий, плоскостей, многогранников, сечений конической поверхности плоскостями использовались проекции, называемые аксонометрическими (от древнегреческого «аксон» — ось, «метрио» — измеряю) или аксонометрией (см_; рис. 1.22, 2.1, 3.2, 4.10, 7.3 и др.). Их часто используют для наглядного изображения конструкций приборов, машин на чер­теже, особенно на начальных этапах конструирования.

Способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, проецируется параллель­но на некоторую плоскость, принятую за плоскость аксономет­рических проекций (эту плоскость называют также картинной плоскостью).

При параллельном проецировании, если направление про­ецирования перпендикулярно к аксонометрической плоскости проекций, аксонометрическую проекцию называют прямоуголь­ной, если направление проецирования не перпендикулярно к плоскости проекций, аксонометрическую проекцию называют косоугольной. В прямоугольной аксонометрической проекции оси присоединенных прямоугольных координат располагают непараллельно плоскости аксонометрических проекций.

Применяемые в отечественной конструкторской докумен­тации аксонометрические проекции стандартизованы в ГОСТ 2.317-69.

Рассмотрим образование аксонометрической проекции на при­мере изображения параллелепипеда с квадратным основанием (рис. 11.1) путем последовательного преобразования его ортого­нальных проекций вместе с осями. При повороте параллелепи-

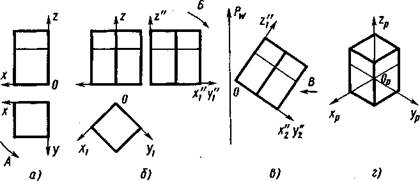
Рис. 11.1

педа (рис. 11.1, а) с осями дс и у вокруг оси z по стрелке А на 45° получаем его изображение (рис. 11.1, б) с повернутыми осями х_{ и yi и сохранившейся вертикальной осью z- При повороте изоб­ражения на профильной проекции с осями z", x'[, у'[ по стрелке Б на угол 30° получаем изображение (рис. 11.1, в) с осями z", *2, У'ъ расположенными под некоторыми углами к картинной плоскости P(P_W). Параллельная проекция (рис. 11.1, г) по стрелке В на плоскости Р и является аксонометрической проекцией па­раллелепипеда с осями на плоскости Р. Аксонометрическую плос­кость при этом не обозначают (ею является плоскость бумаги).

Проекции осей координат х_р, у_р, Zp на плоскости аксоно­метрических проекций называют аксонометрическими осями (в дальнейшем индекс «/?» будет опускаться).

При различном взаимном расположении осей координат в пространстве и плоскости аксонометрической проекции и при разных направлениях проецирования можно получить множество аксонометрических проекций, отличающихся друг от друга на­правлением аксонометрических осей и масштабами по ним. Это положение доказано теоремой К. Польке, которая утверждает:

три отрезка произвольной длины, лежащие в одной плоско­сти и выходящие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных от­резков, отложенных на прямоугольных осях координат от начала.

Рассмотрим направление аксонометрических осей и масш­табы по ним для направления проецирования, перпендикуляр­ного аксонометрической плоскости проекций, т. е. для прямоугольной аксонометрической проекции.

Коэффициент искажения. На рисунке 11.2 изображена про­странственная система ортогональных координат Ox, Oy, Oz,

единичные отрезки е на осях координат и их проекции в на­правлении S на некоторую плоскость Р, являющуюся аксоно­метрической плоскостью проекций. Проекции е_х, е_у, е_г отрезка е на соответствующих аксонометрических осях О_рх_р, О_ру_р, O_pZp в общем случае не равны отрезку е и не равны между собой. Отрезки е„ е_у, е_г являются единицами измерения по аксоно­метрическим осям — аксонометрическими единицами (аксо­нометрическими масштабами). Отношения

называют коэффициентами искажения по аксонометричес­ким осям.

В частном случае положение картинной плоскости можно выбрать таким, что аксонометрические единицы — отрезки е_х, е_у, е_г — будут все равны между собой или будет равна между собой пара этих отрезков.

При е_х = е_у= е_г (к=т=п) аксонометрическую проекцию называют изометрической; искажения по всем осям в ней оди­наковы. При равенстве аксонометрических единиц по двум осям, обычно при е_х = е_г * е_у (к = п * т), имеем диметричес-кую проекцию. Если е_х* е_у* е_г, то проекцию называют три-метрической.

Рис. 11.2 Рис. 11.3

Картинная плоскость Р на рисунке 11.3 изображена так, что она пересекает все три координатные оси Ох, Оу, Ozb точках х, у, z соответственно. Рассмотрим прямоугольную аксоно­метрию. В этом случае отрезок ОО_р перпендикулярен плоско­сти Р. Отрезки О_рх,-О_ру, O_pz являются аксонометрическими проекциями отрезков Ох, Оу, Oz и представляют собой ка­теты прямоугольных треугольников, гипотенузы которых —

отрезки Ох, Оу, Oz. Обозначим углы между осями координат и их проекциями на плоскости Р через а, р, у. Тогда

0„х О_ру O_pz

-^=cosa; ^=cosP; ^ = cosy.

Эти отношения являются коэффициентами искажения, т. е.

к — cos a; т = cos p; п = cos у.

Известно, что для отрезка ОО_рIP сумма квадратов направ­ляющих косинусов равна единице:

cos² (л/2 - a) + cos² (л/2 - Р) + cos² (л/2 - у) = 1.

Отсюда

sin² a + sin²p + sin²y = 1

или

1 — cos² a + 1 — cos²p + 1 — cos²y = 1.

Тогда

cos²a + cos²P + cos²y = 2

или

к² + m² + n² = 2,

т. е. сумма квадратов коэффициентов искажения равна 2.

Изометрическая проекция. В изометрической проекции все коэффициенты равны между собой:

к = т = п; к² + т² + п² — 2.

Тогда

Зк²=2,

откуда

к = Л/3 = 0,82.

Следовательно, при построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, умножают на 0,82. Такой перерасчет размеров неудобен. По­этому изометрическую проекцию для упрощения, как правило, вьшолняют без уменьшения размеров (искажения) по осям х, у, z, т. е. используют приведенный коэффициент искажения, который принимают равным 1. Получаемое при этом изображе­ние предмета в изометрической проекции имеет несколько боль-

шие размеры, чем в действительности. Увеличение в этом слу­чае составляет 22% (выражается числом 1,22 = 1: 0,82).

Каждый отрезок, направленный по осям jc, у, z или парал­лельно им, сохраняет свою величину.

Расположение осей изометрической проекции показано на рисунке 11.4. На рисунках 11.5, а, 11.6, а показаны ортого­нальные, а на рисунках 11.5, б, 11.6, б — изометрические про­екции точки А и отрезка А В.

Шестигранная призма в изометрии. Построение шестигран­ной призмы по данному чертежу в системе ортогональных про­екций (слева на рис. 11.7) приведено на рисунке 11.7. На изометрической оси z откладывают высоту Н, проводят ли­нии, параллельные осям jc и у. Отмечают на линии, парал­лельной оси jc, положение точек 1 и 4.

Для построения точки 2 определяют координаты этой точ­ки на чертеже — х₂ и у₂ — и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.

Рис. 11.6

Построение точки верхнего основания соединяют между собой, проводят ребро из точки 1 до пересечения с осью jc,

Рис. 11.7

затем — ребра из точек 2, 3, 6. Ребра нижнего основания про­водят параллельно ребрам верхнего. Построение точки А, рас­положенной на боковой грани, по координатам х_А (или у_А) и Za очевидно из рисунка 11.7.

Диметрическая проекция. Коэффициенты искажения в ди-метрической проекции выбирают следующими:

к = п; т= 1/2 к.

Тогда

2к²+ 1/4 к²; Л = л/8/9 «0,94;.

т = 0,47.

В целях упрощения построений, как и в изометрических проекциях, приведенный коэффициент искажения по осям jc

и z принимают равным 1; по оси у коэффициент искажения равен 0,5. По осям х и z или парал­лельно им все размеры откла­дывают в натуральную величину, по оси у размеры уменьшают вдвое.

Рис. 11.8

Увеличение в этом случае со­ставляет 6% (выражается числом 1,06 = 1:0,94).

Расположение осей Ох и Оу в диметрической проекции показано на рисунке 11.8. С достаточной для практических це­лей точностью оси х и у строят по тангенсам углов:

tg 7°10' = 1/8; tg 42°25'= 7/8.

Продолжение оси у за центр О_р является биссектрисой угла xO_pz, что также может быть использовано для построения оси у.

Аксонометрические изображения окружности. Окружности в аксонометрической проекции приведены на рисунке 11.9 (по­строение предложено Ю.Б. Ивановым), в диметрической —на рисунке 11.10 с указанием соответствующих значений величин осей эллипсов для приведенных коэффициентов искажения, равных 1.

Большая ось эллипсов расположена под углом 90° для эл­липсов, лежащих:

в плоскости xOz — к оси у,

в плоскости yOz — к оси х,

в плоскости хОу — к оси z-

При выполнении аксонометрического изображения от руки (как рисунка) построение эллипсов, как в изометрии, так и в диметрии, выполняют по 8 точкам. Например, по точкам 7, 2, 3, 4, 5, 6, 7 и 8 (см. рис. 11.9). Точки 1, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей эллипса.

Рис. 11.9 Рис. 11.10

При выполнении же аксонометрического изображения чер­тежным инструментом построение эллипсов в диметрической

проекции также производят по 8 точкам, а эллипсы в изомет­рической проекции можно заменять овалами и строить их сле­дующим образом. Построение показано на рисунке 11.9 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра делают засечку радиусом R = D на продолжении ма­лой оси эллипса в точке О_х (строят также аналогичным обра­зом и симметричную ей точку, которая на чертеже не показана). Из точки 0_{ как из центра проводят дугу CSC ра­диуса D, которая является одной из дуг, составляющих кон­тур эллипса. Из точки 0₂ как из центра проводят дугу радиуса 0₂S до пересечения с большой осью эллипса в точках 0₃. Проводя через точки O_h 0₃ прямую, находят в пересечении с дугой CSC точку К, которая определяет О_ъК — величину ра­диуса замыкающей дуги овала. Точки К являются также точ­ками сопряжения дуг, составляющих овал.

Аксонометрия цилиндра. Аксонометрические изображения цилиндра определяются аксонометрическими изображениями окружностей его оснований. Построение в изометрии цилиндра высотой Нпо ортогональному чертежу (рис. 11.11 слева) и точ­ки Сна его боковой поверхности показано на рисунке 11.11 справа. Пример построения в изометрической проекции круглого

У 2!\W) 3'

фланца с четырьмя цилиндрически­ми отверстиями и одним треуголь­ным приведен на рисунке 11.12. При построении осей цилиндричес­ких отверстий, а также ребер треу­гольного отверстия использованы их координаты, например координа­ты Хо И у₀.

Рис. 11.11

Аксонометрическое изображение
сферы и способ вписывания сфери­
ческих поверхностей. В прямоуголь­
ной аксонометрии поверхность
сферы проецируется на аксономет­
рическую плоскость проекций в виде
круга. Это позволяет использовать
сферу для построения аксонометри­
ческих проекций тех фигур, в кото­
рые могут быть вписаны сфери­
ческие поверхности. Так, напри-
Рис. 11.12 мер, аксонометрия поверхности

вращения в этом случае может быть построена как огибающая сфер, вписанных в эту поверхность.

Построение аксонометрических изображений деталей. По­ложение предмета в изометрической и диметрической проек­циях выбирают в зависимости от его форм и соотношения размеров. Так, детали, имеющие продолговатую (удлиненную) форму, выполняют обычно в диметрии. При этом наиболь­ший размер располагают вдоль осей х или z, по которым раз­меры не уменьшаются. В диметрии также предпочтительно выполнять детали, поверхности которых ограничены горизон­тально-проецирующими или фронтально-проецирующими плос­костями, расположенными под углом 45° к плоскости V и Н соответственно, так как эти плоскости в изометрической про­екции изображаются в виде вертикальных прямых.

Внутренние формы деталей в аксонометрических проекциях выявляют «вырезом» передней части детали.

Рациональная последовательность построения аксонометри­ческой проекции по имеющемуся эскизу или чертежу (напри­мер, рис. 11.13, а) следующая:

1) определяют вид аксонометрической проекции для изоб­ражения данного предмета — изометрия или диметрия. Деталь, показанную на рисунке 11.13, а, целесообразно изображать в диметрической проекции — рисунок 11.13, б, в, г. Выбирают достаточное место для изображения и отмечают начало коор­динат О_р;

2) проводят аксонометрические оси под установленными углами (см. рис. 11.6 и 11.8) из начала координат и строят (рис. 11.13, б) сечения предмета в плоскостях yO_pz и xO_pz. Координаты точек сечений, вьшолняемых в плоскостях yO_pz и xO_pz, берут соответственно на профильном и фронтальном раз­резах чертежа;

3) строят (рис. 11.13, в) изображение верхней части дета­ли, видимых внутренних элементов, наружные боковые по­верхности;

4) достраивают боковые элементы крепления (см. рис. 11.13, г).
Пример рациональной последовательности построения изо­
метрической проекции детали приведен на рисунке 11.14, а, б, в.

Косоугольная фронтальная диметрическая проекция. Из ко­соугольных аксонометрических проекций рассмотрим фронталь­ную диметрическую проекцию, широко используемую в учебном процессе. Положение аксонометрических осей для нее

б) \У

Рис. 11.13

Рис. 11.15 Рис. 11.16 Рис. 11.17

приведено на рисунке 11.15. Допускается применять фронталь­ные диметрические проекции с углом наклона оси у 30° и 60°. Коэффициент искажения по оси у равен 0,5, по осям х и z — 1. Окружности, лежащие в плоскостях, параллельных фрон­тальной плоскости проекций, проецируются на аксонометри­ческую плоскость проекций в окружность. Окружности, лежащие в плоскостях, параллельных горизонтальной и про­фильной плоскостям проекций, — в эллипсы (рис. 11.16). Большая ось эллипсов 2 к 3 равна 1,07, малая ось — 0,33 диа­метра окружности. Пример косоугольной фронтальной димет-рической проекции детали приведен на рисунке 11.17.

И

1. В чем заключается способ аксонометрического проецирования?

2. Что называют коэффициентами (или показателями) искажения?

3. Как производится переход от прямоугольных координат к аксоно­метрическим?

4. В каких случаях аксонометрическую проекцию называют: а) изометрической; б) диметрической; в) триметрической?

5. Чему равна сумма квадратов коэффициентов искажения для прямо­угольной аксонометрической проекции?

6. Чему равны коэффициенты искажения в прямоугольной проекции: а) изометрической; б) диметрической (при соотношении коэффи­циентов 1:0,5:1) — и каковы эти коэффициенты в приведенном (к единице) виде?

7. Как строят оси в прямоугольных проекциях:

а) изометрической; б) диметрической (1:0, 5:1)?

8. Как определяют направление и величину малой оси эллипса, явля­ющегося изометрической или диметрической проекцией окружнос­ти, расположенной в плоскостях: общего положения; фронталь­но-проецирующей и горизонтально-проецирующей; фронтальной, горизонтальной и профильной?

9. Как определить координаты точек, заданных в прямоугольной аксо­нометрической проекции, на поверхности сферы, цилиндра и ко­нуса вращения?

ЧАСТЬ ВТОРАЯ

Дата добавления: 2014-11-06