Доходы от операций с корпоративными ценными бумагами

При определении доходности корпоративных финансовых инструментов важно деление их на ценные бумаги с фиксированным либо изменяющимся уровнем дохода. Ценные бумаги с фиксированным уровнем дохода (обли­гации, привилегированные акции) обеспечивают инвестору получение заранее установленной величины дохода.

Доходность облигаций до срока погашения оценивают в зависимости от их инвестиционных качеств и текущего рыночного курса. Определение соответствующей доходности основано на применении рассмотренных ранее динамических методов, в частности метода NPV — чистой приведен­ной стоимости (капитализации дохода), в соответствии с которым стои­мость любого финансового актива представляется как современная (теку­щая) стоимость будущих платежей, поступающих от его использования. Стоимость, по которой потенциальный инвестор готов приобрести облигацию, может быть определена по формуле:

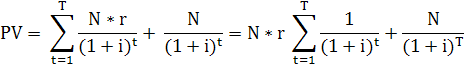
где N- номинальная стоимость облигации;

r - ставка купонного процента;

i - ставка дисконтирования, т. е. норма текущей доходности, выбираемая инвестором как наилучшая из альтернативных возможностей вложе­ния капитала;

Т- срок погашения, т. е. период, в течение которого компания должна возместить владельцу ее номинальную стоимость.

Эта формула называется основной моделью оценки облигаций (Basic Bond Valuation Model). Ее экономический смысл состоит в том, что текущая стоимость облигации равна сумме всех процентных выплат за период ее обращения и номинала, приведенных к настоящему моменту времени, т. е. дисконтированных по норме текущей доходности для дан­ного вида облигаций. При этом предполагается, что норма текущей доходности — ожидаемая инвесторами минимально необходимая вели­чина доходности по альтернативным безрисковым инвестициям и премия за риск. Отсюда текущая стоимость облигации — предписываемая ей инвестором стоимость, по которой он желал быее приобрести. Если в качестве коэффициента дисконтирования используется рыночная норма доходности, т.е. средняя из ожидаемых значений доходности отдель­ными инвесторами (это определяет соотношение спроса и предложения на данную облигацию), то текущую стоимость облигации можно рас­сматривать в качестве рыночной цены.

Пример. Пусть инвестору необходимо определить текущую стоимость облигации номиналом 1 000,0 тыс. руб., ставкой купонного дохода 30% и сроком обращения 10 лет, которая бы обеспечила ему получение 35% годового дохода (на уровне рыночной нормы доходности).

Подставляя эти величины в формулу текущей стоимости облигации, получим:

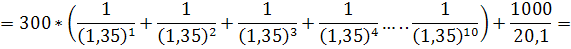
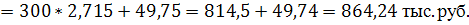
В данном случае текущая цена облигации равна 864,24 тыс. руб., что меньше ее номинала, и облигация продается с дисконтом, что то же самое. Некий совокупный инвестор готов приобрести данную облигацию только по цене ниже номинала.

Можно отметить, что, чем больше ожидаемый уро­вень дохода по облигации с позиции инвестора, т.е. рыночная норма доходности превышает установленную процентную ставку купонного дохода, тем ниже рыночная цена облигации, и наоборот. При равенстве ожидаемого уровня дохода купонной ставки рыночная цена облигации близка к номиналу.

В случае облигации с нулевым купонным доходом, т.е. без выплаты процентов в период обращения, инвестор может определить ее текущую стоимость:

PV =N/(1+i)^T,

где N — номинал облигации, руб.;

Т- период ее обращения, лет;

i - ожидаемая инвестором норма доходности, %.

Текущая стоимость облигации представляет здесь величину номина­ла, которую получит владелец при погашении облигации эмитентом и которая приведена к настоящему (текущему) моменту по ставке диско­нтирования, равной ожидаемой норме доходности. При этом ожидаемая инвестором норма доходности определяется на уровне не ниже доходности альтернативных вложений. Эта формула представляет упрощенный случай основной модели оценки облигаций.

Пример. Пусть инвестору необходимо определить текущую стоимость облигации номиналом 1 000,0 тыс. руб. и сроком обращения пять лет при условии, что ожидаемая норма доходности составит 20% годовых. Подставляя значения в формулу текущей стоимости облигации, получим:

PV =1000,0/(1 + 0,2)⁵ = 1000,0/2,49 = 402 тыс. руб.

Стоимость, равная 402 тыс. руб., представляет максимальную цену, которую инвестор захочет заплатить, или минимальную цену, по кото­рой он захочет продать, если он ожидает от инвестиций данного типа доходность в размере 20%. Такую облигацию следует купить только при цене существенно ниже номинала (с дисконтом).

Задача определения доходности от инвестирования средств в обыкновенные и привилегированные акции является более сложной, чем в облигации, поскольку существует значительная неопределенность в оценке величины будущих поступлений денежных средств по данным видам ценных бумаг.

Посравнению с позицией владельца обыкновенных акции позиция инвестора, обладающего привилегированными акциями, более благоприятна при выплате дивидендов, а также возврате первоначальной суммы инвестиций в случае ликвидации предприятия. При определении стоимости привилегированных акций единственно точно определяемым элементом служит ежегодный фиксированный дивиденд.

Величина текущей стоимости привилегированных акций представляет с позиций инвестора величину потока ожидаемых в будущем дивидендов, дисконтированных по приемлемой для него норме доходности:

PV = сумма всех выплат за инвестиционный период Д_t / (1+ i)^t, где

PV- текущая стоимость привилегированной акции, используемой неопреде­ленное число лет;

Д - величина дивидендов, планируемых к получению в t-м году;

i - норма текущей доходности.

В случае неопределенно долгого владения привилегированной акцией для определения ее текущей стоимости может использоваться следующая упрощенная формула:

PV = (N*r)/ i.

Рассчитанная таким образом величина определит цену, которую ин­вестор пожелает заплатить за привилегированную акцию, или минималь­ную цену, за которую он согласится продать акцию. Как правило, ни один инвестор не планирует держать у себя бесконечно долгое время конкретную ценную бумагу, поскольку возникают возможности для более выгодного использования средств. Если инвестор может надеяться продать акцию по определенной цене в известное время, то норму доходности такой акции можно определить:

i =(N*r)/PV.

Инвестирование средств в обыкновенные акции должно обеспечить ожидаемый в будущем поток движения наличности, состоящий из вели­чины предполагаемых в каждом году дивидендов и цены, которую инвесторы надеются получить при продаже акции в конце некоторого периода и которая включает прибыль от первоначального инвестирова­ния и доход с прироста капитала (либо потери капитала). Планируемый период владения акциями у различных инвесторов может сильно раз­личаться. Те из них, которые хранят их долго, ожидают будущие ди­виденды и возможность продать акции по цене выше той, которую они заплатили. Эта конечная стоимость будет зависеть от желания в этот момент других инвесторов купить предложенные акции. Цена, которую они готовы заплатить, в свою очередь, будет зависеть от ожиданий дивидендного дохода и конечной стоимости.

Общая величина дохода всей цепи инвесторов, вкладывающих свои средства в акции, представляет сумму распределений со стороны ко­мпании наличных средств — будь то наличные дивиденды, ликвида­ционные дивиденды или выплаты в процессе выкупа акций, т.е. любое распределение денежных средств акционерам, включая выкупы акций. Акционеры ожидают, что, реинвестируя получаемую прибыль, компания увеличивает будущую прибыльность их вложений и предельный размер дивидендов.

Если инвестор предполагает держать акцию один год и цена акции будет расти при ставке g, то текущая стоимость такой акции будет:

PV =(Д+ PV(1+g))/(1+i),

где Д-ожидаемый в конце года дивиденд;

g - темп роста курса акции в течение года, %;

i- ставка дисконтирования.

Отсюда:

PV =Д/ i - g.

Данное выражение представляет собой текущую стоимость ожидаемых дивидендов и цену акции в конце года, дисконтированную при соответствующей норме прибыли i. Если фактическая цена акции выше PV, то инвестор не купит ее, либо, если владеет акцией, продаст ее.

Так, например, если в прошлом году компания выплатила на акцию 10,0 тыс. руб. дивидендов, причем прибыли компании и соответственно дивиденды росли в среднем на 5% ежегодно за ряд лет, то инвестор, предполагая, что темп роста сохранится и цена акции также возрастет на 5%, может определить ожидаемую величину дивиденда:

Д₁ = Д(1 +g) = 10,0*1,05 = 10,5 тыс. руб.

Если предположить, что норма прибыли по аналогичным акциям равна 12%, то можно определить ее текущую стоимость:

PV =10,5 /(0,12 — 0,05) =150,0 тыс. руб.

где Д₁ - ожидаемые дивиденды в конце периода t;

PV — ожидаемая стоимость акции в конце периода Т.

Дата добавления: 2014-11-08