
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 12. Теплопередача
|
|
|
|
Радиационно-конвективный теплообмен и теплопередача. Сочетание простых процессов теплопроводности, теплоотдачи и излучения образует сложные процессы. Эти процессы могут протекать последовательно или параллельно.
Сложный вид переноса тепла при параллельном и одновременном протекании процессов теплоотдачи и излучения называют радиационно-конвективным теплообменом.
Сложный вид переноса тепла от одной среды к другой через разделяющую твердую стенку называют теплопередачей. При теплопередаче последовательно протекают процессы теплоотдачи и теплопроводности.
Результат сложного процесса переноса теплоты, как правило, приписывается одному, главному из простых процессов - конвекции, излучению или теплопроводности. Влияние остальных составляющих учитывается количественно соответствующими коэффициентами пропорциональности.
Суммарный коэффициент теплоотдачи. Если главной в процессе является теплоотдача, то плотность теплового потока при совместном действии теплоотдачи и излучения будет:
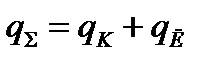
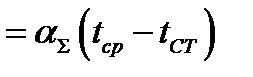 ,
,
где 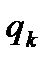 и
и 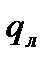 - поток теплоты теплоотдачей и излучением;
- поток теплоты теплоотдачей и излучением;
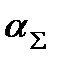 - суммарный (общий) коэффициент теплоотдачи. Найдем
- суммарный (общий) коэффициент теплоотдачи. Найдем 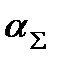 :
:
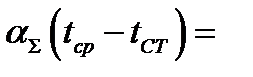
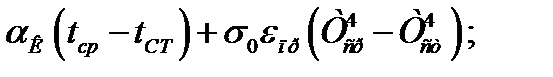
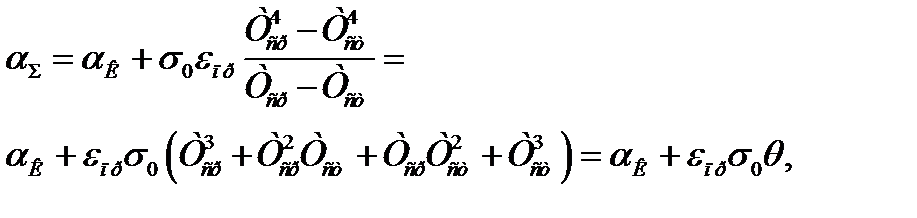
где 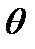 - температурный коэффициент.
- температурный коэффициент.
Т.о., суммарный коэффициент теплоотдачи:
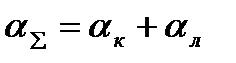 ,
,
где 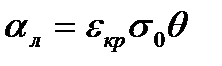 - коэффициент теплоотдачи излучением.
- коэффициент теплоотдачи излучением.
Если главным является излучение, то суммарная теплоотдача может быть определена следующим образом:
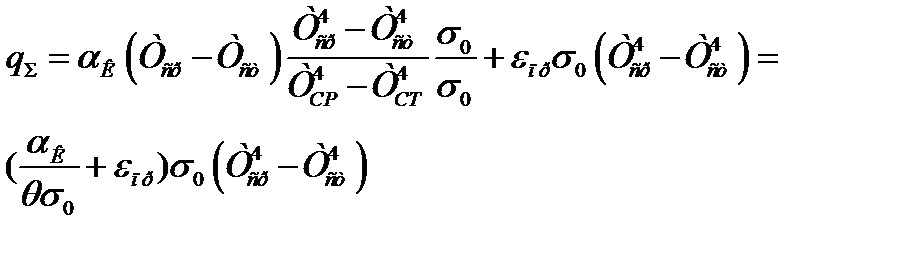
или 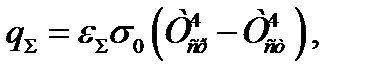
где 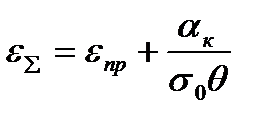 - суммарная степень черноты.
- суммарная степень черноты.
Теплопередача через плоскую стенку. Коэффициент и термическое сопротивление теплопередачи. Как уже отмечалось, теплопередача – это перенос теплоты от одной среды к другой через разделяющую стенку. Определим удельный тепловой поток через плоскую однородную стенку толщиной d от одной среды (жидкости или газа) с температурой 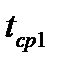 к другой с температурой
к другой с температурой 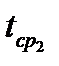 . Коэффициенты теплоотдачи α1, α2, а также коэффициент теплопроводности λ постоянны.
. Коэффициенты теплоотдачи α1, α2, а также коэффициент теплопроводности λ постоянны.
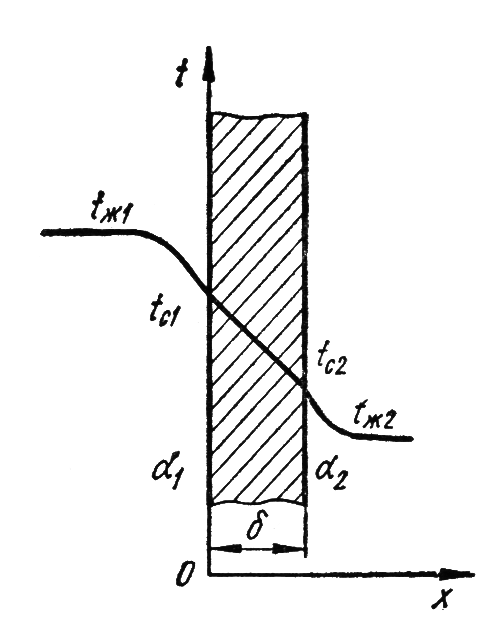
| Рис.12.1. Теплопередача через плоскую стенку |
При установившемся состоянии количество теплоты, переданное от горячей среды к стенке, равно количеству теплоты, прошедшему в стенке, и количеству теплоты, отданному от стенки к холодной среде. Т.е., для плотности теплового потока справедливы выражения:
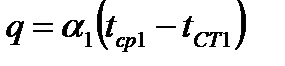 ;
;
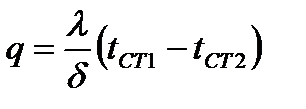 ;
;
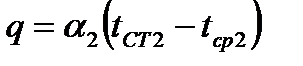 .
.
Из этих уравнений найдем частные температурные напоры:
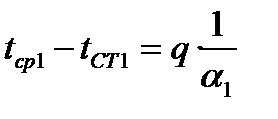 ;
;
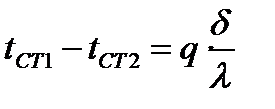 ;
;
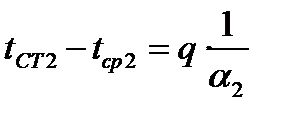 .
.
Складывая их, получим полный температурный напор:
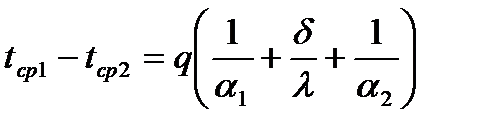 .
.
Тогда плотность теплового потока:
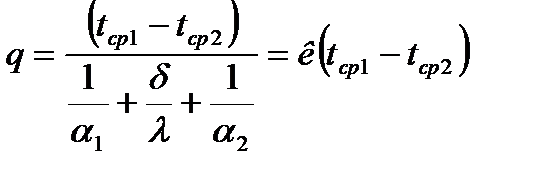 ,
,
где 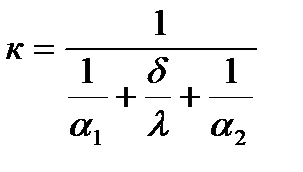 - коэффициент теплопередачи.
- коэффициент теплопередачи.
Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из полученного уравнения следует, что эта величина равна:
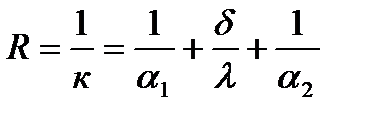 -
-
Т.е., общее термическое сопротивление равно сумме частных сопротивлений:
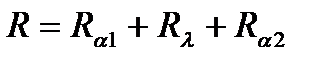 ,
,
где 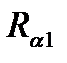 =1 /a1 – частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя;
=1 /a1 – частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя;
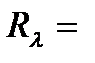 d/l - частное термическое сопротивление теплопроводности (стенки);
d/l - частное термическое сопротивление теплопроводности (стенки);
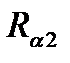 =1 /a2 – частное термическое сопротивление со стороны холодного теплоносителя.
=1 /a2 – частное термическое сопротивление со стороны холодного теплоносителя.
Общее количество тепла, переданное через стенку площадью 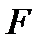 , составит:
, составит: 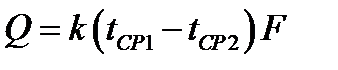 . Это основное уравнение теплопередачи.
. Это основное уравнение теплопередачи.
Из уравнений для частных температурных напоров найдем температуру поверхностей стенки:
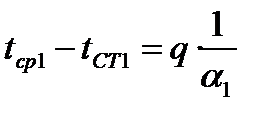 →
→ 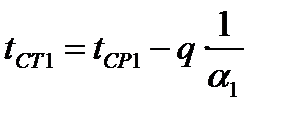
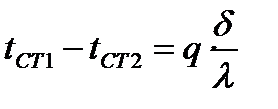 →
→ 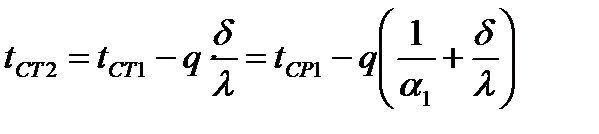
Данное решение соответствует граничным условиям III-го рода, т.к. заданы температуры среды tср1, tср2 и коэффициенты теплоотдачи α1, α2.
Для многослойных стенок выражения, из которых определяются плотность теплового потока и коэффициент теплопередачи, имеют вид:
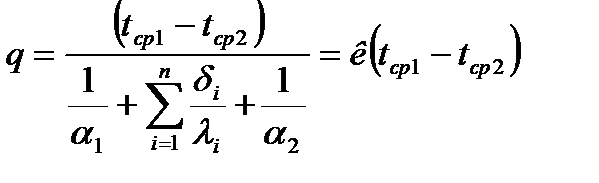 ;
; 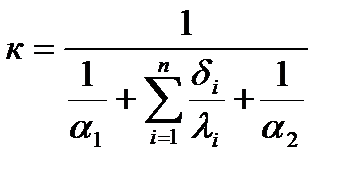 .
.
Температура поверхности за любым (к – тым) слоем:
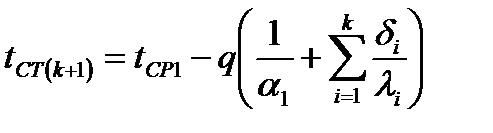 .
.
Пути интенсификации теплопередачи. Из основного уравнения теплопередачи 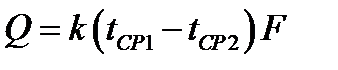 видно, что при заданных температурах подвижной среды t СР1 и t СР2процесс определяют коэффициент k и площадь поверхности теплообмена F. Для плоской стенки коэффициент теплопередачи:
видно, что при заданных температурах подвижной среды t СР1 и t СР2процесс определяют коэффициент k и площадь поверхности теплообмена F. Для плоской стенки коэффициент теплопередачи:
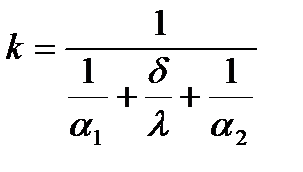 .
.
Слагаемые в знаменателе - это термические сопротивления на пути переноса теплоты. Снижение каждого из них интенсифицирует теплопередачу. Обычно термическое сопротивление теплопроводности 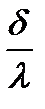 незначительно по сравнению с величинами
незначительно по сравнению с величинами 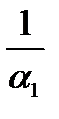 и
и 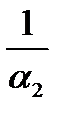 . Это обусловлено высокими значениями l и небольшой толщиной стенки. Поэтому
. Это обусловлено высокими значениями l и небольшой толщиной стенки. Поэтому 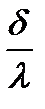 можно пренебречь и записать:
можно пренебречь и записать:
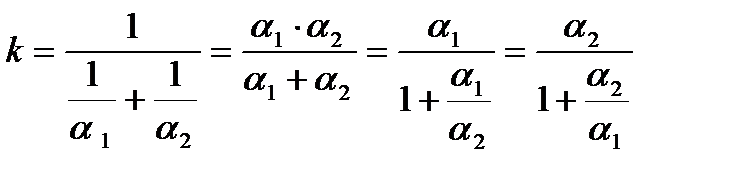 .
.
Если 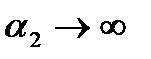 , то
, то 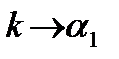 ; если
; если 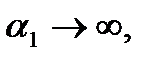 то
то 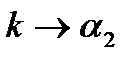 . Таким образом, коэффициент теплопередачи k не может быть больше самого малого значения a. Например, при
. Таким образом, коэффициент теплопередачи k не может быть больше самого малого значения a. Например, при 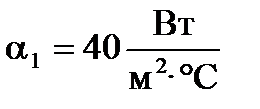 и
и 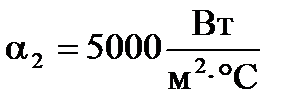 величина коэффициента теплопередачи составит
величина коэффициента теплопередачи составит 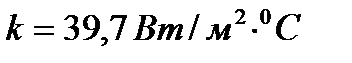 ; при
; при 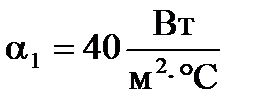 и
и 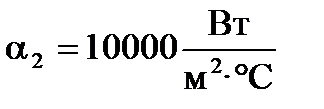 -
- 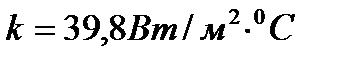 .
.
Если 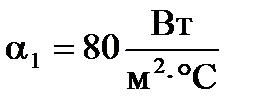 и
и 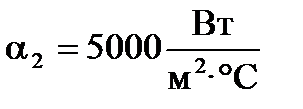 , то
, то 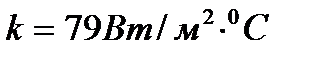 ; если
; если
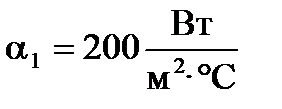 и
и 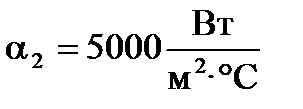 , то
, то 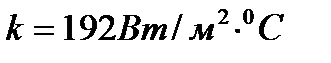
Из этих примеров видно, что при 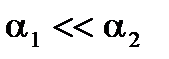 увеличение большего из коэффициентов теплоотдачи (
увеличение большего из коэффициентов теплоотдачи (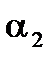 ) практически не увеличивает коэффициент k. Увеличение меньшего из коэффициентов теплоотдачи (a1) в 2,5 раза дает увеличение коэффициента k почти во столько же раз. Таким образом, для существенной интенсификации теплопередачи следует увеличивать меньший из коэффициентов теплоотдачи.
) практически не увеличивает коэффициент k. Увеличение меньшего из коэффициентов теплоотдачи (a1) в 2,5 раза дает увеличение коэффициента k почти во столько же раз. Таким образом, для существенной интенсификации теплопередачи следует увеличивать меньший из коэффициентов теплоотдачи.
Вторым направлением интенсификации теплопередачи является оребрение стенок. Тепловой поток через стенку любой формы можно рассчитать по формуле:
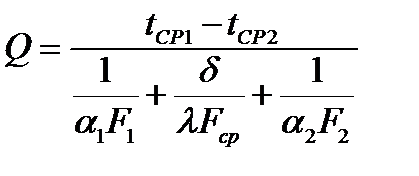 ,
,
где 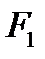 ,
, 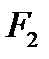 ,
, 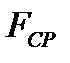 - площадь теплообмена со стороны горячего теплоносителя, со стороны холодного и площадь стенки по ее середине.
- площадь теплообмена со стороны горячего теплоносителя, со стороны холодного и площадь стенки по ее середине.
Отсюда видно, что термические сопротивления 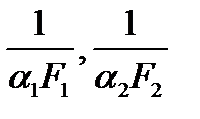 можно уменьшить путем увеличения поверхностей F1 или F2, например, за счет их оребрения.
можно уменьшить путем увеличения поверхностей F1 или F2, например, за счет их оребрения.
Теплопередача через цилиндрическую стенку. Однородная цилиндрическая стенка с внутренним диаметром d1 и наружным d2 имеет постоянный коэффициент теплопроводности λ. Граничные условия III-го рода заданы постоянными температурами среды tср1, tср2 и постоянными коэффициентами теплоотдачи на поверхностях стенки α1, α2. Длина трубы велика по сравнению с толщиной стенки, поэтому потерями теплоты с торцов можно пренебречь. Найдем линейную плотность теплового потока и температуры поверхностей стенки.
В стационарном режиме количество тепла, передаваемой от горячей среды к стенке, проходящей через стенку и отдаваемой стенкой к холодной среде, одинаково, т.е.:
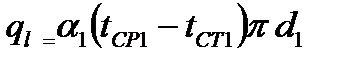 →
→ 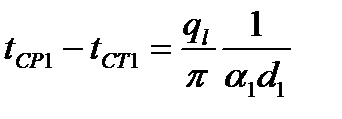
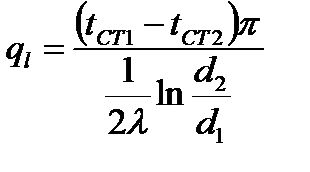 →
→ 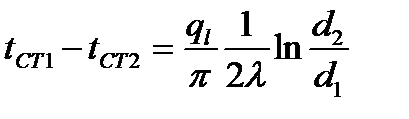
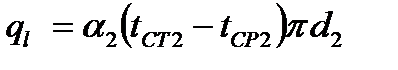 →
→ 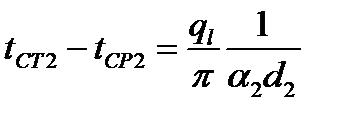
Суммируя правые и левые части последних уравнений, получим выражение для определения линейной плотности теплового потока:
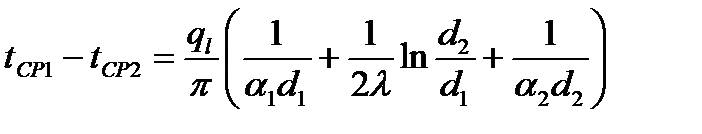 → →
→ → 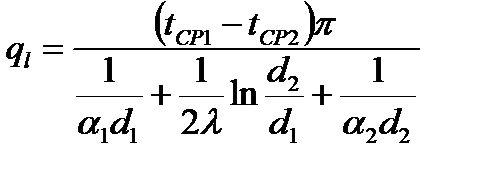
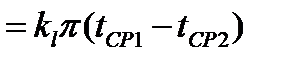 , Вт/м∙град,
, Вт/м∙град,
где 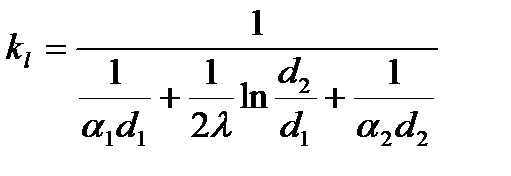 - линейный коэффициент теплопередачи; он показывает количество теплоты, проходящее через стенку длиной в один метр в единицу времени от одной среды к другой при разности температур между ними в один градус.
- линейный коэффициент теплопередачи; он показывает количество теплоты, проходящее через стенку длиной в один метр в единицу времени от одной среды к другой при разности температур между ними в один градус.
Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи:
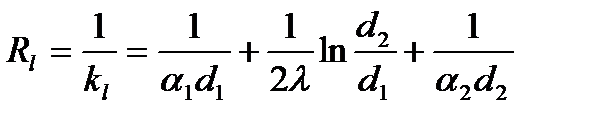 ,
,
где 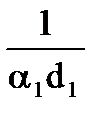 ,
, 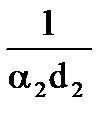 ,
, 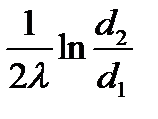 - частные термические сопротивления теплоотдачи на внутренней и внешней поверхности и теплопроводности стенки.
- частные термические сопротивления теплоотдачи на внутренней и внешней поверхности и теплопроводности стенки.
Из тех же уравнений для разностей температур найдем температуры внутренней и внешней поверхности стенки:
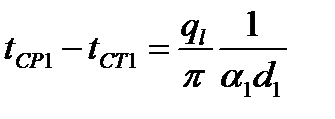 →
→ 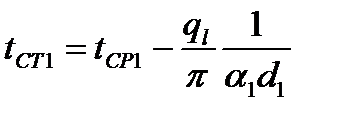 ;
;
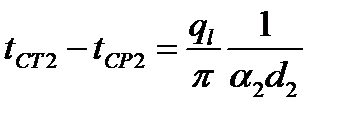 →
→ 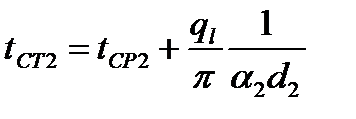 или
или
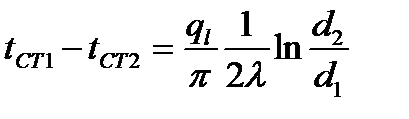 →
→ 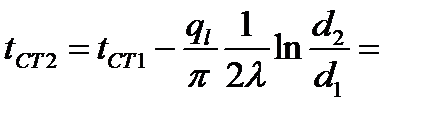
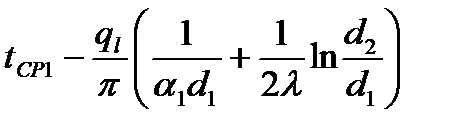
Для стенки из n слоев плотность линейного теплового потока и температура за к – тым слоем:
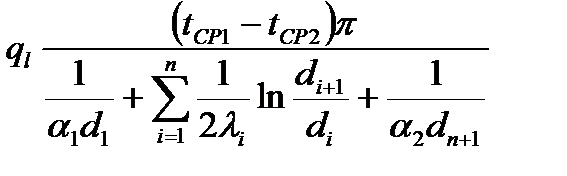 ;
; 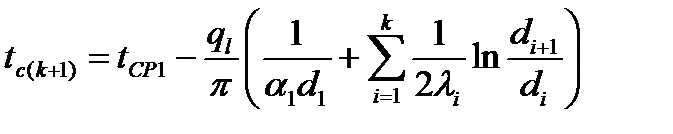 .
.
Критический диаметр цилиндрической стенки. Из уравнения для линейного термического сопротивления теплопередачи однослойной стенки:
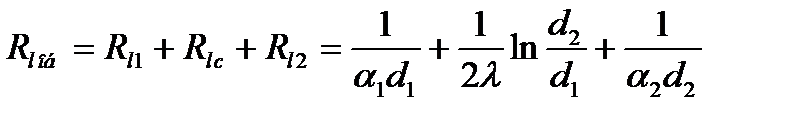
видно, что наружный диаметр d2 одновременно увеличивает термическое сопротивление теплопроводности стенки 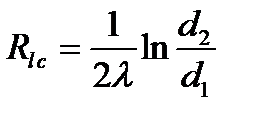 и уменьшает термическое сопротивление теплоотдачи
и уменьшает термическое сопротивление теплоотдачи 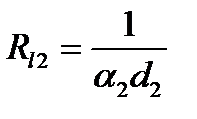 (рис. 12.2).
(рис. 12.2).
Рис. 12.2. Зависимость термического сопротивления
цилиндрической стенки от диаметра d2
Исследуем это уравнение на экстремум по переменной d2, взяв производную и приравняв ее нулю:
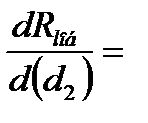
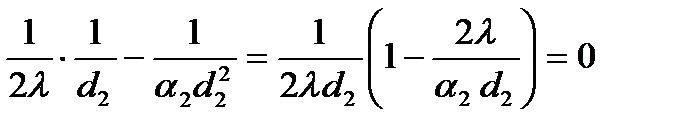 →
→ 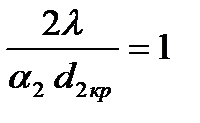 →
→ 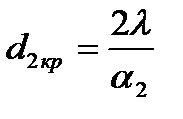
Можно показать, что вторая производная этого уравнения больше нуля, что свидетельствует о наличии минимума функции.
Диаметр трубы, соответствующий минимуму суммарного термического сопротивления, называется критическим. При этом плотность теплового потока максимальна. При 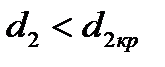 с увеличением d2 тепловой поток возрастает. Это обусловлено преобладающим влиянием на него роста наружной поверхности трубы. При
с увеличением d2 тепловой поток возрастает. Это обусловлено преобладающим влиянием на него роста наружной поверхности трубы. При 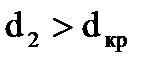 с ростом наружного диаметра тепловой поток уменьшаться. Здесь преобладает влияние роста термического сопротивления теплопроводности стенки.
с ростом наружного диаметра тепловой поток уменьшаться. Здесь преобладает влияние роста термического сопротивления теплопроводности стенки.
Тепловая изоляция. Чтобы уменьшить потери тепла в окружающую среду, трубы с горячим теплоносителем покрывают изоляцией. Но изоляция в определенных условиях может привести, как это не парадоксально, и к обратному результату – увеличению тепловых потерь.
Термическое сопротивление трубы с изоляцией, коэффициент теплопроводности которой λиз, наружный диаметр dиз, составляет:
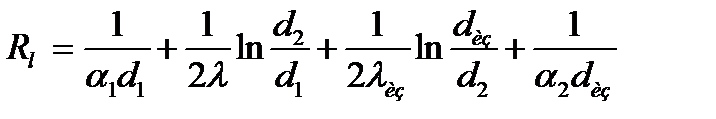 .
.
Выполнив исследования этого выражения на экстремум по dиз, аналогичные приведенным выше, получим критический диаметр изоляции, при котором наблюдается минимум суммарного термического сопротивления Rl и, соответственно, максимум тепловых потерь (рис. 12.3):
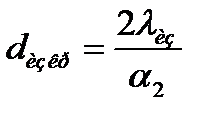 .
.
Рис. 12.3. Зависимость тепловых потерь от толщины изоляции
цилиндрической стенки
При dиз = d2 изоляция отсутствует. С увеличением dиз от d2 до dизкр тепловые потери возрастают; по достижении dиз= dизкр они максимальны, а с дальнейшим увеличением dиз потери тепла постепенно снижаются. Они снова достигают того же значения, что и без изоляции, лишь при некотором значении d3эф. Очевидно, что применять изоляцию с диаметром, меньшим d3эф нет смысла, т.к. потери тепла при этом будут больше, чем без нее.
Теплопередача через сферическую стенку. При граничных условиях III - го рода, кроме внутреннего r1 и внешнего радиуса сферы r2, заданы температуры среды внутри и снаружи tср1 и tср2, а также коэффициенты теплоотдачи на поверхностях стенки α1 и α2.
Для стационарного процесса тепловой поток Q постоянный для всех изотермических поверхностей:
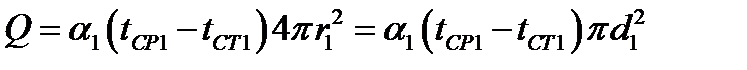
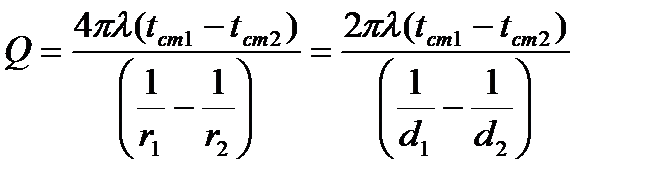
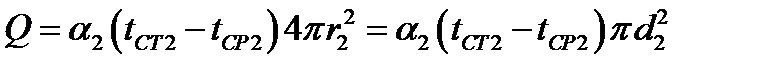
Из этих уравнений находим:
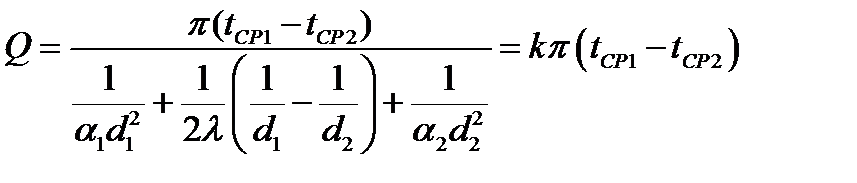 ,
,
где  - коэффициент теплопередачи сферической стенки.
- коэффициент теплопередачи сферической стенки.
Обобщенный метод решения задач теплопередачи для тел произвольной формы. Уравнение теплового потока теплопередачи для пластины можно представить в виде:
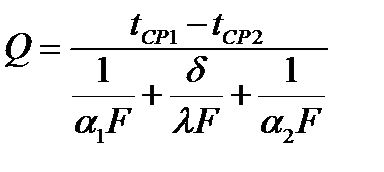 .
.
Для цилиндра выражение для расчета теплового потока может быть представлено в виде
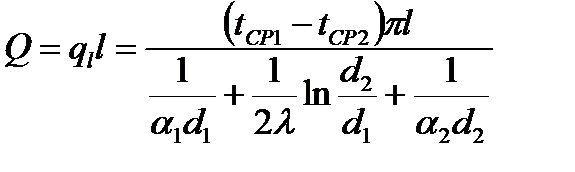
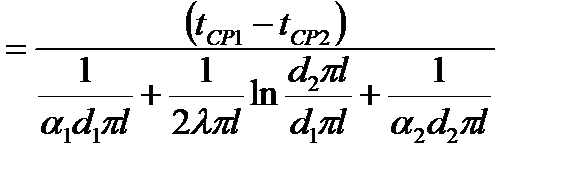 ,
,
где d 1 πl = F1 - внутренняя поверхность цилиндра;
d2πl = F2 – его наружная поверхность.
Выполним логарифмическое усреднение поверхностей F1 и F2:
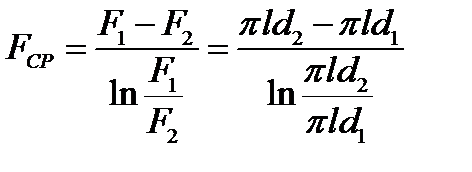 .
.
Тогда уравнение теплопередачи для цилиндра примет вид:
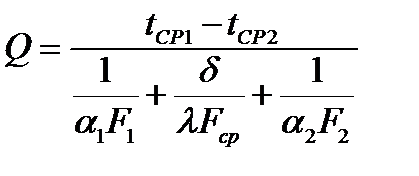 .
.
Для сферической стенки тепловой поток может быть определен по этому же уравнению, если средней поверхность сферы найти геометрическим усреднением поверхностей:
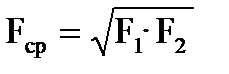 .
.
Таким образом, для стенок классической формы (пластина, цилиндр, сфера), а также для тел произвольной формы расчет теплового потока может производиться по единой формуле:
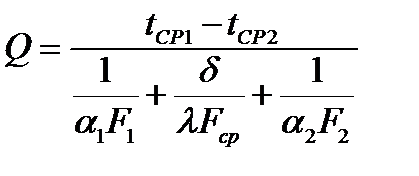 ,
,
учитывая, что для пластины 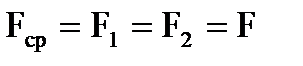 , для цилиндра
, для цилиндра 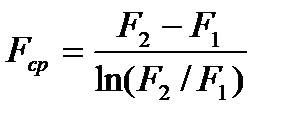 , для сферы
, для сферы 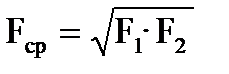 . Для тел произвольной формы среднею поверхность рассчитывают по формуле усреднения, наиболее приближенной к одной из классических форм.
. Для тел произвольной формы среднею поверхность рассчитывают по формуле усреднения, наиболее приближенной к одной из классических форм.
Для стенки из n слоев тепловой поток и температура за к – том слоем:
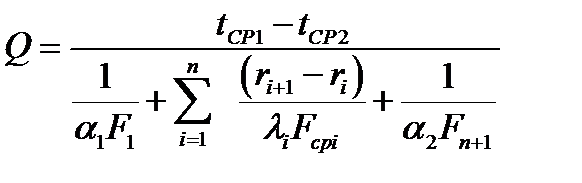 ;
;
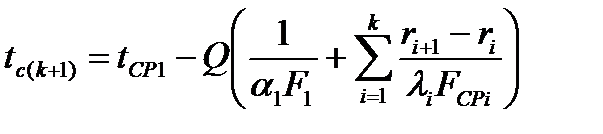 .
.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 2090; Нарушение авторских прав?; Мы поможем в написании вашей работы!