Принципы логического вывода

Вопросы

1. Что такое дизъюнкция?

2. Что такое конъюнкция?

3. Когда истинно отрицание?

4. Когда ложно отрицание?

5. Когда истинна конъюнкция?

6. Когда истинна дизъюнкция?

7. Чему соответствует отрицание отрицания?

8. Чему соответствует отрицание конъюнкции?

9. Чему соответствует отрицание дизъюнкции?

Задания

1. Проверьте запросы с отрицаниями в Интернет и объясните полученные результаты:

запрос: «-(-интернет)»

запрос: «поиск -интернет»

запрос: «поиск информации -интернет»

запрос: «информатика -Ершов»

2. Составьте таблицы истинности для утверждений:

а)(не А) и (не В);

б)(не А) или (не В);

в) А и (не В);

г) А или (не В).

3. Сравните с помощью таблиц истинности логические выражения:

а) не (А и В) и(не А) или (не В);

б) не (А и В) и(не А) или (не В);

в) не (А) и В и А и (не В);

г) не (А) или В и А или (не В).

4. Проверьте по таблицам истинности логические законы:

а) отрицание конъюнкции:

не (А и В) ≡(не А) или (не В);

б) отрицание дизъюнкции:

не (А или В)≡(не А) и (не В);

в) отрицание отрицания:

не (не А) ≡ А;

г) отрицание двойного отрицания:

не (не (не А)) ≡(не А).

Могут ли компьютеры думать? — одна из самых интригующих проблем информатики как науки была сформулирована английским математиком А. Тьюрингом при появлении самых первых компьютеров.

Ответ А. Тьюринга — да, если удастся создать такие диалоговые программы, которые смогут отвечать на вопросы так же, как и люди. В настоящее время такого типа диалоговые программы получили название — экспертные системы.

Создание «искусственного интеллекта» стало целью огромного потока научных работ и исследований, вылившихся в создание программ для ЭВМ, имитирующих интеллектуальную деятельность людей — игру в шахматы, шашки, решение задач и доказательство теорем.

Первые шахматные программы и первые универсальные решатели задач были созданы еще для самых первых громоздких ЭВМ. В это же время были заложены основные принципы создания систем искусственного интеллекта, основанные на логическом выводе решения самых разнообразных интеллектуальных задач.

К концу XX в. программы, которые могут играть в шахматы наравне с людьми, появились и тиражируются для персональных компьютеров, а программистам фирмы IBM удалось для своего очередного суперкомпьютера создать шахматную программу, которая смогла обыграть Г. Каспарова — чемпиона мира по шахматам.

Все программы для ЭВМ, демонстрирующие интеллектуальное поведение, созданы и работают строго в соответствии с законами и принципами математической логики. Без понимания этих законов невозможно понимание принципов работы и развития вычислительных машин вообще и исследований в области искусственного интеллекта в частности.

Фундаментом вычислительных наук является конструктивная математика, в основе которой лежит математическая логика и теория алгоритмов. Математическая логика с самого начала использовалась для описания элементов и узлов ЭВМ, а теория алгоритмов — для изучения свойств компьютерных программ.

Основными объектами в математической логике являются высказывания и предикаты. Первые изучаются в исчислении высказываний, а вторые — в исчислении предикатов.

Высказывания — это суждения, которые могут быть истиными или ложными. Исчисление высказываний изучает свойства сложно-составных суждений и не интересуется, что утверждается в этих суждениях.

Высказывания обычно обозначаются отдельными буквами или буквами с возможными индексами. Примеры простых высказываний и их обозначений:

А = «снег белый»;

В₁= «вода теплая»;

В₂ = «земля твердая».

С математической точки зрения высказывания — это переменные, принимающие значения «истина» («true») или «ложь» («false»). Эти два истинностных значения иногда заменяются словами «да» («yes»), «нет» («not») либо цифрами 1 и 0.

Предикаты — это суждения о некоторых переменных объектах или их свойствах. Примеры предикатов:

А(х) = «цвет = х»;

В(х, у) = «х < у»,

где х, у — это некоторые переменные (объекты).

Значениями переменных в предикатах могут быть числа, слова, векторы, списки, функции, процедуры, алгоритмы, программы, более точно — конструктивные объекты. Для математической логики существенно, чтобы эти объекты имели конструктивную форму и были бы строго определены.

Примеры обозначения предикатов с конкретными значениями:

А (красный) = «цвет = красный»;

В (рост, 180) = «рост < 180»;

В (рост, у) = «рост < у».

Из приведенных примеров предикатов и высказываний понятно, что семантика языков запросов в Интернет описывается законами исчисления высказываний, а семантика языков запросов к базам данных на ЭВМ — законами исчисления предикатов (с равенствами).

Истинность сложных высказываний и предикатов может исследоваться через анализ их всевозможных интерпретаций либо путем их доказательства или опровержения. Так для опровержения любого общего утверждения достаточно указать хотя бы один контрпример.

Исчерпывающий анализ сложных высказываний проводится с помощью таблиц истинности, рассмотренных в предыдущем разделе. Высказывание — общезначимо (тождественно истинно), если оно истинно при любых значениях входящих в него суждений.

Доказательство — это последовательность суждений, обосновывающих некоторое утверждение. Собственно доказательства строятся на основе некоторых правил вывода, в которых одни утверждения являются (пред)посылками, а другие — их следствиями.

На практике исходным для доказательства утверждений являются некоторые факты и аргументы. В математике доказательства опираются на аксиомы, принятые в рассматриваемой теории, истинность которых не обсуждается.

Важнейшей операцией математической логики, на которой построены основные математические исследования теорий и доказательства теорем, является импликация, имеющая обозначение А → В.

Импликация А → В — это логическое следование. Импликация А → В читается: «если А, то В», «из А следует В», «А влечет В» и т. п. Первое суждение в импликации называется посылкой, а второе — следствием.

Примеры правил логического вывода:

а) над высказываниями:

если «на улице дождь», то «на улице мокро»;

б) над предикатами:

любит (х, конфеты) → сластена (х).

Таблица истинности импликации:

Свойства импликации:

П1: «Импликация А → В ложна,

когда посылка А истинна, а следствиеВ — ложно».

П2: «Импликация А → В истинна,

когда истинно следствие либо ложны и посылка и следствие».

Общий закон логического вывода был указан Аристотелем — основателем логики как научной дисциплины — и назван modus ponens:

Примеры логического вывода:

Аристотелем данная формулировка закона логического вывода была дана на языке исчисления высказываний. В таком виде она содержится во всех учебниках по логике и учебниках по математической логике.

В исчислении предикатов этот закон сохраняет свою силу. Однако в предикатной форме закон логического вывода превращается в конструктивную процедуру вывода новых сведений из имеющихся конкретных фактов и правил вывода.

Первый принцип логического вывода:

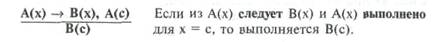
Данная процедура вывода позволяет вывести суждение В(с) из конкретного факта А(с) и правила А(х) → В(х). Пример логического вывода:

Таким образом, данное конструктивное правило позволяет выводить новые сведения из общих правил и уже известных фактов. Следовательно, знание фактических сведений и применение законов логического вывода позволяет порождать новые сведения, являющиеся их следствиями.

Этим свойством и этими законами логического вывода могут пользоваться не только люди — они применяются в механизмах автоматического доказательства теорем, заложенных в современных системах искусственного интеллекта.

Принцип вывода отрицаний — второй общий принцип логического вывода:

Данная процедура из отрицания следствия не В(с) на основании правила вывода А(х) → В(х) позволяет сделать заключение о невыполнении предпосылки не А(с). Примеры логического вывода из отрицаний:

Данный принцип также представляет конструктивную процедуру вывода новых сведений — отрицаний предросылок не А(с) при нарушении следствий не В(с) для заданного правила А(х) → В(х).

Приведенные принципы и законы логического вывода и заложены в современные модели систем искусственного интеллекта. В частности, они заложены в механизмы системы логического программирования Пролог, который в 90-х годах был принят японским правительством в основу проекта нового поколения ЭВМ.

Дата добавления: 2014-11-25