Решение задач на ЭВМ

Вопросы

1. Что такое исходные и результирующие данные?

2. Что такое входные, выходные и сохраняемые данные?

3. Что такое представление данных?

4. Как описываются массивы в программах на Бейсике?

5. Какие типы переменных есть в программах на Бейсике?

6. Как описываются данные в программах на Бейсике?

Задания

1. Составьте сценарий, алгоритм и программу поиска номера телефона по фамилии с представлением сведений в последовательности операторов data.

2. Составьте сценарий, алгоритм и программу поиска по имени дней рождения родных: мамы, папы, сестер и братьев, используя операторы data.

3. Составьте сценарий, алгоритм и программу поиска следующих данных о друзьях, используя операторы data для получения сведений:

а) о росте друзей;

б) о весе друзей;

в) о цвете глаз.

4. Составьте сценарий, алгоритм и программу поиска сведений о расписании занятий по дням недели, используя операторы data.

5. Составьте сценарий, алгоритм и программу поиска сведений о расписании занятий, используя операторы data:

а) по названию предмета;

б) по дням недели;

в) по номеру урока.

6. Составьте алгоритм и программу построения изображения ломаной по координатам точек, записанных в последовательности операторов data.

7. Составьте алгоритм и программу вывода изображений ткани из цветных кругов по данным об их центрах и радиусах, записанных в последовательности операторов data.

Глава 5. ТЕХНОЛОГИЯ РЕШЕНИЯ ЗАДАЧ

Решение задач должно начинаться с их точной постановки. Постановка задач — это четкое выделение того, что требуется, и того, что дано:

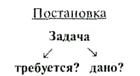
Следующий этап — определение способа решения задачи. Способ решения — это набор действий, позволяющих получить требуемое из исходного:

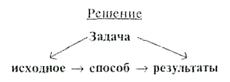
Результат правильный, если он отвечает требованиям. Получение результатов — главное в решении любых задач. Отсутствие или неправильность результатов говорит о неуспехе деятельности.

Результат неправильный, если он не соответствует требованиям. Однако при отсутствии четких требований невозможно однозначно судить о правильности или неправильности результатов.

При решении на ЭВМ постановка задач предполагает представление требуемого и исходного в виде данных. Способы решения задач на ЭВМ в такой постановке должны быть представлены соответствующими алгоритмами и программами обработки данных.

При отсутствии готовых программ для решения задач возникает проблема создания соответствующих алгоритмов и программ. В любом случае необходимо подобрать и определить способы, методы и средства для решения поставленных задач.

Систематический подход к составлению программ предполагает в качестве первого этапа составление спецификаций — описаний форм ввода и хранения данных в ЭВМ, а также получения и вывода результатов. Эти спецификации в дальнейшем будут использоваться для оценки правильности созданных программ.

Для диалоговых программ в роли таких спецификаций выступают сценарии диалога — полные описания результатов и правил работы с ЭВМ при решении поставленных задач. Только после создания таких спецификаций должны составляться соответствующие им алгоритмы и программы.

Приведенная схема представляет основной принцип систематических методов составления алгоритмов и программ для решения различных прикладных задач — экономических, математических, физических, инженерных и т. д.

Особенностью систематических методов является возможность полного устранения ошибок из алгоритмов и программ. При этом подходе программы сверяются с описаниями алгоритмов, а алгоритмы — с описаниями сценариев и методов решения.

Такой систематический подход к составлению алгоритмов и программ может применяться к решению на ЭВМ любых прикладных задач с использованием самых различных языков программирования — Бейсик, Паскаль, Си и им подобные. Приведем примеры систематического решения задач.

Первая задача: подсчет площади треугольника по длинам сторон.

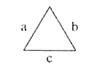
Постановка

Дано: а, b, с — длины сторон.

Треб.: S — площадь треугольника.

При: a > 0, b > 0, с > 0,

a < b + c, b < a + c, c < a + b.

Метод решения

Обратите внимание: в постановке задачи в исходные условия включены ситуации, когда решение может не существовать. А именно, здесь указаны три неравенства треугольника и условия положительности длин сторон. При нарушении этих условий треугольника просто не существует и тем более нельзя говорить о его площади.

Для надежности программ такого рода ситуации (когда нет решений) должны быть предусмотрены в сценарии диалога. В этих случаях в сценарий необходимо включить сообщения с диагностикой причин отказов: отсутствие решений, недопустимость данных, некорректность команд, противоречивость фактов и т. п.

АлгоритмПрограмма

алг «площадь треугольника» ' площадь треугольника

нач сls

вывод («площадь треугольника»)? «площадь треугольника»

вывод («длины сторон:»)? «длины сторон:»

запрос («а=», a) input «a=»,a

запрос («b=», b) input «b=»,b

запрос («с=», с) input «c=»,c

если не (а > 0 и b > 0 и с > 0) то if a<=0 or b<=0 or c<=0 then

вывод («недопустимы длины»)? «недопустимы длины»

инес не (а < b + с и b < а + c elseif not (a < b + с and b < а + с

и с < а + b) то and с < а + b) then

вывод («недопустимы длины»)? «недопустимы длины»

иначе else

р:= (а + b + с)/2 р = (а+b+с)/2

S:= 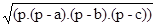S = sqr (p*(p-a)*(p-b)*(p-c))

вывод («площадь=», S)? «площадь=», S

все end if

кон end

Рассмотренный пример служит иллюстрацией постановки задачи, в которой выделены как требуемые и исходные данные, так и условия допустимости исходных данных. Такая постановка задачи позволяет заранее выделить все случаи и ситуации недопустимости данных, что в дальнейшем понадобится при составлении сценария диалога с компьютером.

В общем случае математическая постановка задач должна содержать не только условия допустимости данных, но и точное описание требований к результатам:

1) дано: перечень исходных данных;

2) треб.: перечень требуемых данных;

3) где: требования к результатам;

4) при: условия допустимости данных.

Вторая задача: определение среднего арифметического последо­вательности из N чисел х₁, х₂,..., х_N. Приведем постановку, метод решения и сценарий диалога для решения этой задачи.

Постановка задачиСценарий

Дано: N - количество чисел, среднее N чисел

x₁, х₂,.., х_N - числа, чисел =? <N>

Треб.: s - среднее N чисел. *

Где: s = (х₁, + х₂ +...+ х_N)/ N. 1: <х₁>

При: N > 0. 2: <х₂>

………..

Метод решения N: <х_N>

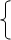S₀ = 0 среднее = <s>

S_k = S_k-1 + х_k

[k = 1,..., N] недопустимо N

s = S_N / N

Обратите внимание: метод вычисления среднего N чисел здесь описан через подсчет суммы чисел. Правильность метода может быть проверена по отношению к требованиям постановки задачи.

Приведем алгоритм и программу обработки данных, составлен­ные в точном соответствии с выбранным сценарием и методом решения:

АлгоритмПрограмма

алг «среднее арифметическое» ' среднее арифметическое

нач cls

вывод («среднее N чисел»)? «среднее N чисел»

запрос («чисел=», N) input «чисел=», N

S:= 0 S = 0

если N <= 0 то if N <= 0 then

вывод («недопустимо N»)? «недопустимо N»

инеc N > 0 то elseif N > 0 then

от k = 1 до N цикл for k = 1 to N

вывод (k, «:»)? k, «:»

запрос (x) input x

S:= S + x S = S + x

кцикл next k

s:= S/N s = S/N

вывод («среднее =», s)? «среднее=», s

все end if

кон end

При решении сложных задач для проверки правильности состав­ляемых алгоритмов и программ обязательны не только математичес­кое описание постановки задач, но и описание выбранных методов решения.

Приведем пример разработки программы обработки данных с математической постановкой задачи и полным описанием метода решения.

Третья задача: определение самого легкого из учеников по данным из таблицы, содержащей N строк:

Дата добавления: 2014-11-25