Постановка методы

Кон

Нач

Кон

Все

Все

Нач

если а ¹ О то при а ¹ 0

D: = b*b - 4*а*с D = b² - 4×а×с

если D > = 0 то при D >= 0

х1: = (-b + 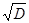)/(2*a) х₁ = (-b + 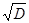)/(2×a)

х2: = (-b - 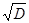)/(2*a) х₂ = (-b - 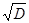)/(2×a)

инеc а = 0 то при а = 0

если b ¹ 0 при b ¹ 0

х 1: = -c/b x_l = -c/b

Результаты выполнения алгоритма приведены справа. Можно заметить, что результаты выполнения совпадают с описанием вы­бранного метода решения с помощью дискриминанта. Это позволяет утверждать, что алгоритм - правильный.

Алгоритм содержит ошибки, если можно указать допустимые ис­ходные данные, при которых либо будут получены неправильные результаты, либо результаты не будут получены вовсе. Использование алгоритмов, содержащих ошибки, приводит к созданию программ, также содержащих ошибки.

Алгоритм считается правильным, если он дает правильные резуль­таты для любых допустимых исходных данных. Правильность алго­ритмов решения прикладных задач и наличие в них ошибок можно проверять двумя основными способами.

Первый способ - проверка основных этапов построения алго­ритма:

задача ® постановка ® метод ® алгоритм

Второй способ - анализ результатов выполнения алгоритмов и их сравнение с выбранными методами решения и постановкой задачи:

задача постановка метод алгоритм

Приведем пример построения алгоритма с одновременным ана­лизом его правильности.

Задача: Определить периметр треугольника, заданного на плос­кости координатами вершин.

X_С,У_С

X_А,У_А Xв,Ув

Постановка задачи

Определение периметра треугольника, заданного на плоскости.

Дано: А = (x_А, y_А)

В = (x_В, y_В) - координаты вершин треугольника

С = (x_С,y_С)

Треб.: Р - периметр

Метод решения

Р = L_АВ +L_ВС+L_СА

L_АВ = ,

L_ВС =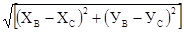

L_СА =

где: Р = L(A,B) + L(B,C) + L(C,A);

здесь L[(x,y),(u,v)] = .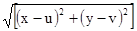

Приведем алгоритм, полученный из описания метода упорядоче­нием операций вычисления длин сторон треугольника с заверша­ющим вычислением периметра. Результаты выполнения алгоритма приведены справа.

алг «периметр треугольника»

LAB: =

LBC: =

LCA: =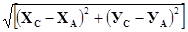

Р:= LAB + LBC + LCA

Результаты

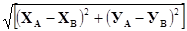
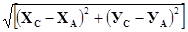
Р = LAB + LBC + LCA

Сравнение результатов выполнения алгоритма с описанием метода решения показывает, что это одна и та же система формул, что подтверждает правильность алгоритма.

Систематические методы анализа правильности алгоритмов и программ опираются на сопоставление тех же самых описаний, которые используются при их систематическом составлении.

Анализ правильности:

задача способ

¯ ¯

¯ ¯

Дата добавления: 2014-11-25