Программа. Анализ правильности алгоритмов

Анализ правильности алгоритмов

Задачи

Вопросы

1. Что такое постановка задачи?

2. Что включается в постановку задач?

3. Что такое способ решения?

4. Что такое метод решения?

5. Каков порядок решения новых задач?

6. Что такое систематическая разработка алгоритмов и программ?

1. Приведите постановку задачи, сценарий, алгоритм и программу подсчета сумм:

а) нечетных чисел;

б) квадратов целых чисел;

в) кубов целых чисел.

2. Приведите постановку задачи, сценарий, алгоритм и программу подсчета сумм:

а) членов арифметической прогрессии;

б) членов геометрической прогрессии.

3. Для последовательности чисел х₁, х₂..., х_N приведите постановку задачи, составьте сценарий, алгоритм решения и программу:

а) подсчета суммы всех чисел;

б) вычисления среднего арифметического чисел;

в) определения наибольшего из чисел;

г) определения наименьшего из чисел.

4. Для данных об учениках, содержащих сведения об их росте и весе, приведите постановку задачи, составьте сценарий, алгоритм и програм­му определения:

а) самого высокого ученика; г) самого легкого ученика;

б) самого низкого ученика; д) средний рост учеников;

в) самого тяжелого ученика; е) средний вес учеников.

5. Для данных о днях рождения своих друзей и родных приведите постановку задачи, составьте сценарий, алгоритм решения и программу:

а) определения ровесников;

б) определения людей, родившихся в один день;

в) самого молодого из своих друзей и родных;

г) самого старшего из своих родных и друзей.

На практике часто приходится встречаться с программами, со­держащими ошибки. Например, в сети Интернет можно указать много зарубежных и отечественных сайтов, которые время от времени дают сбои.

Программа содержит ошибки, если ее выполнение на ЭВМ при­водит к получению сбоев, отказов или неправильных результатов. Программу в таком состоянии нельзя использовать для решения практических задач.

Проявления ошибок:

¯

данные ® ЭВМ ® { отказ | сбой | ошибка }

Отказ - это ситуация, когда выполнение программы прекраща­ется вообще. Программы, содержащие такого рода ошибки считаются неработоспособными, и от их использования следует отказываться.

Сбой - это потеря части данных либо получение непредусмот­ренных данных. Такого рода ошибки говорят о их частичной нера­ботоспособности программ либо об их недостаточной надежности.

Результат неправильный, если он не соответствует требованиям, предъявляемым к работе программ. Программы, содержащие такие ошибки, считаются работоспособными, но их применение может приводить к получению ошибочных результатов, сбоев или отказов.

Оценка программ:

Задача

исходное требуемое

данные ® программа ® результаты

О правильности программ нельзя утверждать ничего если неиз­вестны предъявляемые к ним требования. Только при наличии стро­гих, четких спецификаций можно судить о правильности работы программ.

В качестве примера рассмотрим решение квадратного уравнения:

х² + 3×х + 2 = 0.

Исходные данные - коэффициенты а = 1, b = 3, с = 2. Требу­емые результаты - пара чисел х₁ и x₂, являющихся корнями уравне­ния. Посмотрим, будут ли корнями уравнения пары чисел:

а) х₁ = 2, x₂ = 3;б) x₁ = -2, x₂ = -3.

Решением уравнений являются числа, подстановка которых пре­вращает уравнение в тождество. В первом случае подстановка чисел х₁ = 2, х₂ = 3 в уравнение дает:

2² + 3×2 + 2 = 12 ¹ 0 - неправильно,

3² +3×3+2 = 20 ¹ 0 - неправильно.

Следовательно, числа х₁ = 2, х₂ = 3 не являются правильными результатами.

Подстановка в уравнение чисел х₁ = -2, х₂ = -3:

(-2)² + 3×(-2) +2 = 0- правильно;

(-3)² + 3×(-3) +2 = 0- правильно.

Следовательно, числа х₁ = -2, х₂ = -3 являются правильными результатами.

Приведем формальную постановку задачи решения квадратных уравнений.

Постановка задачи

Решение квадратного уравнения

а×х² + b×x + с = 0.

Дано: a, b, с - коэффициенты.

Треб.: х₁, х₂ - корни.

Где: а×х₁² + b×х₁ + с = 0.

а×х₂² + b×х₂ + с = 0.

При: а ¹ 0.

Наличие точной постановки задач позволяет говорить о правиль­ности не только конечных результатов, но и различных способов и методов их решения.

Способ правильный, если он дает правильные результаты. Способ неправильный, если он дает неправильные результаты или не дает результатов вообще.

Метод неправильный, если существуют допустимые данные, для которых он дает неправильные результаты либо не дает результатов вообще.

Метод правильный, если он дает правильные результаты для любой задачи данного класса. Использование правильных методов служит основой для составления алгоритмов и программ, не содер­жащих ошибок.

В рассматриваемом примере решения квадратных уравнений об­щим методом является вычисление корней с помощью дискрими­нанта.

Метод решения

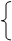x₁ = (-b + 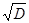)/(2×а)

x₂ = (-b - 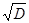)/(2×a)

где

{ D = b² - 4×а×с.

Правильность общих методов проверяется подстановкой расчет­ных формул в исходное уравнение. Получение тождеств в результате подстановок говорит о правильности выбранных расчетных формул.

Для первого корня х₁ = (-b + 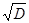)/(2×a) подстановка и тождест­венные преобразования формул дадут:

а×х₁² + b×х₁ + с =

= а×[(-b + 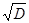)/(2×а)]² + b× (-b + 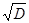)/(2×a) + с =

= (-b + 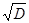)²/(4×а) + b× (-b + 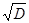)/(2×a) + с = (b + 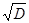) × (-b + 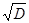)/(4×а) + с =

= (-b² + D)/(4×a) + с = (-b² + b² - 4×а×с)/(4×а) + с = -4×а×с/(4×а) + с = 0.

Аналогичные результаты получаются и при подстановке формулы второго корня х₂ = (-b - 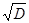)/(2×a). После выполнения анало­гичных преобразований будет получено такое же тождество. И на основании этих проверок можно сделать заключение, что рассмот­ренный метод дает правильные результаты для любык допустимых данных.

Однако саму постановку задачи необходимо дополнить условием: b² - 4×а×с ³ 0. При нарушении этого условия не только уравнение не имеет решений, но и метод решения также не дает результатов из-за необходимости вычисления корней от отрицательного дискриминан­та: D < 0.

В силу выбранного метода решения и принятой постановки алго­ритм решения квадратных уравнений приобретает следующий вид:

алг «квадратное уравнение» Результаты вычислений

Дата добавления: 2014-11-25