КУРС ФИЗИКИ 8 страница

Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одно­атомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку D S (рис. 64) и вычислим давление, оказываемое на эту площадку. При каждом соударении молеку­ла, движущаяся перпендикулярно площадке, передает ей импульс m ₀ v – (– m ₀ v) = 2 m ₀ v, где m ₀ — масса молекулы, v — ее скорость. За время D t площадки D S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием D S и высотой v D t (рис. 64). Число этих молекул равно n D Sv D t (n — концентрация молекул).

Необходимо, однако, учитывать, что реально молекулы движутся к площадке D S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется ¹/₃ молекул, причем половина молекул ¹/₆ движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку D S будет ¹/₆ n D Sv D t. При столкновении с площадкой эти молекулы передадут ей импульс

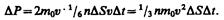
Тогда давление газа, оказываемое им на стенку сосуда,

(43.1)

Если газ в объеме V содержит N молекул, движущихся со скоростями v ₁, v ₂ ,..., v_N, то целесообразно рассматривать среднюю квадратную скорость

(43.2)

характеризующую всю совокупность молекул газа.

Уравнение (43.1) с учетом (43.2) примет вид

(43.3)

Выражение (43.3) называется основным уравнением молекулярно-кинетической те­ории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.

Учитывая, что n =N / V, получим

(43.4)

или

(43.5)

где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.

Так как масса газа m=Nm ₀, то уравнение (43.4) можно переписать в виде

Для одного моля газа т=М (М — молярная масса), поэтому

где V _m — молярный объем. С другой стороны, по уравнению Клапейрона — Менделе­ева, pV _m =RT. Таким образом,

откуда

(43.6)

Так как M=m ₀ N _А, где т ₀ — масса одной молекулы, a N _А — постоянная Авогадро, то из уравнения (43.6) следует, что

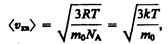(43.7)

где k=R/N _А — постоянная Больцмана. Отсюда найдем, что при комнатной температу­ре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водоро­да — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.

Средняя кинетическая энергия поступательного движения одной молекулы идеаль­ного газа

(43.8)

(использовали формулы (43.5) и (43.7)) пропорциональна термодинамической тем­пературе и зависит только от нее. Из этого уравнения следует, что при Т =0 <e₀>=0, т. е. при 0К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (43.8) раскрывает молекулярно-кинетическое толкование температуры.

§ 44. Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения

При выводе основного уравнения молекулярно-кинетической теории молекулам зада­вали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направ­лении в среднем движется одинаковое число молекул.

По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой т ₀ в газе, находящемся в состоянии равновесия при Т = const. остается постоянной и равной

Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоро­стям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Пред­полагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f (v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные d v, то на каждый интервал скорости будет приходиться некоторое число молекул d N(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул d N(v)/N, скорости которых лежат в интервале от v до v+ d v, т. е.

откуда

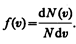
Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям:

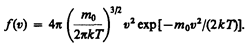(44.1)

Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).

График функции (44.1) приведен на рис. 65. Так как при возрастании v множитель exp[ –m ₀ v²/(2kT) ] уменьшается быстрее, чем растет множитель v ², то функция f(v), начинаясь от нуля, достигает максимума при v _B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно v _B.

Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+ d v, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки

Скорость, при которой функция распределения молекул идеального газа по скоро­стям максимальна, называется наиболее вероятной скоростью. Значение наиболее веро­ятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v):

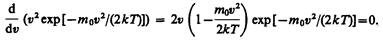
Значения v= 0 и v =¥ соответствуют минимумам выражения (44.1), а значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v _B:

(44.2)

Из формулы (44.2) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, оста­ется неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Средняя скорость молекулы < v > (средняя арифметическая скорость) определяется по формуле

Подставляя сюда f(v) и интегрируя, получаем

(44.3)

Скорости, характеризующие состояние газа: 1) наиболее вероятная 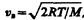2) средняя 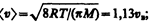3) средняя квадратичная (рис. 65). Исходя из распределения молекул по скоростям

(44.4)

можно найти распределение молекул газа по значениям кинетической энергии e. Для этого перейдем от переменной v к переменной e =m ₀ v ² / 2. Подставив в (44.4) v= и d v= 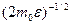d e, получим

где d N (e) — число молекул, имеющих кинетическую энергию поступательного движе­ния, заключенную в интервале от e до e + d e.

Таким образом, функция распределения молекул по энергиям теплового движения

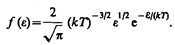
Средняя кинетическая энергия < e > молекулы идеального газа

т. е. получили результат, совпадающий с формулой (43.8).

§ 45. Барометрическая формула. Распределение Больцмана

При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р (рис. 67), то на высоте h+ d h оно равно p+ d p (при d h >0 d p <0, так как давление с высотой убывает). Разность давлений р и p+ d p равна весу газа, заключенного в объеме цилиндра высотой d h с основанием площадью 1 м²:

где r — плотность газа на высоте h (d h настолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно,

(45.1)

Воспользовавшись уравнением состояния идеального газа pV=(m/M) RT (т — масса газа, М — молярная масса газа), находим, что

Подставив это выражение в (45.1), получим

С изменением высоты от h ₁ до h ₂ давление изменяется от р ₁ до р ₂ (рис. 67), т. е.

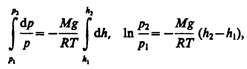
или

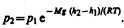(45.2)

Выражение (45.2) называется барометрической формулой. Она позволяет найти атмос­ферное давление в зависимости от высоты или, измерив давление, найти высоту: Так как высоты обозначаются относительно уровня моря, где давление считается нормаль­ным, то выражение (45.2) может быть записано в виде

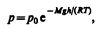(45.3)

где р — давление на высоте h.

Прибор для определения высоты над земной поверхностью называется высотоме­ром (или альтиметром). Его работа основана на использовании формулы (45.3). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.

Барометрическую формулу (45.3) можно преобразовать, если воспользоваться вы­ражением (42.6) p=nkT:

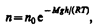
где n – концентрация молекул на высоте h, n ₀ – то же, на высоте h= 0. Так как M =m ₀ N _A (N _A – постоянная Авогадро, т ₀ – масса одной молекулы), a R=kN _A, то

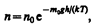(45.4)

где m ₀ gh =П — потенциальная энергия молекулы в поле тяготения, т. е.

(45.5)

Выражение (45.5) называется распределением Больцмана для внешнего потенциаль­ного поля. Из вето следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана (45.5) справедливо в любом вне­шнем потенциальном поле, а не только в поле сил тяжести.

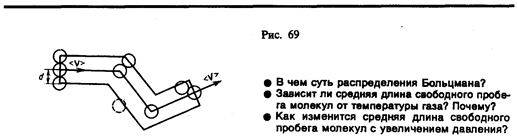
§ 46. Среднее число столкновений и средняя длина свободного пробега молекул

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкивают­ся друг с другом. Между двумя последовательными столкновениями молекулы прохо­дят некоторый путь l, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул < l >.

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 68). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).

Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости < v >, и если < z > — среднее число столкновений, испытываемых одной молеку­лой газа за 1 с, то средняя длина свободного пробега

Для определения <z> представим себе молекулу в виде шарика диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. 69).

Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра:

где п — концентрация молекул, V = pd ² < v > < v > — средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом, среднее число столкновений

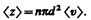
Расчеты показывают, что при учете движения других молекул

Тогда средняя длина свободного пробега

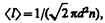
т. е. < l > обратно пропорциональна концентрации n молекул. С другой стороны, из (42.6) следует, что при постоянной температуре n пропорциональна давлению р. Следовательно,

§ 47. Опытное обоснование молекулярно-кинетической теории

Рассмотрим некоторые явления, экспериментально подтверждающие основные поло­жения и выводы молекулярно-кинетической теории.

1. Броуновское движение. Шотландский ботаник Р. Броун (1773—1858), наблюдая под микроскопом взвесь цветочной пыльцы в воде, обнаружил, что частицы пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места на место, подобно пылинкам в солнечном луче. Впоследствии оказалось, что подобное сложное зигзагообразное движение характерно для любых частиц малых размеров (»1 мкм), взвешенных в газе или жидкости. Интенсивность этого движения, называемого броуновским, повышается с ростом температуры среды, с уменьшением вязкости и раз­меров частиц (независимо от их химической природы). Причина броуновского движе­ния долго оставалась неясной. Лишь через 80 лет после обнаружения этого эффекта ему было дано объяснение: броуновское движение взвешенных частиц вызывается ударами молекул среды, в которой частицы взвешены. Так как молекулы движутся хаотически, то броуновские частицы получают толчки с разных сторон, поэтому и совершают движение столь причудливой формы. Таким образом, броуновское движение является подтверждением выводов молекулярно-кинетической теории о хаотическом (тепловом) движении атомов и молекул.

2. Опыт Штерна. Первое экспериментальное определение скоростей молекул выпо­лнено немецким физиком О. Штерном (1888—1970). Его опыты позволили также оценить распределение молекул по скоростям. Схема установки Штерна представлена на рис. 70. Вдоль оси внутреннего цилиндра с щелью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе. При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра, давая изображение щели О. Если прибор привести во вращение вокруг общей оси цилиндров, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние s. Изображение щели получается размытым. Исследуя толщину осажденного слоя, можно оценить распределение моле­кул по скоростям, которое соответствует максвелловскому распределению.

Зная радиусы цилиндров, их угловую скорость вращения, а также измеряя s, можно вычислить скорость движения атомов серебра при данной температуре проволоки. Результаты опыта показали, что средняя скорость атомов серебра близка к той, которая следует из максвелловского распределения молекул по скоростям.

3. Опыт Ламмерт. Этот опыт позволяет более точно определить закон распределе­ния молекул по скоростям. Схема вакуумной установки приведена на рис. 71. Молеку­лярный пучок, сформированный источником, проходя через щель, попадает в прием­ник. Между источником и приемником помещают два диска с прорезями, закреплен­ных на общей оси. При неподвижных дисках молекулы достигают приемника, проходя через прорези в обоих дисках. Если ось привести во вращение, то приемника достигнут только те прошедшие прорезь в первом диске молекулы, которые затрачивают для пробега между дисками время, равное или кратное времени оборота диска. Другие же молекулы задерживаются вторым диском. Меняя угловую скорость вращения дисков и измеряя число молекул, попадающих в приемник, можно выявить закон распределе­ния молекул по скоростям. Этот опыт также подтвердил справедливость максвелловс­кого распределения молекул по скоростям.

4. Опытное определение постоянной Авогадро. Воспользовавшись идеей распределе­ния молекул по высоте (см. формулу (45.4)), французский ученый Ж. Перрен (1870—1942) экспериментально определил значение постоянной Авогадро. Исследуя под микроскопом броуновское движение, он убедился, что броуновские частицы рас­пределяются по высоте подобно молекулам газа в поле тяготения. Применив к ним больцмановское распределение, можно записать

где т— масса частицы, т ₁ — масса вытесненной ею жидкости; m= ⁴/₃ pr ³ r, m ₁ = ⁴/₃ pr ³ r ₁ (r — радиус частицы, r — плотность частицы, r ₁ — плотность жидкости).

Если n ₁ и n ₂ — концентрации частиц на уровнях h ₁ и n ₂, a k=R/N _A, то

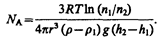
Значение N _A, получаемое из работ Ж. Перрена, соответствовало значениям, полу­ченным в других опытах, что подтверждает применимость к броуновским частицам распределения (45.4).

§ 48. Явления переноса в термодинамически неравновесных системах

В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространствен­ный перенос энергии, массы, импульса. К явлениям переноса относятся теплопровод­ность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномер­ными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориен­тирована в направлении переноса.

1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше,чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.

Перенос энергии в форме теплоты подчиняется закону Фурье:

(48.1)

где j_E — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, l — теплопроводность, 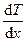— градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки j_E и 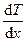– противоположны). Теплопроводность l численно равна плотности теплового потока при градиенте температуры, равном единице.

Можно показать, что

(48.2)

где с_V — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), r — плотность газа, < v > — средняя скорость теплового движения молекул, < l > — средняя длина сво­бодного пробега.

2. Диффузия. Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жид­костей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

Явление диффузии для химически однородного газа подчиняется закону Фука:

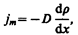(48.3)

где j_m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), d r/ d x — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки j_m и d r/ d x противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинети­ческой теории газов,

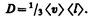(48.4)

3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

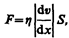(48.5)

где h — динамическая вязкость (вязкость), d v/ d x — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматри­вать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно пред­ставить в виде

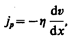(48.6)

где j_p — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки j_р и противоположны).

Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле

Дата добавления: 2014-11-25