КУРС ФИЗИКИ 18 страница

12.3. По медному проводу сечением 0,3 мм² течет ток 0,3 А. Определить силу, действую­щую на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление меди 17 нОм×м. [2,72×10^–21 Н]

12.4. Сила тока в проводнике сопротивлением 10 Ом равномерно убывает от I ₀=3 А до I =0 за 30 с. Определить выделившееся за это время в проводнике количество теплоты. [900 Дж].

12.5. Плотность электрического тока в алюминиевом проводе равна 5 А/см². Определить удель­ную тепловую мощность тока, если удельное сопротивление алюминия 26 нОм×м. [66 Дж/(м³×с)]

12.6. Определить внутреннее сопротивление r источника тока, если во внешней цепи при силе тока I ₁=5 А выделяется мощность P ₁=10 Вт, а при силе тока I ₂=8 А — мощность P ₂=12 Вт. [0,17 Ом]

12.7. Три источника тока с э.д.с. E ₁=1,8 В, E ₂=1,4 В и E ₃=1,1 В соединены накоротко одно­именными полюсами. Внутреннее сопротивление первого источника r ₁=0,4 Ом, второ­го — r ₂=0,6 Ом. Определить внутреннее сопротивление третьего источника, если через первый источник идет ток I ₁=1,13 A. [0,2 Ом]

Глава 13 Электрические токи в металлах, вакууме и газах

§ 102. Элементарная классическая теория электропроводности металлов

Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости метал­лов, созданной немецким физиком П. Друде (1863—1906) и разработанной впоследст­вии нидерландским физиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории.

Первый из таких опытов — опыт Рикке * (1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, Аl, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (»3,5×10⁶ Кл), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856—1940) электроны.

*К. Рикке (1845—1915) — немецкий физик.

Для доказательства этого предположения необходимо было определить знак и ве­личину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед,как смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат российским физикам С. Л. Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947). Эти опы­ты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881—1948) и ранее шотландским физиком Б. Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах имеют отрицательный заряд, а их удельный заряд приблизительно одинаков для всех исследованных метал­лов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали. Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны.

Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атом­ными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электро­ны, образуя своеобразный электронный газ, обладающий, согласно электронной те­ории металлов, свойствами идеального газа.

Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По теории Друде—Лоренца, электроны обладают такой же энергией теплового движения,как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории (см. (44.3)), можно найти среднюю скорость теплового движения электронов

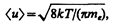
которая для T =300 К равна 1,1×10⁵ м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.

При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость á v ñ упорядоченного движения электронов мож­но оценить согласно формуле (96.1) для плотности тока: j = пe á v ñ. Выбрав допустимую плотность тока, например для медных проводов 10⁷ А/м², получим, что при концент­рации носителей тока n = 8×10²⁸м^–3 средняя скорость á v ñ упорядоченного движения электронов равна 7,8×10^–4 м/с. Следовательно, á v ñ<<á u ñ, т. е. даже при очень боль­ших плотностях тока средняя скорость упорядоченного движения электронов, обуслов­ливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость á v ñ + á u ñ можно заменять скоростью теплового движения á u ñ.

Казалось бы, полученный результат противоречит факту практически мгновенной передачи электрических сигналов на большие расстояния. Дело в том, что замыкание электрической цепи влечет за собой распространение электрического поля со скоро­стью с (c =3×10⁸м/с). Через время t = l / c (l — длина цепи) вдоль цепи установится стационарное электрическое поле и в ней начнется упорядоченное движение электро­нов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.

§ 103. Вывод основных законов электрического тока в классической теории электропроводности металлов

1. Закон Ома. Пусть в металлическом проводнике существует электрическое поле напряженностью E =const. Co стороны поля заряд е испытывает действие силы F = eE и приобретает ускорение a=F/m=eE/m. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость

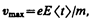
где á t ñ — среднее время между двумя последовательными соударениями электрона с ионами решетки.

Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с иона­ми решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядочен­ного движения становится равной нулю. Следовательно, средняя скорость направлен­ного движения электрона

(103.1)

Классическая теория металлов не учитывает распределения электронов по скоро­стям, поэтому среднее время á t ñ свободного пробега определяется средней длиной свободного пробега á l ñ и средней скоростью движения электронов относительно кристаллической решетки проводника, равной á u ñ + á v ñ (á u ñ — средняя скорость теп­лового движения электронов). В § 102 было показано, что á v ñ<<á u ñ, поэтому

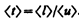
Подставив значение á t ñ в формулу (103.1), получим

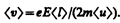
Плотность тока в металлическом проводнике, по (96.1),

откуда видно, что плотность тока пропорциональна напряженности поля, т. е. получи­ли закон Ома в дифференциальной форме (ср. с (98.4)). Коэффициент пропорциональ­ности между j и E есть не что иное, как удельная проводимость материала

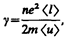(103.2)

которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.

2. Закон Джоуля — Ленца. К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию

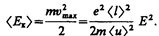(103.3)

При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.

За единицу времени электрон испытывает с узлами решетки в среднем á z ñ сто­лкновений:

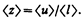(103.4)

Если n — концентрация электронов, то в единицу времени происходит п á z ñ столкнове­ний и решетке передается энергия

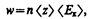(103.5)

которая идет на нагревание проводника. Подставив (103.3) и (103.4) в (103.5), получим таким образом энергию, передаваемую решетке в единице объема проводника за единицу времени,

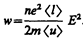(103.6)

Величина w является удельной тепловой мощностью тока (см. § 99). Коэффициент пропорциональности между w и E ² по (103.2) есть удельная проводимость g; следовате­льно, выражение (103.6)—закон Джоуля—Ленца в дифференциальной форме (ср. с (99.7)).

3. Закон Видемана — Франца. Металлы обладаюткак большой электропровод­ностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы—свободные электроны, которые, перемещаясь в металле, переносят не только электрический заряд, но и присущую им энергию хаотического (теплового) движения, т. е. осуществляют перенос теплоты.

Видеманом и Францем в 1853 г. экспериментально установлен закон, согласно которому отношение теплопроводности (l) к удельной проводимости (g) для всех металлов при одной и той же температуре одинаково и увеличивается пропорциональ­но термодинамической температуре:

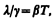
где b — постоянная, не зависящая от рода металла.

Элементарная классическая теория электропроводности металлов позволила найти значение b: b =3 (k/e) ², где k— постоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным случайно. Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов по скоростям, получил b =2 (k/e) ², что привело к резкому расхождению теории с опытом.

Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Видемана — Франца. Однако она помимо рассмотренных противоречий в законе Видемана — Франца столкнулась еще с рядом трудностей при объяснении различных опыт­ных данных. Рассмотрим некоторые из них.

Температурная зависимость сопротивления. Из формулы удельной проводимости (103.2) следует, что сопротивление металлов, т. е. величина, обратно пропорциональ­ная g, должна возрастать пропорционально 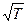(в (103.2) п и á l ñ от температуры не зависят, а á u ñ~ 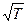). Этот вывод электронной теории противоречит опытным данным, согласно которым R ~ T (см. § 98).

Оценка средней длины свободного пробега электронов в металлах. Чтобы по фор­муле (103.2) получить g, совпадающие с опытными значениями, надо принимать á l ñ значительно больше истинных, иными словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Со­гласно закону Дюлонга и Пти (см. § 73), теплоемкость одноатомного кристалла равна 3 R. Учтем, что теплоемкость одноатомного электронного газа равна ³ / ₂ R. Тогда атомная теплоемкость металлов должна быть близка к 4,5 R. Однако опыт доказывает, что она равна 3 R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классичес­кой электронной теорией.

Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности метал­лов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, таккак во многих случаях (например, при малой концент­рации электронов проводимости и высокой температуре) она дает правильные качест­венные результаты и является по сравнению с квантовой теорией простой и нагляд­ной.

§ 104. Работа выхода электронов из металла

Как показывает опыт, свободные электроны при обычных температурах практически не покидают металл. Следовательно, в поверхностном слое металла должно быть задерживающее электрическое поле, препятствующее выходу электронов из металла в окружающий вакуум. Работа, которую нужно затратить для удаления электрона из металла в вакуум, называется работой выхода. Укажем две вероятные причины появле­ния работы выхода:

1. Если электрон по какой-то причине удаляется из металла, то в том месте, которое электрон покинул, возникает избыточный положительный заряд и электрон притягивается к индуцированному им самим положительному заряду.

2. Отдельные электроны, покидая металл, удаляются от него на расстояния порядка атомных и создают тем самым над поверхностью металла «электронное облако», плотность которого быстро убывает с расстоянием. Это облако вместе с наружным слоем положительных ионов решетки образует двойной электрический слой, поле которого подобно полю плоского конденсатора. Толщина этого слоя равна нескольким межатомным расстояниям (10^–10—10^–9 м). Он не создает электрического поля во внешнем пространстве, но препятствует выходу свободных электронов из металла.

Таким образом, электрон при вылете из металла должен преодолеть задержива­ющее его электрическое поле двойного слоя. Разность потенциалов D j в этом слое, называемая поверхностным скачком потенциала, определяется работой выхода (А)электрона из металла:

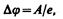
где е — заряд электрона. Так как вне двойного слоя электрическое поле отсутствует, то потенциал среды равен нулю, а внутри металла потенциал положителен и равен D j. Потенциальная энергия свободного электрона внутри металла равна — е D j и является относительно вакуума отрицательной. Исходя из этого можно считать, что весь объем металла для электронов проводимости представляет потенциальную яму с плоским дном, глубина которой равна работе выхода А.

Работа выхода выражается в электрон-вольтах (эВ): 1 эВ равен работе, соверша­емой силами поля при перемещении элементарного электрического заряда (заряда, равного заряду электрона) при прохождении им разности потенциалов в 1 В. Так как заряд электрона равен 1,6×10^–19 Кл, то 1 эВ= 1,6×10^–19 Дж.

Работа выхода зависит от химической природы металлов и от чистоты их поверх­ности и колеблется в пределах нескольких электрон-вольт (например, у калия A = 2,2 эВ, у платины A =6,3 эВ). Подобрав определенным образом покрытие поверх­ности, можно значительно уменьшить работу выхода. Например, если нанести на поверхность вольфрама (А = 4,5 эВ) слой оксида щелочно-земельного металла (Са, Sr, Ва), то работа выхода снижается до 2 эВ.

§ 105. Эмиссионные явления и их применение

Если сообщить электронам в металлах энергию, необходимую для преодоления рабо­ты выхода, то часть электронов может покинуть металл, в результате чего наблюдает­ся явление испускания электронов, или электронной эмиссии. В зависимости от способа сообщения электронам энергии различают термоэлектронную, фотоэлектронную, вто­ричную электронную и автоэлектронную эмиссии.

1. Термоэлектронная эмиссия — это испускание электронов нагретыми металлами. Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энерги­ям) некоторые электроны обладают энергией, достаточной для преодоления потенци­ального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет и явление термоэлектронной эмиссии становится заметным.

Исследование закономерностей термоэлектронной эмиссии можно провести с по­мощью простейшей двухэлектродной лампы — вакуумного диода, представляющего собой откачанный баллон, содержащий два электрода: катод K и анод А. В простейшем случае катодом служит нить из тугоплавкого металла (например, вольфрама), накали­ваемая электрическим током. Анод чаще всего имеет форму металлического цилиндра, окружающего катод. Если диод включить в цепь, как это показано на рис. 152, то при накаливании катода и подаче на анод положительного напряжения (относительно катода) в анодной цепи диода возникает ток. Если поменять полярность батареи Б _а, то ток прекращается, как бы сильно катод ни накаливали. Следовательно, катод испускает отрицательные частицы — электроны.

Если поддерживать температуру накаленного катода постоянной и снять зависи­мость анодного тока I _а от анодного напряжения U _а, — вольт-амперную характеристику (рис. 153), то оказывается, что она не является линейной, т. е. для вакуумного диода закон Ома не выполняется. Зависимость термоэлектронного тока I от анодного напряжения в области малых положительных значений U описывается законом трех вторых (установлен русским физиком С. А. Богуславским (1883—1923) и американским физиком И. Ленгмюром (1881—1957)):

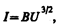
где В— коэффициент, зависящий от формы и размеров электродов, а также их взаимного расположения.

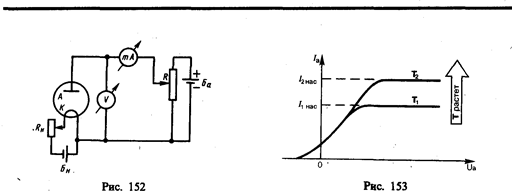
При увеличении анодного напряжения ток возрастает до некоторого максималь­ного значения I _нас, называемого током насыщения. Это означает, что почти все электро­ны, покидающие катод, достигают анода, поэтому дальнейшее увеличение напряжен­ности поля не может привести к увеличению термоэлектронного тока. Следовательно, плотность тока насыщения характеризует эмиссионную способность материала катода.

Плотность тока насыщения определяется формулой Ричардсона — Дешмана, выве­денной теоретически на основе квантовой статистики:

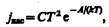
где А — работа выхода электронов из катода, T — термодинамическая температура, С — постоянная, теоретически одинаковая доя всех металлов (это не подтверждается экспериментом, что, по-видимому, объясняется поверхностными эффектами). Умень­шение работы выхода приводит к резкому увеличению плотности тока насыщения. Поэтому применяются оксидные катоды (например, никель, покрытый оксидом щелочно-земельного металла), работа выхода которых равна 1—1,5 эВ.

На рис. 153 представлены вольт-амперные характеристики для двух температур катода: Т ₁ и T ₂, причем Т ₂ >Т ₁. С повышением температуры катода испускание электронов с катода интенсивнее, при этом увеличивается и ток насыщения. При U _а=0 наблюдается анодный ток, т. е. некоторые электроны, эмиттируемые катодом, облада­ют энергией, достаточной для преодоления работы выхода и достижения анода без приложения электрического поля.

Явление термоэлектронной эмиссии используется в приборах, в которых необ­ходимо получить поток электронов в вакууме, например в электронных лампах, рентгеновских трубках, электронных микроскопах и т. д. Электронные лампы широко применяются в электро- и радиотехнике, автоматике и телемеханике для выпрямления переменных токов, усиления электрических сигналов и переменных токов, генерирова­ния электромагнитных колебаний в т. д. В зависимости от назначения в лампах используются дополнительные управляющие электроды.

2. Фотоэлектронная эмиссия — это эмиссия электронов из металла под действием света, а также коротковолнового электромагнитного излучения (например, рентгеновс­кого). Основные закономерности этого явления будут разобраны при рассмотрении фотоэлектрического эффекта.

3. Вторичная электронная эмиссия — это испускание электронов поверхностью ме­таллов, полупроводников или диэлектриков при бомбардировке их пучком электронов. Вторичный электронный поток состоит из электронов, отраженных поверхностью (упруго и неупруго отраженные электроны), и «истинно» вторичных электронов — эле­ктронов, выбитых из металла, полупроводника или диэлектрика первичными электро­нами.

Отношение числа вторичных электронов n ₂ к числу первичных n ₁, вызвавших эмиссию, называется коэффициентом вторичной электронной эмиссии:

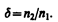
Коэффициент d зависит от природы материала поверхности, энергии бомбардирующих частиц и их угла падения на поверхность. У полупроводников и диэлектриков d боль­ше,чем у металлов. Это объясняется тем, что в металлах, где концентрация электронов проводимости велика, вторичные электроны, часто сталкиваясь с ними, теряют свою энергию и не могут выйти из металла. В полупроводниках и диэлектриках же из-за малой концентрации электронов проводимости столкновения вторичных электронов с ними происходят гораздо реже и вероятность выхода вторичных электронов из эмиттера возрастает в несколько раз.

Для примера на рис. 154 приведена качественная зависимость коэффициента вто­ричной электронной эмиссии d от энергии Е падающих электронов для КСl. С увеличе­нием энергии электронов d возрастает, так как первичные электроны все глубже проникают в кристаллическую решетку и, следовательно, выбивают больше вторичных электронов. Однако при некоторой энергии первичных электронов d начинает умень­шаться. Это связано с тем, что с увеличением глубины проникновения первичных электронов вторичным все труднее вырваться на поверхность. Значение d _maxдля КCl достигает»12 (для чистых металлов оно не превышает 2).

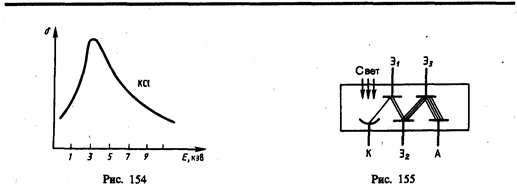
Явление вторичной электронной эмиссии используется в фотоэлектронных умножителях (ФЭУ), применимых для усиления слабых электрических токов. ФЭУ представ­ляет собой вакуумную трубку с фотокатодом К и анодом А, между которыми расположено несколько электродов — эмиттеров (рис. 155). Электроны, вырванные из фотокатода под действием света, попадают на эмиттер Э₁, пройда ускоряющую разность потенциалов между К и Э₁. Из эмиттера Э₁ выбивается d электронов. Усиленный таким образом электронный поток направляется на эмиттер Э₂, и процесс умножения повторяется на всех последующих эмиттерах. Если ФЭУ содержит n эмит­теров, то на аноде А, называемом коллектором, получается усиленный в dⁿ раз фотоэлектронный ток.

4. Автоэлектронная эмиссия — это эмиссия электронов с поверхности металлов под действием сильного внешнего электрического поля. Эти явления можно наблюдать в откачанной трубке, конфигурация электродов которой (катод — острие, анод — вну­тренняя поверхность трубки) позволяет при напряжениях примерно 10³ В получать электрические поля напряженностью примерно 10⁷ В/м. При постепенном повышении напряжения уже при напряженности поля у поверхности катода примерно 10⁵ —10⁶ В/м возникает слабый ток, обусловленный электронами, испускаемыми катодом. Сила этого тока увеличивается с повышением напряжения на трубке. Токи возникают при холодном катоде, поэтому описанное явление называется также холодной эмиссией. Объяснение механизма этого явления возможно лишь на основе квантовой теории.

§ 106. Ионизация газов. Несамостоятельный газовый разряд

Газы при не слишком высоких температурах и при давлениях, близких к атмосфер­ному, являются хорошими изоляторами. Если поместить в сухой атмосферный воздух заряженный электрометр с хорошей изоляцией, то его заряд долго остается неизмен­ным. Это объясняется тем, что газы при обычных условиях состоят из нейтральных атомов и молекул и не содержат свободных зарядов (электронов и ионов). Газ становится проводником электричества, когда некоторая часть его молекул ионизует­ся, т. е. произойдет расщепление нейтральных атомов и молекул на ионы и свободные электроны. Для этого газ надо подвергнуть действию какого-либо ионизатора (напри­мер, поднеся к заряженному электрометру пламя свечи, наблюдаем спад его заряда; здесь электропроводность газа вызвана нагреванием).

При ионизации газов, таким образом, под действием какого-либо ионизатора происходит вырывание из электронной оболочки атома или молекулы одного или нескольких электронов, что приводит к образованию свободных электронов и положи­тельных ионов. Электроны могут присоединяться к нейтральным молекулам и атомам, превращая их в отрицательные ионы. Следовательно, в ионизованном газе имеются положительные и отрицательные ионы и свободные электроны. Прохождение элект­рического тока через газы называется газовым разрядом.

Ионизация газов может происходить под действием различных ионизаторов: силь­ный нагрев (столкновения быстрых молекул становятся настолько сильными, что они разбиваются на ионы), короткое электромагнитное излучение (ультрафиолетовое, рен­тгеновское и g-излучения), корпускулярное излучение (потоки электронов, протонов, a-частиц) и т. д. Для того чтобы выбить из молекулы (атома) один электрон, необ­ходимо затратить определенную энергию, называемую энергией ионизации, значения которой для атомов различных веществ лежат в пределах 4¸25 эВ.

Одновременно с процессом ионизации газа всегда идет и обратный процесс — про­цесс рекомбинации: положительные и отрицательные ионы, положительные ионы и эле­ктроны, встречаясь, воссоединяются между собой с образованием нейтральных атомов и молекул. Чем больше ионов возникает под действием ионизатора, тем интенсивнее идет и процесс рекомбинации.

Дата добавления: 2014-11-25