КУРС ФИЗИКИ 21 страница

Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам (рис. 174). Представим себе замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касатель­ной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна

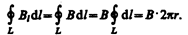
Согласно выражению (118.1), получим В× 2p r=m ₀ I (в вакууме), откуда

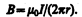
Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока, выведенное выше (см. (110.5)).

Сравнивая выражения (83.3) и (118.1) для циркуляции векторов Е и В, видим, что между ними существует принципиальное различие. Циркуляция вектора Е электростати­ческого поля всегда равна нулю, т. е. электростатическое поле является потенциаль­ным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био — Савара— Лапласа.

§ 119. Магнитные поля соленоида и тороида

Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее,тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA, как показано на рис. 175. Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно (118.1), равна

Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и B_l= 0. На участке вне соленоида B =0. На участке DA циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

(119.1)

Из (119.1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

(119.2)

Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био — Савара — Лапласа; в результате получается та же формула (119.2).

Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

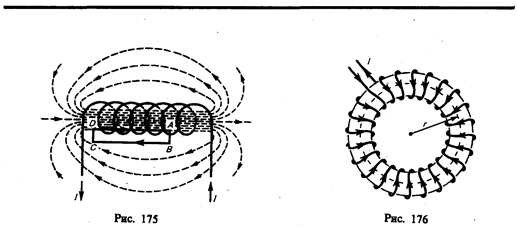
Линии магнитной индукции в данном случае, как следует из соображений симмет­рии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции (118.1), B× 2p r=m ₀ NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)

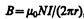
где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и B× 2p r= 0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).

§ 120. Поток вектора магнитной индукции. Теорема Гаусса для поля В

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называ­ется скалярная физическая величина, равная

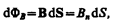(120.1)

где B_n = В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), d S =d S n — вектор, модуль которого равен d S, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos a (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено (см. § 109): оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции Ф _B через произвольную поверхность S равен

(120.2)

Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, B_n=B=const и

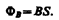
Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — маг­нитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположен­ную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл×м²).

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

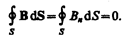(120.3)

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные выражения (см. (120.3), (81.2)).

В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницае­мостью m, согласно (119.2), равна

Магнитный поток сквозь один виток соленоида площадью S равен

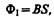
а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

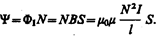(120.4)

§ 121. Работа по перемещению проводника и контура с током в магнитном поле

На проводник с током в магнитном поле действуют силы, определяемые законом Ампера (см. § 111). Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки, рис. 177), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током.

Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемещаться), помещенный в однородное внешнее магнитное поле, перпен­дикулярное плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна

Под действием этой силы проводник переместится параллельно самому себе на отрезок d x из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

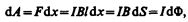
так как l d x= d S — площадь, пересекаемая проводником при его перемещении в маг­нитном поле, B d S= dФ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,

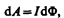(121.1)

т. е. работа по перемещению проводника с током в магнитном поле равна произведе­нию силы тока на магнитный поток, пересеченный движущимся проводником. Получен­ная формула справедлива и для произвольного направления вектора В.

Вычислим работу по перемещению замкнутого контура с постоянным то­ком I в магнитном поле. Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение М', изоб­раженное на рис. 178 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно разобьем на два соединенных своими концами проводника: AВС и CDА.

Работа d A, совершаемая силами Ампера при рассматриваемом перемещении кон­тура в магнитном поле, равна алгебраической сумме работ по перемещению провод­ников AВС (d A ₁) и CDA (d A ₂), т. е.

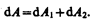(121.2)

Силы, приложенные к участку CDA контура, образуют с направлением перемеще­ния острые углы, поэтому совершаемая ими работа dA ₂ > 0.. Согласно (121.1), эта работа равна произведению силы тока I в контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ₂, пронизывающий контур в его конеч­ном положении. Следовательно,

(121.3)

Силы, действующие на участок AВС контура, образуют с направлением перемеще­ния тупые углы, поэтому совершаемая ими работа d A ₁<0. Проводник AВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ₁, пронизывающий контур в начальном положении. Следовательно,

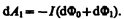(121.4)

Подставляя (121.3) и (121.4) в (121.2), получим выражение для элементарной работы:

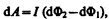
где dФ₂ — dФ₁ = dФ ' — изменение магнитного потока сквозь площадь, ограниченную контуром с током. Таким образом,

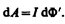(121.5)

Проинтегрировав выражение (121.5), определим работу, совершаемую силами Ампера, при конечном произвольном.перемещении контура в магнитном поле:

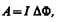(121.6)

т. е. работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Формула (121.6) остается справедливой для контура любой формы в про­извольном магнитном поле.

Задачи

14.1. Тонкое кольцо массой 15 г и радиусом 12 см несет заряд, равномерно распределенный с линейной плотностью 10 нКл/м. Кольцо равномерно вращается с частотой 8 с^–1 от­носительно оси, перпендикулярной плоскости кольца и проходящей через ее центр. Определить отношение магнитного момента кругового тока, создаваемого кольцом, к его моменту импульса. [251 нКл/кг]

14.2. По проводу, согнутому в виде квадрата со стороной, равной 60 см, течет постоянный ток 3 А. Определить индукцию магнитного поля в Центре квадрата. [5,66 мкТл]

14.3. По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми равно 25 см, текут токи 20 и 30 А в противоположных направлениях. Опреде­лить магнитную индукцию В в точке, удаленной на r ₁=30 см от первого и r ₂=40 см от второго проводника. [9,5 мкТл]

14.4. Определить магнитную индукцию на оси тонкого проволочного кольца радиусом 10 см, по которому течет ток 10 А, в точке, расположенной на расстоянии 15 см от центра кольца. [10,7 мкТл]

14.5. Два бесконечных прямолинейных параллельных проводника с одинаковыми токами, те­кущими в одном направлении, находятся друг от друга на расстоянии R. Чтобы их раздвинуть до расстояния 3 R, на каждый сантиметр длины проводника затрачивается работа A =220 нДж. Определить силу тока в проводниках. [10 А]

14.6. Определить напряженность поля, создаваемого прямолинейно равномерно движущимся со скоростью 500 км/с электроном в точке, находящейся от него на расстоянии 20 нм и лежащей на перпендикуляре к скорости, проходящем через мгновенное положение электрона. [15,9 А/м]

14.7. Протон, ускоренный разностью потенциалов 0,5 кВ, влетая в однородное магнитное поле с индукцией 0,1 Тл, движется по окружности. Определить радиус этой окружности. [3,23 см]

14.8. Определить, при какой скорости лучок заряженных частиц, проходя перпендикулярно область, в которой созданы однородные поперечные электрическое и магнитное поля с E =10 кВ/м и В= 0,2 Тл, не отклонятся. [50 км/с]

14.9. Циклотрон ускоряет протоны до энергии 10 МэВ. Определить радиус дуантов циклотрона при индукции магнитного поля 1 Тл. [>47 см]

14.10. Через сечение медной пластинки толщиной 0,1 мм пропускается ток 5 А. Пластинка помещается в однородное магнитное поле с индукцией 0,5 Тл, перпендикулярное ребру пластинки и направлению тока. Считая концентрацию электронов проводимости равной концентрации атомов, определить возникающую в пластине поперечную (холловскую) разность потенциалов. Плотность меди 8,93 г/см³. [1,85 мкВ]

14.11. По прямому бесконечно длинному проводнику течет ток 15 А. Определить, пользуясь теоремой о циркуляции вектора В, магнитную индукцию В в точке, расположенной на расстоянии 15 см от проводника. [20 мкТл]

14.12. Определить, пользуясь теоремой о циркуляции вектора В, индукцию и напряженность магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей 300 витков, протекает ток 1 А. Внешний диаметр тороида равен 60 см, внутренний — 40 см. [0,24 мТл; 191 А/м]

14.13. Поток магнитной индукции сквозь площадь поперечного сечения соленоида (без сер­дечника) Ф=5 мкВб. Длина соленоида l= 25 см. Определить магнитный момент p _m этого соленоида. [1 А×м²]

14.14. Круглая рамка с током площадью 20 см² закреплена параллельно магнитному полю (В= 0,2 Тл), и на нее действует вращающий момент 0,6 мН×м. Рамку освободили, после поворота на 90° ее угловая скорость стала 20 с^–1. Определить: 1) силу тока, текущего в рамке; 2) момент инерции рамки относительно ее диаметра. [1) 1,5 А; 2) 3×10^–6 кг×м²]

Глава 15 Электромагнитная индукция

§122. Явление электромагнитной индукции (опыты Фарадея)

В гл. 14 было показано, что электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальная задача была блестяще решена в 1831 г. английским физиком М. Фарадеем, открывшим явление электромаг­нитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Рассмотрим классические опыты Фарадея, с помощью которых было обнаружено явление электромагнитной индукции.

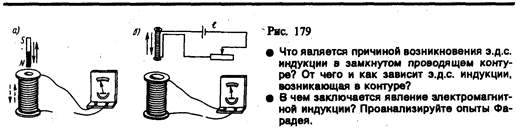
Опыт I (рис. 179, а). Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонений стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита направление отклонения стрелки изменится. Для получения индукционного тока магнит можно оставлять неподвижным, тогда нужно относительно магнита передвигать соленоид.

Опыт П. Концы одной из катушек, вставленных одна в другую, присоединяются к галь­ванометру, а через другую катушку пропускается ток. Отклонение стрелки гальванометра наблю­дается в моменты включения или выключения тока, в моменты его увеличения или уменьшения или при перемещении катушек друг относительно друга (рис. 179, б). Направления отклонений стрелки гальванометра также противоположны при включении или выключении тока, его увеличе­нии или уменьшении, сближении или удалении катушек.

Обобщая результаты своих многочисленных опытов, Фарадей пришел к выводу, что индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также возникает индукцион­ный ток. В данном случае индукция магнитного поля вблизи проводника остается постоянной, а меняется только поток магнитной индукции сквозь контур.

Опытным путем было также установлено, что значение индукционного тока совер­шенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения (в опытах Фарадея также доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше скорость движения маг­нита, или скорость изменения силы тока, или скорость движения катушек).

Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получения электрического тока с помощью магнитного поля. Этим была установлена взаимосвязь между электрическими и магнитными явлениями, что послужило в дальнейшем толчком для разработки теории электромаг­нитного поля.

§ 123. Закон Фарадея и его вывод из закона сохранения энергии

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количествен­ному закону электромагнитной индукции. Он показал, что всякий раз, когда проис­ходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электро­магнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электро­магнитной индукции 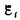определяются только скоростью изменения магнитного потока, т. е.

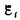
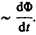
Теперь необходимо выяснить знак 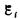. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта (см. § 109). Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к форм­улировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим кон­туром, возникающая в контуре э. д. с.

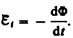(123.2)

Знак минус показывает, что увеличение потока вызывает э. д. с. 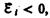т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока 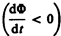вызывает 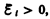т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) определяется правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызва­вшему этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона со­хранения энергии, как это впервые сделал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно перемещаться (см. рис. 177). Под действием силы Ампера F, направление которой показано на рисунке, проводник перемещается на отрезок d x. Таким образом, сила Ампера производит работу (см. (121.1)) d A = I dФ, где dФ — пересеченный проводником магнитный поток.

Согласно закону сохранения энергии, работа источника тока за время d t (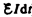) будет складываться из работы на джоулеву теплоту (I ² R d t) и работы по перемещению проводника в магнитном поле (I dФ):

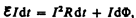
где R — полное сопротивление контура. Тогда

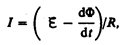
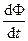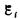= есть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадея можно сформулировать еще таким образом: э.д.с. 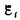электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э. д. с. 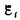не зависит от способа изменения магнитного потока. Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

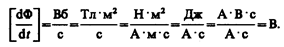
Какова природа э.д.с. электромагнитной индукции? Если проводник (подвижная перемычка контура на рис. 177) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводни­ком, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э.д.с. индукции при движения контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.

Согласно закону Фарадея, возникновение э.д.с. электромагнитной индукции воз­можно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора Е _B этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции:

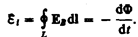(123.3)

§ 124. Вращение рамки в магнитном поле

Явление электромагнитной индукции применяется для преобразования механической энергии в энергию электрического тока. Для этой цели используются генераторы, принцип действия которых можно рассмотреть на примере плоской рамки, враща­ющейся в однородном магнитном поле (рис. 180).

Предположим, что рамка вращается в однородном магнитном поле (B=const)равномерно с угловой скоростью w=const. Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени t, согласно (120.1), равен

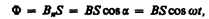
где a = wt — угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t =0 было a =0).

При вращении рамки в ней будет возникать переменная э.д.с. индукции (см. (123.2))

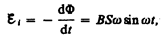(124.1)

изменяющаяся со временем по гармоническому закону. При sin wt = l э.д.с. 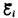мак­симальна, т. е.

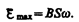(124.2)

Учитывая (124.2), выражение (124.1) можно записать в виде

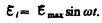
Таким образом, если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная э.д.с., изменяющаяся по гармоническому закону.

Из формулы (124.2) вытекает, что 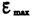(следовательно, и э.д.с. индукции) находится в прямой зависимости от величин w, B и S. В России принята стандартная частота тока n = w /(2p) = 50 Гц, поэтому возможно лишь увеличение двух остальных величии. Для увеличения В применяют мощные постоянные магниты или в электромагнитах пропу­скают значительный ток, а также внутрь электромагнита помещают сердечники из материалов с большой магнитной проницаемостью m. Если вращать не один, а ряд витков, соединенных последовательно, то тем самым увеличивается S. Переменное напряжение снимается с вращающегося витка с помощью щеток, схематически изображенных на рис. 180.

Процесс превращения механической энергии в электрическую обратим. Если по рамке, помещенной в магнитное доле, пропускать электрический ток, то в соответствии с (109.1) на нее будет действовать вращающий момент и рамка начнет вращаться. На этом принципе основана работа электродвигателей, предназначенных для превращения электрической энергии в механическую.

§ 125. Вихревые токи (токи Фуко)

Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказыва­ются замкнутыми в толще проводника и поэтому называются вихревыми. Их также называют токами Фуко — по имени первого исследователя.

Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать измене­нию магнитного потока, индуцирующему вихревые токи. Например, если между полюсами невключенного электромагнита массивный медный маятник совершает пра­ктически незатухающие колебания (рис. 181), то при включении тока он испытывает сильное торможение и очень быстро останавливается. Это объясняется тем, что возникшие токи Фуко имеют такое направление, что действующие на них со стороны магнитного поля силы тормозят движение маятника. Этот факт используется для успокоения (демпфирования) подвижных частей различных приборов. Если в описан­ном маятнике сделать радиальные вырезы, то вихревые токи ослабляются и торможе­ние почти отсутствует.

Дата добавления: 2014-11-25