Напряженное состояние и прочность материалов

При определении механических свойств строительных материалов используют законы сопротивления материалов – науки о прочности и деформативности материалов и конструкций.

Напряжение. Внешние силы, действующие на материальное тело, стремятся деформировать его. В ответ на их действие в материале воз­никают внутренние силы, препятствующие деформации материала, в результате чего вся система остается в равновесии. Мерой этих внут­ренних сил служит напряжение – сила, приходящаяся на единицу поверхности сечения материала (Н/м²).

Обычно напряжение р в точке М (рис. 4.8) представляют в виде двух состав­ляющих: нормального σ (перпендикуляр­ного плоскости сечения) и касательного τ напряжений, являющихся основными ха­рактеристиками напряженного состояния тела. В зависимости от соотношения и направления этих напряжений различают несколько видов напряженного состояния: сжатие, растяжение, изгиб, сдвиг и кру­чение.

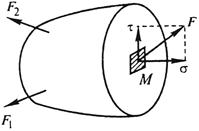
Рис. 4.8. Определение нормальных σ
и касательных τ напряжений в точке М

Деформация. Деформация – изменение относительного располо­жения частиц тела, вызванное их перемещениями под действием внешних сил. Деформация является результатом изменения меж­атомных расстояний (упругие деформации) и перегруппировки блоков атомов и молекул (пластические деформации). Упругие деформа­ции после снятия нагрузки исчезают, т.е. тело принимает свои ис­ходные размеры и форму. Пластические деформации сохраняются после снятия нагрузки – это необратимые деформации. Реальные тела в той или иной степени проявляют и упругие, и пластические деформации.

Основные виды деформаций тела в целом: растяжение, сжатие, изгиб, сдвиг, кручение и другие. Все многообразие деформаций представ­ляет собой сочетание простейших деформаций: растяжения (или сжа­тия) и сдвига.

За характеристику деформации принимают относительное удлине­ние (или укорочение) некоторого элемента тела:

ε = (l ₁ – l)/ l,

где l – первоначальная длина элемента, мм; l ₁ – длина элемента после де­формации, мм.

Модуль упругости. Между напряжением и деформацией упругих материалов существует прямая пропорциональная зависимость σ = Е ε, известная под названием закона Гука. Коэффициент пропор­циональности Е, характеризующий способность материала сопротив­ляться деформациям, называют модулем упругости (или модулем Юнга). Для различных материалов модуль упругости различен. Чем ниже модуль упругости, тем легче деформируется материал (например, модуль упругости стали 2·10⁵, бетона 3·10⁴, а резины около 10 МПа).

Основной конструктивный элемент, рассматриваемый в сопротив­лении материалов, – брус – тело, длина которого значительно боль­ше, чем высота и ширина. В зависимости от направления сил, дей­ствующих на брус, его называют стержнем или балкой.

Сжатие и растяжение. Если действующие силы направлены вдоль оси стержня (осевое сжатие или растяжение), то в нем возникают нормальные напряжения, одинаковые по всему поперечному сечению стержня. Значение напряжений σ (МПа) в этом случае рассчитывают по формуле

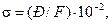(4.11)

где Р – сила, приложенная к стержню, Н; F – площадь поперечного сечения стержня, см².

Относительная деформация ε стержня при данном значении на­пряжения определяется как

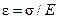, (4.12)

где Е – модуль упругости материала стержня, МПа.

При испытаниях строительных материалов на сжатие вместо стержня обычно применяют образцы-кубы и реже цилиндры. Расчет­ные формулы для куба такие же, как и для стержня.

Изгиб. При изгибе ось балки (рис. 4.9, a), которая была до воз­действия нагрузки прямолинейной, под действием этой нагрузки ис­кривляется. Причина искривления балки – изгибающий момент, действующий на нее. Чтобы определить момент, действующий на балку в любой ее точке, нужно мысленно рассечь балку в этой точке, отбросить одну ее половину и сосчитать сумму моментов всех внешних сил относительно этой точки (включая и реакцию опор). Сумма моментов даст зна­чение момента внутренних сил в балке в рассматриваемой точке.

На рис. 4.9, б пока­зана эпюра (график изменения) изгибаю­щего момента по длине балки для случая с одной сосредоточенной силой в центре. Максимальный изгибающий момент М_И (Н·м) в центре балки определяется как

М_И = Рl /4, (4.13)

где Р – сила, приложенная к балке, Н; l – расстояние между опорами, м.

Для других случаев нагружения и опирания балки изгибающий момент рассчитывают по другим формулам.

Изгибающий момент вызывает прогиб балки, причем при рас­сматриваемой схеме нагружения балка со стороны нагрузки будет вогнутой, а с противоположной стороны – выпуклой (рис. 4.9, в). В этом случае напряжения, связанные с деформациями законом Гука (4.12), неодинаковы по

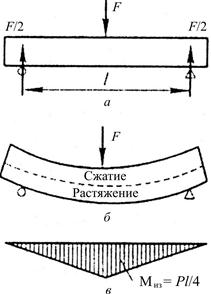
Рис. 4.9. Схемы нагружения (а) и деформации
моментов (в); эпюра изгибающих моментов (б)

высоте сечения. Поэтому при оп­ределении напряжений в материале необходимо учитывать не только площадь его сечения, как при сжатии и растяжении, но и распределе­ние материала по высоте сечения. Примером может служить различное сопротивление нагрузке доски, поставленной на ребро и лежащей.

Характеристику поперечного сечения, учитывающую распреде­ление материала по высоте сечения, называют моментом сопротив­ления сечения W. Для прямоугольного сечения момент сопротивле­ния определяется по формуле

W = bh ² /6,

где b – ширина балки, м; h – высота балки, м.

Максимальные напряжения, возникающие в крайних (верхнем и нижнем) волокнах для рассматриваемого случая нагружения балки прямоугольного сечения, определяется как

.

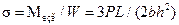Наиболее выгодными при изгибе оказываются балки с попереч­ным сечением, при котором основная масса материала расположена по краям элемента (например, двутаврового сечения).

Сдвиг. Сдвиг (срез) можно наблюдать, когда, например, материал режут ножницами. В этом случае к двум смежным сечениям при­ложены противоположные по направлению силы. В области действия этих сил возникает напряженное состояние сдвига, характеризуемое касательными напряжениями 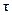, которые вычисляют по формуле

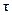= P / F, (4.14)

где F – сечение бруса вдоль линии действия силы, м².

Предел прочности материала. При определении прочности строительных материалов образец материала доводят до разрушения. На рис. 4.10, а, б представлены диа­граммы испытания на растяже­ние хрупкого и пластичного ма­териалов до стадии их разруше­ния. Задача таких испытаний – определение напряжения, ниже которого материал существует неограниченно долго, а выше которого – разрушается мгно­венно. Это предельное напря­жение называется пределом прочности материала и обозна­чается R. Предел прочности рас­считывают по тем же формулам, что и напряжения, но вместо действующей силы берут силу разру­шающую P _p.

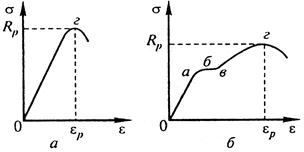
Рис. 4.10. Диаграмма деформации–напряжения
при испытании на растяжение хрупких (а)
и упругопластичных (б) материалов
(σ – напряжение, ε – относительная деформация)

Предел прочности – основная характеристика механических свойств материала; чаще всего определяют предел прочности при сжатии R _сж и при изгибе R _и.

Дата добавления: 2014-11-25