Краткая теория. Вязкость жидкости– это свойство, характеризующее возникновение сил внутреннего трения при относительном скольжении слоев жидкости

Вязкость жидкости – это свойство, характеризующее возникновение сил внутреннего трения при относительном скольжении слоев жидкости, движущихся с различными скоростями, причем сила направлена по касательной к поверхности соприкосновения слоев.

При движении жидкости между её слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоёв.

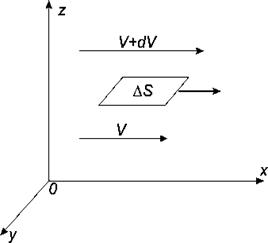
Рис. 1.

Движение жидкости

Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами, что приводит к перераспределению импульсов слоев жидкости. Молекулы из более быстрого слоя передают молекулам более медленного слоя часть импульса, вследствие чего медленный слой начинается двигаться быстрее, а быстрый слой тормозится.

Рассмотрим жидкость, движущуюся в направлении х (рис. 1). Пусть слои жидкости движутся с разными скоростями. На оси 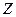возьмем две точки, находящиеся на расстоянии 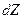. Скорости потока жидкости отличаются в этих точках на величину 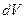. Отношение 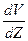характеризует изменение скорости потока в направлении перпендикулярном направлению скоростей и называется градиентом скорости. При ламинарном течении (т.е. без завихрений) сила внутреннего трения (или вязкости), действующая между слоями, пропорциональна площади их соприкосновения 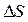и градиенту скорости (формула Ньютона):

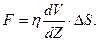
(15)

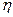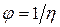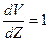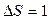Величина называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Величина называется текучестью. Если в формуле (1) принять и , то 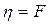, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом скорости, равным единице. Наряду с коэффициентом динамической вязкости 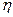, часто употребляют коэффициент кинематической вязкости 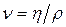, где 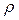– плотность жидкости. В системе СИ единицей физических величин измерений динамической вязкости 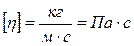; кинематической вязкости .

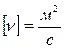Коэффициент динамической вязкости 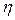зависит от природы жидкости и для данной жидкости с повышением температуры уменьшается. Слой жидкости, непосредственно прилегающий к твердой поверхности, в результате прилипания остается неподвижным относительно её. Скорость остальных слоев постепенно возрастает по мере удаления от твердой поверхности.

Определение коэффициента вязкости жидкости по методу Стокса:

На всякое тело, движущееся в вязкой жидкости, действует сила сопротивления. В общем случае величина этой силы зависит от многих факторов: от внутреннего трения жидкости, от формы тела, от характера обтекания и т.д. Стоксом было получено строгое решение задачи о ламинарном обтекании шарика безграничной жидкостью. В этом случае сила сопротивления 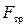определяется формулой:

,

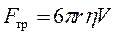(2)

где 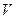- скорость шарика, 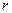- радиус шарика, 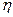- коэффициент динамической вязкости жидкости.

Рассмотрим падение шарика в вязкой среде (рис. 1). На шарик действуют три силы:

1. сила тяжести 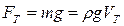(ρ – плотность материала шарика,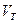 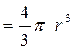– объем шарика);

2. сила Архимеда 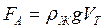, равная весу жидкости в объеме 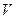( 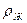‑плотность жидкости);

3. сила сопротивления со стороны жидкости (сила Стокса) .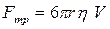

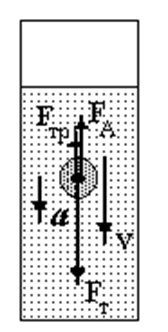
Рис. 2.

Движение шарика в вязкой жидкости

Равнодействующая этих сил обеспечивает шарику, согласно второму закону Ньютона, ускорение:

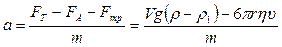
(3)

Таким образом, скорость шарика υ с течением времени растет, а следовательно, растет и сила сопротивления 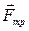со стороны жидкости, пропорциональная модулю скорости. Когда 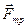возрастет настолько, что сумма сил 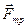и 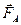уравновесит силу тяжести 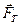, движение шарика станет равномерным (a = 0), т.е. с постоянной скоростью 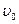= const.

Измеряя на опыте установившуюся скорость падения шарика 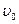и радиус шарика 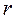, зная значения плотностей материала шарика 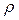и жидкости 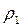, в которой он движется, можно определить коэффициент внутреннего трения (коэффициент вязкости) жидкости по формуле:

.

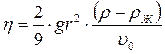(4)

Дата добавления: 2014-11-25