Пара сил. Момент пары

Cистема двух равных по модулю параллельных друг другу и направленных в разные стороны сил 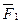и , линии действия которых не совпадают (рисунок 1.10), образует так называемую пару сил, или просто пару, для обозначения которой будем пользоваться символом .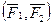

Плоскость, в которой расположена пара сил, называется плоскостью действия пары.

Кратчайшее расстояние между линиями действия сил пары 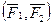, т. е. длина перпендикуляра, опущенного из точки приложения А одной из сил пары на линию действия второй силы, называется плечом пары d.

Пара сил не имеет равнодействующей, т.е. ее нельзя заменить одной силой, ей эквивалентной. Поэтому пара сил не может быть уравновешена одной силой. Вместе с тем силы, составляющие пару сил, не находятся в равновесии.

Вращательное действие пары на тело будет тем больше, чем больше плечо пары и модули сил, образующих эту пару, и измеряется так называемым моментом пары. При этом численное значение момента пары определяется как произведение модуля одной из сил пары на плечо этой пары.

Алгебраическим моментом пары называется скалярная величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо. Будем обозначать момент пары символом m или m 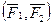. Тогда

.

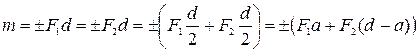(1.19)

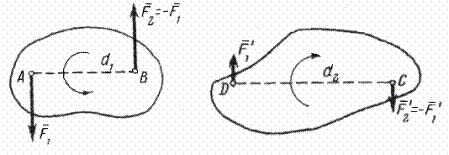
Рисунок 1.10 – Пары сил

Очевидно, что момент пары равен моменту одной из ее сил относительно точки приложения другой.

Понятие момента пары не следует смешивать с моментом силы. Понятие момента силы связано с точкой, относительно которой берется этот момент. Момент пары ни с какой точкой плоскости не связан.

Теорема: Действие пары на тело не изменится, если эту пару заменить любой другой парой, лежащей в той же плоскости и имеющей тот же момент.

Из данной теоремы вытекают следующие свойства пары сил:

1. Действие пары на тело не изменяется, если переместить пару в другое положение в плоскости ее действия.

(Заметим, что перенос пары в ее плоскости действия, так же как и перенос точки приложения силы вдоль линии ее действия, безоговорочно применим только для абсолютно твердого тела).

2. Действие пары на тело не изменится, если одновременно изменить модуль сил пары и величину ее плеча, сохраняя при этом численное значение и знак момента пары.

Всякую систему пар, расположенных в одной плоскости, можно заменить одной равнодействующей парой, момент которой равен алгебраической сумме моментов всех пар этой системы.

Для равновесия системы пар, расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма моментов всех данных пар равнялась нулю, т. е.

.

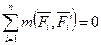(1.20)

Теорема о параллельном переносе силы. (Метод Пуансо)

Докажем следующую теорему: Действие силы на твердое тело не изменяется, если ее перенести параллельно самой себе в любую другую точку этого тела, приложив при этом пару с моментом, равным моменту переносимой силы относительно той точки, в которую переносится сила.

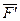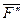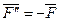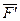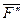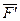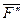Пусть на твердое тело действует сила , приложенная в точке А (рисунок 1.21, а). Действие этой силы на точку не изменяется, если в произвольной точке В тела приложить две уравновешенные силы и , такие, что , . Полученная система трех сил , , (рисунок 1.21, б) эквивалентно одной заданной силе . При этом система сил , , представляет собой силу, но приложенную в точке В, и пару с моментом 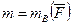, так как момент пары равен моменту одной из ее сил относительно точки приложения другой.

Рисунок 1.21 – Параллельный перенос силы

Таким образом, теорема доказана. Если условиться пару изображать круглой стрелкой, то результат, даваемый этой теоремой, можно изобразить так, как показано на рисунке 1.21, в.

Доказанная теорема о параллельном переносе силы кладется в основу при решении задачи о приведении произвольной плоской системы сил к простейшей ей эквивалентной системе.

Дата добавления: 2014-11-25