Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил

Аксиомы статики.

1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁=F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 1.2).

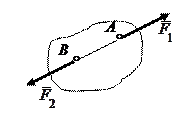
Рисунок 1.2 – Равновесие абсолютно твёрдого тела под действием двух сил

Иными словами это означает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.

Следствие: действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.

В самом деле, пусть на твердое тело действует приложенная в точке А сила 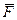(рис. 1.3). Возьмем на линии действия этой силы произвольную точку В и приложим в ней две уравновешенные силы 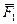и 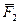, такие, что 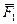= 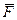и 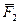= . От этого действие силы 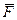натело не изменится. Но силы 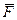и 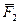также образуют уравновешенную систему, которая может быть отброшена. В результате на тело будет действовать только одна сила 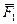,равная 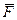,но приложенная в точке В. (Отброшенные или перенесенные силы будем на рисунках перечеркивать.)

Таким образом, вектор, изображающий силу 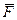, можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).

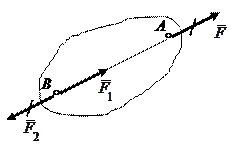
Рисунок 1.3 – Перенос силы вдоль линии действия

Полученный результат справедлив только для сил, действующих на абсолютно твердое тело. При инженерных расчетах им можно пользоваться лишь тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникшие в ее частях внутренние усилия.

Например, изображенный на рис. 1.4, а стержень АВ будет находиться в равновесии, если F ₁= F ₂. При переносе точек приложения обеих сил в какую-нибудь точку С стержня (рис. 1.4, б) или при переносе точки приложения силы 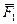в точку В, а силы 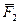в точку А (рис. 1.4, в) равновесие не нарушается. Однако внутренние усилия будут в каждом из рассматриваемых случаев разными. В первом случае стержень под действием приложенных сил растягивается, во втором случае он не напряжен, а в третьем – стержень будет сжат.

Рисунок 1.4 – Изменение внутренних усилий при переносе точек приложения сил

Следовательно, при определении внутренних усилий переносить точку приложения силы вдоль линии действия нельзя.

Закон равенства действия и противодействия: при всяком действии одного материального тела на другое имеет место такое же численно, но противоположное по направлению противодействие.

Эта аксиома проиллюстрирована рисунком 1.7. Если тело А действует на тело В с силой 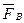, то одновременно тело В действует на тело А с силой . Нужно запомнить, что силы 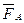и 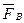не образуют уравновешенной системы сил, так как они приложены не к одному, а к двум разным телам. Из этой аксиомы следует, что в природе не существует одностороннего действия силы.

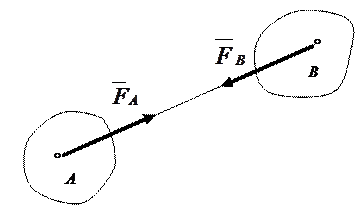
Рисунок 1.7 - Закон равенства действия и противодействия

Свойство внутренних сил. Любые две части тела (или конструкции) действуют друг на друга с равными по модулю и противоположно направленными силами. Так как при изучении условий равновесия тело рассматривается как абсолютно твёрдое, то все внутренние силы образуют при этом уравновешенную систему сил, которую можно отбросить. Следовательно, при изучении условий равновесия тела (конструкции) необходимо учитывать только внешние силы, действующие на это тело (конструкцию). В дальнейшем, говоря о действующих силах, мы будем подразумевать, если не сделано специальной оговорки, что речь идёт только о внешних силах.

Принцип отвердевания. Если деформируемое тело находится под действием некоторой системы сил в равновесии, то равновесие не нарушится и в том случае, если это тело отвердеет (станет абсолютно твердым).

Из принципа отвердевания следует, что условия равновесия, являющиеся необходимыми и достаточными для абсолютно твердого тела, являются необходимыми, но недостаточными для соответствующего деформируемого тела.

Например, твердый брусок (рисунок 1.8, а, б) находится в равновесии под действием двух сил, равных по модулю и направленных вдоль оси бруска друг к другу либо друг от друга, а нить, соответствующая этому бруску, находится в равновесии только под действием двух сил, равных по модулю и направленных вдоль нити друг от друга (рисунок 1.9). Очевидно, что под действием сил, направленных друг к другу, нить сомнется.

Рисунок 1.8 – Равновесие жёсткого стержня при растяжении (а), и сжатии (б)

Рисунок 1.9 – Равновесие нити при растяжении

Закон параллелограмма сил: две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.

Вектор 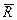, равный диагонали параллелограмма, построенного на векторах 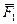и 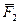(рис. 1.5), называется геометрической суммой векторов F ₁ и F ₂:

.

(1.2)

Следовательно, закон параллелограмма сил можно еще сформулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

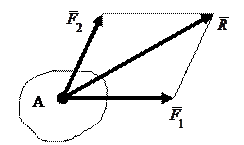
Рисунок 1.5 – Параллелограмм сил

В дальнейшем следует различать понятия суммы сил и их равнодействующей. Поясним это примером. Рассмотрим две силы 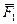и 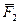(рис. 1.6), приложенные к телу в точках А и В. Показанная на рис. 1.6 сила равна геометрической сумме сил 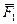и 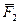(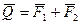), как диагональ соответствующего параллелограмма. Но сила не является равнодействующей этих сил, так как нетрудно понять, что одна сила не может заменить действие сил 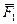и 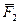на данное тело, где бы она ни была приложена. В дальнейшем будет ещё строго доказано, что эти две силы не имеют равнодействующей.

Рисунок 1.6 – Случай, когда сумма сил не является равнодействующей

Дата добавления: 2014-11-25