Структурные средние. Для характеристики состава изучаемой совокупности пользуютсяструктурными величинами

Для характеристики состава изучаемой совокупности пользуются структурными величинами. Они бывают двух видов:

· Мода –наиболее часто встречающееся значение ряда (варианты). Мода применяется, например, при определении размера обуви, одежды, пользующейся наибольшим спросом у покупателей.

Для дискретных рядов мода – это вариант, имеющий наибольшую частоту.

При расчете моды для интервального ряда необходимо вначале определить модальный интервал, т.е. интервал, который имеет наибольшую частоту, а затем значение модального признака. В этом случае моду рассчитывают по следующей формуле:

х_мо – нижняя граница модального интервала;

i_мо - величина модального интервала;

f_мо – частота, соответствующая модальному интервалу;

f_мо-1 – частота, предшествующая модальному интервалу;

f_мо+1 – частота интервала, следующего за модальным.

Мода определяет непосредственно размер признака, свойственный, хотя и значительной части, но все же не всей совокупности. Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующей совокупность в целом с учетом всех без исключения элементов совокупности.

J производительность труда (руб) число рабочих

10-15 5

15-20 12

20-25 19

25-30 11

св. 30 8

Модальный интервал: 20-25

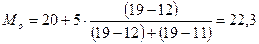
· Медиана – значение признака, которое делит численность ранжированного ряда на две равные части.

Для ранжированного ряда с нечетным числом единиц медианой будет являться вариант, расположенный в центре ряда. (J 4, 6, 7, 9, 11, 12. Медиана =7)

Для ранжированного ряда с четным числом единиц медиана определяется как среднее арифметическое из двух смежных вариант, находящихся в центре ряда. (J 4, 6, 8, 9,, 12, 13. Медиана=8,5)

В интервальных рядах для определения медианы необходимо:

1.расположить значение признака по ранжиру;

2.для ранжированного ряда определить сумму накопленных частот;

3.найти медианный интервал. Он будет находиться там, где полусумма накопленных частот больше или равна сумме частот. Медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот;

Значение медианы находится по формуле:

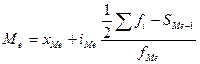
х_ме – нижняя граница медианного интервала;

i_ме – величина медианного интервала;

f /2 – полусумма частот ряда;

S_ме-1 – сумма накопленных частот, предшествующих медианному интервалу;

f_ме – частота медианного интервала.

J тот же пример, что и для расчета моды

Сумма накопленных частот

Медианный интервал:20-25 (совпал с модальным)

Полусумма накопленных частот=55/2=27,5

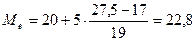
Медиана не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда, поэтому ее применение позволяет получить более точные результаты, чем при использовании других форм средних.

Тема 5. Показатели вариации и анализ частотных распределений

Дата добавления: 2014-11-25