I. Однофакторный дисперсионный анализ

Дисперсионный анализ

1.1. F -критерий как мера сравнения статистических показателей нескольких выборок

В ходе практической деятельности часто при оценке качества продукции интересуются только одним (важнейшим в конкретной ситуации) показателем качества. Обозначим этот показатель через X.

Предположим, что интересующая продукция может поступать к потребителю по различным каналам, например, от различных поставщиков, а в качестве показателя качества выступают числовые значения (x ₁, x ₂,…, x _k и т.д.) некоторого параметра (или характеристики) продукции. Из имеющегося множества каналов поставки следует выбрать наилучший канал, или, иными словами, выбрать лучшего поставщика. Для сравнения качества продукции, поступаемой от r поставщиков, проводятся ее выборочные испытания, по результатам которых вычисляются средние арифметические значения 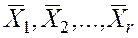и принимаются заключения о соответствующих им значениях математических ожиданий µ ₁, µ ₂,…, µ _r. Последние величины уже не случайны, т.к. они характеризуют качество продукции каждого из поставщиков в целом, а не качество отдельных случайных выборок.

В связи с тем, что значения показателей качества X, также как и их выборочные и средние арифметические значения, являются случайными величинами, распределенными в некотором диапазоне значений, который теоретически безграничен, то, в каждом конкретном случае, необходимо установить приемлемый диапазон значений, который бы был достоверной оценкой качества поставляемой продукции. Еще раз отметим, что качество продукции оценивается по некоторому целевому значению, роль которого в проводимых экспериментальных исследованиях выполняют средние арифметические значения 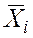результатов испытаний продукции каждого поставщика. Различие между всеми средними 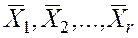всегда существует, но является ли оно значимым, или между какими-то группами оно значимо, а между другими группами, при выдвинутых требованиях к качеству рассматриваемого вида продукции, оно неразличимо.

Научно обоснованный ответ на поставленные вопросы часто делают на основе методологии дисперсионного анализа (ДА), в основе которой лежит одно из фундаментальных положений КАЧЕСТВА – вариации собственных характеристик продукции ухудшают ее качество.

В дисперсионном анализе (Analysis of Variance - ANOVA)[1] сравнение матема­тических ожиданий для показателей качества продукции различных поставщиков осуществляется именно на основе анализа вариации данных.

Предположим, что из группы r поставщиков однородной продукцииследует установить лучших. Каждый из r поставщиков представляет на испытания п₁, п₂,..., п_r единиц продукции соответственно.Общее количество продукции, представленной на испытания равно п = п₁ + п₂+... + п_r. Предположим далее, что все п единиц продукции извлечены из независимых генеральных совокупностей, каждая из которых имеет нормальное распределение и одинаковую дисперсию. По результатам испытаний сформулируем статистические гипотезы.

Нулевая гипотеза заклю­чается в том, что математические ожидания генеральных совокупностей одинаковы:

H ₀: μ ₁= μ ₂ =…= μ _r [2].

Если графически изобразить плотности вероятностей этих распределений, то они накладываются одна на другую, имея одинаковые математическое ожидание, вариа­цию и форму.

Альтернативная гипотеза гласит, что не все математические ожидания одинаковы.

H ₁: не все μ _j одинаковы (j =1. 2,..., r).

Графически эта ситуация (для случая r = 3) изображена на рис.1.

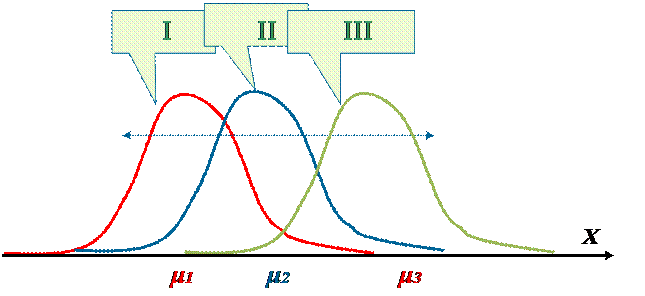Рис. 1. Плотности вероятностей нормально распределенных случайных величин с равными дисперсиями и различными математическими ожиданиями

При проверке гипотезы о равенстве математических ожиданий нескольких гене­ральных совокупностей полная вариация разделяется на две части (рис. 2): межгрупповую ва­риацию, обусловленную разностями между группами, и внутригрупповую, обуслов­ленную разностями между элементами, принадлежащими одной группе. Поскольку нулевая гипотеза заключается в том, что математические ожидания всех r групп равны между собой, полная вариация равна сумме квадратов разностей между отдельными наблюдениями и общим средним 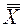, вычисленным по всем выборочным значениям:

Составляющие полной вариации фактора в группах
Полная вариация, V S Число степеней свободы df = n- 1		Межгрупповая вариация, V мг Число степеней свободы df мг = r- 1
Внутригрупповая вариация, V вг Число степеней свободы df вг = n- r

Рис. 2.Составляющие полной вариации фактора в группах

- полная вариация,(1)

где 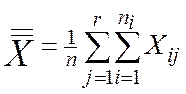- общее среднее,

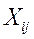— i - енаблюдение в j -й группе,

п_j — количество наблюдений в j -й группе,

п — общее количество наблюдений во всех группах (т.е. п = п₁ + п₂+... + п_r),

r - количество изучаемых групп.

Межгрупповая вариация, называемая обычно межгрупповой суммой квадратов, равна сумме квадратов разностей между выбо­рочным средним каждой группы 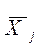,и общим средним 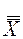, умноженных на объем соответствующей группы п _j:

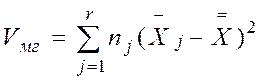. (2)

Внутригрупповая вариация, называемая обычно внутригрупповой суммой квадра­тов, равна сумме квадратов разностей между элементами каждой группы и выборочным средним этой группы :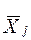

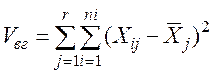(3)

Поскольку сравнению подвергаются r уровней фактора, межгрупповая сумма квад­ратов имеет r -1 степеней свободы. Каждый из r уровней обладает п _j - 1степенями свобо­ды, поэтому внутригрупповая сумма квадратов имеет п – r степеней свободы:

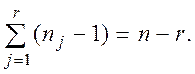
Кроме того, общая сумма квадратов имеет n - 1 степеней свободы, поскольку каждое на­блюдение X _ij сравнивается с общим средним 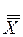, вычисленным по всем п наблюдениям.

Если каждую из этих сумм разделить на соответствующее количество степеней сво­боды, получим три вида дисперсий D – средних значений сумм квадратов (mean square – MS):

межгрупповая дисперсия ;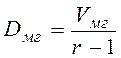

внутригрупповая дисперсия

и полная дисперсия .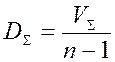

Следует еще раз подчеркнуть, что основное предназначение дисперсионного анализа — сравнить математические ожидания r групп. А главным инструментом для выявления возможных различий между математическими ожиданиями r выступает дисперсионный анализ -анализ дисперсий между группами и внутри каждой группы. Критерий принятия или отклонения нулевой гипотезы базируется на распределении Фишера-Снедекора (F -распределении). В рассматриваемом примере дисперсионного анализа F - статистика представляет собой отношение двух дисперсий - D_{м г} и D_вг:

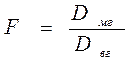. (4)

При заданном уровне значи­мости α нулевая гипотеза отклоняется, если вычисленная F -статистика больше верхнего критического значения F _кр [3],присущего F -распределению с r -1 степенями свободы в числи­теле и n-r степенями свободы в знаменателе.

Если нулевая гипотеза H ₀ является истинной, то смещение между группами близко к нулю, а рассчитанная по формуле (4) F -статистика близка к 1, поскольку ее числитель и знаменатель являются оценками одной и той же дисперсии. Если нулевая гипотеза H ₀ является ложной (и между математическими ожиданиями разных групп существует значительная разница), то вычисленная F -статистика будет намного больше единицы, поскольку ее чис­литель содержит вариации данных внутри группы и вариации между группами, а знаменатель оценивает лишь внутригрупповую вариацию.

Для иллюстрации методики проведения однофакторного дисперсионного анализа рассмотрим конкретный пример планирования и проведения эксперимента.

Упражнение 1.

В сеть магазинов «Охота и Рыбалка» свою продукцию предлагают производители лески для рыбной ловли. Одним из основных показателей качества лески является предельное усилие, при котором происходит ее разрыв. Производители рыболовной лески перед заключением договоров на поставку своей продукции в сеть магазинов «Охота и Рыбалка», рекламирует прочность лески, и с этой целью проводят ее испытания на разрыв.

Предположим, что, совершенствуя продукцию, изыскивая новые технологии производства, производитель освоил 4-е технологии производства рыболовной лески. Испытания на разрыв для каждого диаметра (толщины) лески производятся выборочно. Из партий продукции, производимой по различным технологиям, случайным образом выбирается по 5 образцов лески одного и того же диаметра и производятся их испытания на разрыв в идентичных условиях. Результаты испытаний лески на разрыв представлены в табл. 1.

Анализ полученных данных показывает, что между выборочными средними наблюдается неко­торая разница. Можно ли на­звать эту разницу статистически значимой (существенной)? Иными словами, полученные значения среднего арифметического по пяти выборкам дают ли нам право ранжировать технологии производства лески по критерию «ПРОЧНОСТЬ» в виде следующего ряда: 3, 2, 1 и 4 соответственно? Т.е., технология 3 обеспечивает наивысшую прочность лески, а технология 4 – наименьшую прочность.

Для ответа на поставленный вопрос сформулируем вначале основную и альтернативную гипотезы.

Нулевая гипотеза утверждает, что между средними показателями качества продукции (прочность рыболовной лески), изготовляемой по различным технологиям, нет существенных различий:

H ₀: μ₁= μ₂= μ₃= μ₄.

Альтернативная гипотеза заключается в том, что качество продукции (прочность рыболовной лески), изготовляемой по различным технологиям, имеет существенные различия:

Н ₁:не все μ _j одинаковы (j =1, 2, 3, 4).

Таблица 1

Исходная таблица для дисперсионного анализа

Результаты испытаний лески	Технология 1	Технология 2	Технология 3	Технология 4
Усилия, при которых происходит разрыв лески диаметром 0,35 мм, (кг)	34.5	29.5	33.5
29.5			28.5
31.5		30.5
	31.5
Среднее арифметическое,	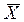31,5	30,4	32,8	29,5

Чтобы по исходным данным выполнить дисперсионной анализ, сначала необходимо вычислить выборочные средние для каждой группы, затем нужно найти общее среднее, просуммировав все 20 чисел и разделив их на общее количество наблю­дений.

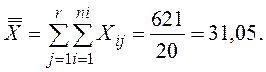
Затем определяют вариации:

межгрупповую, V_{м г}; внутригрупповую, V_{в г}; полную V_S.

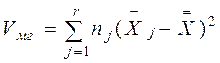= 5x(31,5 - 31,05)² + 5 x (30,4 - 31,05)² +

+5 x (32,8 - 31,05)² + 5 x (29,5 - 31,05)² = 30,45;

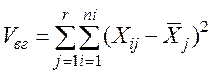= (34,5 – 31,5)² + … + (33 – 31,5)² + (29,5 – 30,4)² + … + (31,5 – 30,4)² + (33,5 – 32,8)² + … + (33 – 32,8)² + (29 – 29,5)² … (30 – 29,5)² = 45,5;

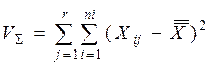= (34,5 - 31,05)² + (29 - 31,05)² +… + (30 - 31,05)² = 75,95.

Откуда получаем значения дисперсий D_мг и D_вг, а также F -статистику:

;

;

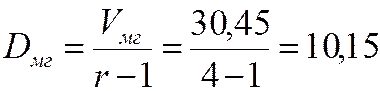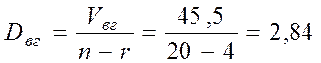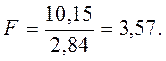
При заданном уровне значимости a верхнее критическое значение F _кр,для F - распределения, определяется по таблице Приложения 1 «Критические значения F -статистики при уровне значимости a = 0,05».

В данной задаче числитель имеет три степени свободы, а знаменатель — 16. Таким образом, при уровне значимости, равном 0,05, верхнее кри­тическое значение F _кр равно 3,24. Поскольку вычисленная F -статистика, равная 3,57, превышает верхнее критическое значение F _кр, нулевая гипотеза отклоняет­ся.

Следовательно, дисперсионный анализ экспериментальных данных, о прочности рыболовной лески показал, что среди четырех технологий изготовления лески не все из них обеспечивают одинаковую прочность лески. По крайней мере, по одной из технологий качество лески будет отличаться от продукции, изготавливаемой по другим технологиям.

Обнаружив существенные различия между математиче­скими ожиданиями анализируемых показателей качества продукции (в данном примере – прочности рыболовной лески), необходимо определить, какие именно технологии, среди рассматриваемых, обеспечивают наивысшее качество, а какие не различимы по качеству?

В методологии дисперсионного анализа существует несколько способов решения этой задачи, например,про­цедура множественных сравнений Тьюки - Крамера. Не будем рассматривать эту и другие процедуры, т.к. для рассматриваемого примера более просто выбрать лучшие варианты решений, методом простого перебора.

1.2. Процедуры Microsoft Excel: однофакторный дисперсионный анализ

Громоздкие вычисления дисперсионного анализа легко и просто выполнять с помощью программы Microsoft Excel «Однофакторный дисперсионный анализ».

Выполнение расчетов по методологии однофакторного дисперсионного анализа в Microsoft Excel имеет следующую последовательность.

1. В Excel необходимо создать рабочий лист, в столбцы которого внести исходные данные с результатами измерений продукции по каждому из ее поставщиков.

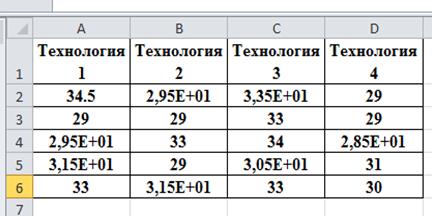
Примечание. В некоторых ячейках таблицы применена математическая форма представления чисел, так 2,95Е+01 = 29,5 = 295Е-1.

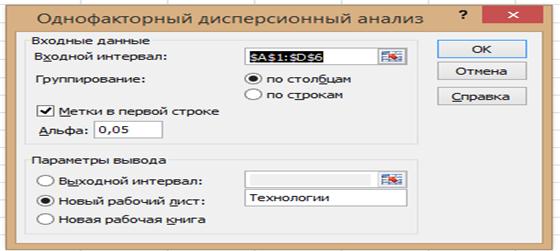
2. Последовательно выполнить команды: Данные => Анализ данных => Однофакторный дисперсионный анализ=> ОК.

3. В диалоговом окне Однофакторный дисперсионный анализ последовательно выполнить следующее:

* в окне Входной интервал обозначить номера ячеек, в которых содержатся сведения об анализируемой продукции (наименования продукции и результаты измерений);

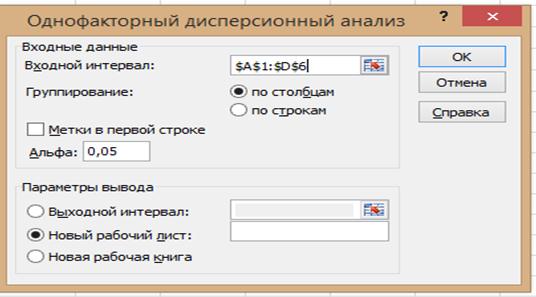
* в окне Группирование установить переключатель в положение: по столбцам;

* в окне Метки в первой строке установить значок Ú

* в окне Альфа число 0, 05 не изменять, если за доверительную вероятность нулевой гипотезы принято значение 0,95;

* в окне Параметры вывода установить переключатель в положение новый рабочий лист и ввести название «Технологии».

4. Нажать кнопку ОК.

В таб. 2 представлена итоговая таблица Microsoft Excel дисперсионного анализа для исходных данных, приведенных в табл. 1. Итоговые данные табл. 2 целиком и полностью совпадают с выполненными расчетами по определению F -статистики. Кроме того, в итоговой таблице дисперсионного анализа, полученной с помощью программы Microsoft Excel, приведено и Р – значение, которому соответствует число 0,038 - равное вероятности того, что при истинной нулевой гипотезе, F -статистика не будет превышать значения 3,57. Поскольку величина Р – значения не превышает уровень значимости α = 0,05, нулевая гипотеза отклоняется.

Р - значение позволяет, не пользуясь таблицами F -распределения, сделать непосредственный вывод об истинности нулевой гипотезы.

Если Р - значение меньше выбранного уровня значимости a, нулевая гипотеза отклоняется.

Таблица 2

Итоговая таблица дисперсионного анализа

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисп.
Технология 1		157.5	31.5	5.375
Технология 2			30.4	3.175
Технология 3			32.8	1.825
Технология 4		147.5	29.5
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-зн.	F кр.
Между группами	30.45		10.15	3.57	0.038	3.24
Внутри групп	45.5		2.84
Итого	75.95

Исключив из рассмотрения технологию 4, которая по результатам испытаний обеспечивает наименьшую прочность лески, и, выполнив с помощью программы Microsoft Excel дисперсионный анализ для оставшихся 3-х технологий, получим итоговые данные (см. табл. 3), которые не дают нам веских оснований для отклонения нулевой гипотезы.

Таким образом, можно констатировать, что прочность рыболовной лески, изготовляемой по технологиям 1, 2 и 3 – статистически (на уровне значимости α = 0,05) не различима.

Таблица 3

Таблица дисперсионного анализа для оценки качества лески, производимой по 1-й, 2-й и 3-й технологиям

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисп.
Технология 1		157.5	31.5	5.375
Технология 2			30.4	3.175
Технология 3			32.8	1.825
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-зн.	F кр.
Между группами	14.43		7.22	2.09	0.167	3.88
Внутри групп	41.5		3.46
Итого	55.93

С целью иллюстрации реальных трудностей, возникающих при оценке качества продукции, в табл. 4 приведены данные компьютерного моделирования 10 поставщиков продукции, показатель качества которой распределен по нормальному закону, имеет равные σ = 1 и различные математические ожиданиями µ _i (i =1, 2,..., 10). Для оценки реальных значений µ от каждого поставщика выбрано для испытаний по 10 единиц продукции. Анализ полученных данных показывает, что продукция не всех поставщиков различима по качеству. В частности, статистически не различима по качеству продукция от 2-го, 3-го и 4-го поставщика (см. табл. 5).

Таблица 4

Выборочные значения из 10-и нормально распределенных генеральных совокупностей (ГС) с одинаковыми значениями σ = 1 и различными математическими ожиданиями µ; объем выборки из каждой ГС n = 10

-0.723	-0.205	1.107	0.444	1.800	-0.586	3.149	2.282	3.599	4.956
-0.117	-0.037	2.441	-0.331	2.579	0.143	3.621	1.662	2.892	4.461
-2.160	-0.532	-0.094	-0.395	0.291	0.608	2.566	3.431	2.180	4.822
-1.394	1.603	-0.119	-0.179	0.767	2.224	2.440	3.272	3.047	6.618
0.659	-0.499	1.478	-0.927	0.191	1.556	3.292	2.753	2.264	4.218
-0.877	-1.65	0.556	1.745	2.538	2.782	2.852	1.133	3.396	5.466
-1.517	-0.096	0.150	2.461	1.502	2.937	0.874	1.870	3.444	5.656
-0.852	-0.434	-0.134	0.059	-0.304	1.675	0.737	3.808	2.644	6.226
-1.640	1.392	1.874	0.202	2.420	1.266	2.468	3.039	3.723	6.060
-2.003	-0.178	1.270	0.820	1.608	0.958	3.164	3.729	3.110	7.186
µ = -1	µ = -0,5	µ = 0	µ =0,5	µ = 1	µ =1,5	µ =2	µ =2,5	µ =3	µ =5
Выборочное среднее,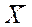
-1,06	-0,06	0,853	0,39	1,33	1,36	2,52	2,70	3,02	5,57
Стандартное отклонение, S
0,87	0,94	0,92	1,03	1,11	1,18	0,98	0,92	0,54	0,97

Таблица 5

Сводная таблица дисперсионного анализа для оценки качества продукции 2-го, 3-го и 4-го поставщиков

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Столбец 2		-0.636	-0.0636	0.888
Столбец 3		8.529	0.8529	0.843
Столбец 4		3.899	0.3899	1.072
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Знач.	F крит.
Между группами	4.20		2.10	2.25	0.125	3.35
Внутри групп	25.237		0.935
Итого	29.437

Ограничения, налагаемые на применение однофакторного дисперсионного анализа

Однофакторный ДА можно применять, только если выполня­ются следующие условия:

* экспериментальные данные случай­ны и независимы;

* экспериментальные данные - это выборки из нормально распределенных генеральных совокупностей;

* дисперсии экспериментальных данных для каждой группы равны между собой

Первое условие — случайность и независимость данных — должно выпол­няться всегда. Нарушение этого условия может серьезно исказить результаты дисперсионного анализа.

Второе предположение — нормальность — означает, что данные извлечены из нор­мально распределенных генеральных совокупностей. Вместе с этим, однофакторный дисперсионный анализ на основе F -критерия не чувствителен к на­рушению этого условия, если распределения не слишком значительно отличаются от нор­мальных законов, имеют симметричную форму, а объемы выборок достаточно велики.

Третье предположение — однородность дисперсии — означает, что дисперсии каж­дой генеральной совокупности должны быть равны между собой. Если объемы групп совпадают, условие однородности дисперсии слабо влияет на выводы, по­лученные с помощью F -критерия. Однако если объемы выборок различаются между собой, нару­шение условия о равенстве дисперсий может исказить результаты дисперси­онного анализа. Таким образом, чтобы не проводить дополнительных исследований по оценке однородности дисперсий, следует стремиться к тому, чтобы объемы выборок бы­ли одинаковыми.

В табл. 6 приведен усеченный вариант испытаний рыболовной лески[4]:

- для каждой из технологий 1 и 2 на испытания представлено по пять образцов лески;

- по технологии 3 на испытания представлено три образца лески;

- по технологии 4 на испытания представлено четыре образца лески.

Дисперсионный анализ результатов испытаний, приведенных в табл. 6, выполненный с помощью программы Microsoft Excel, представлен в табл. 7. Итоговые результаты анализа свидетельствуют о том, что, для исходных результатов испытаний, нулевая гипотеза не выполняется, т.к.:

во-первых, F = 3,65 > F кр. = 3,41;

во-вторых, P-знач. = 0,041 < α = 0,05.

Исключив наихудшую технологию 4 и выполнив дисперсионный анализ для оставшихся 3-х технологий, получим итоговые данные (см. табл. 8), которые не дают нам веских оснований для отклонения нулевой гипотезы:

F = 2,60 > F кр. = 4,10;

P-знач. = 0,123 > α = 0,05.

Таким образом, для данных результатов испытаний прочность рыболовной лески, изготовляемой по технологиям 1, 2 и 3, как и ранее – статистически (на уровне значимости α = 0,05) не различима.

Таблица 6

Исходная таблица для дисперсионного анализа р езультатов испытаний рыболовной лески

Результаты испытаний лески	Технология 1	Технология 2	Технология 3	Технология 4
Единичные измерения	34.5	29.5	33.5
29.5			28.5
31.5
	31.5
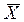
	31,5	30,4	33,5	29,375
S ^2	5,375	3,175	0,25	1,23

Таблица 7

Итоговая таблица дисперсионного анализа результатов испытаний, приведенных в табл. 7

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисп.
Технология 1		157.5	31.5	5.375
Технология 2			30.4	3.175
Технология 3		100.5	33.5	0.25
Технология 4		117.5	29.375	1.23
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-знач.	F кр.
Между группами	32.35		10.78	3.65	0.041	3.41
Внутри групп	38.39		2.95
Итого	70.74

Таблица 8

Итоговая таблица дисперсионного анализа результатов испытаний рыболовной лески, производимой по технологиям 1, 2 и 3

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисп.
Технология 1		157.5	31.5	5.375
Технология 2			30.4	3.175
Технология 3		100.5	33.5	0.25
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-знач.	F кр.
Между группами	18.03		9.01	2.60	0.123	4.10
Внутри групп	34.7		3.47
Итого	52.73

Ниже приведены различные варианты однофакторного дисперсионного анализа, выполненные с помощью программы Microsoft Ехсеl для одного и того же набора экспериментальных данных, приведенных в табл. 9.

Таблица 9

Дата добавления: 2014-11-25