Элементы теории

ЛАБОРАТОРНАЯ РАБОТА

«Инерциальные свойства твердого тела»

Цель работы:

проанализировать зависимость момента инерции тела от его расположения относительно оси вращения;

определить момент инерции параллелепипеда относительно оси, проходящей через его главную диагональ; определить угол между векторами момента импульса и угловой скорости.

1. Метод крутильных колебаний с использованием эталонного тела.

Гармоническим крутильным колебанием тела называется периодическое движение относительно оси, проходящей через центр тяжести этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или косинуса.

Если твердое тело вращается вокруг какой-либо оси, то инертность вращения этого тела зависит не только от его массы, оно зависит и от распределения массы в теле. Поэтому инертность вращения определяется не только массой вращающегося тела (как это наблюдается в поступательном движении), но и физической величиной -- моментом инерции I. (см.краткую теорию к работе М3).

Вращательное движение тела описывается также с помощью следующих кинематических величин: j - угол поворота, w - угловая скорость, e - угловое ускорение (см.краткую теорию к работе М3).

Основным законом динамики вращательного движения является уравнение

(1.1)

где I - момент инерции системы.

Если учесть, что угловое ускорение может быть представлено как , а при повороте тела на угол j от положения равновесия, то со стороны проволоки подвеса к нему будет приложен момент сил, пропорциональный (в пределах упругой деформации проволоки) углу:

(1.2)

где k -- коэффициент упругости проволоки, то уравнение (1) можно переписать в виде.

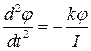
Обозначим

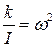(1.3)

получим

Решение этого дифференциального уравнения имеет вид:

,

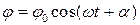т.е. тело будет совершать гармонические колебания около положения равновесия, где j₀ -- угловая амплитуда колебаний, w -- круговая частота, a -- начальная фаза.

Так как период колебаний равен 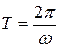, то с учетом формулы (1.3) получаем

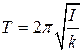(1.4)

Необходимо иметь в виду, что крутильный маятник сам по себе обладает некоторым моментом инерции I₀. Поэтому при наличии тела, момент инерции которого I_T, мы должны считать, что момент инерции системы равен I = I₀ + I_T. Для определения I₀ используется эталонное тело с известным моментом инерции I_эт. Запишем формулу (1.4) для ненагруженного крутильного маятника и крутильного маятника с эталоном, предварительно возведя ее в квадрат:

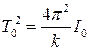
Из этих формул выразим I₀:

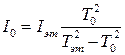(1.5)

Расположив на месте эталонного тела исследуемое, получим аналогичным образом:

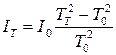(1.6)

где I_T -- момент инерции тела:

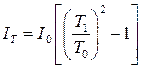(1.7)

Момент инерции эталонного тела относительно оси вращения, проходящей через центр тяжести, находится по стандартным формулам:

а) для однородного цилиндра

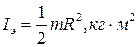(1.8)

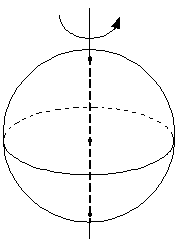б) для однородного шара

(1.9)

где m -- масса тела; R -- радиус тела.

Если твердое тело вращается вокруг какой-либо оси, то инертность вращения этого тела зависит не только от его массы, но также и от распределения массы в теле. Поэтому инертность вращения определяется не только массой вращающегося тела (как это наблюдается в поступательном движении), но и физической величиной - моментом инерции I.

Моментом инерции материальной точки называется произведение массы точки на квадрат расстояния от точки до оси вращения:

(1.10)

Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных частиц с массами Dm_i, на которые можно разбить все данное тело:

(1.11)

где r_i -- кратчайшее расстояние частицы от оси вращения.

Одно и то же тело обладает различными моментами инерции относительно разных осей вращения.

Если ось вращения не проходит через центр тяжести тела, то момент инерции его рассчитывается на основании формулы Штейнера:

(1.12)

где I_o -- момент инерции тела относительно оси вращения, проходящей через центр тяжести и параллельной данной оси; m - масса тела; d - расстояние от оси вращения тела до центра тяжести тела.

Если тело имеет неправильную форму, то вычисление момента инерции крайне затруднительно, и поэтому его определяют опытным путем.

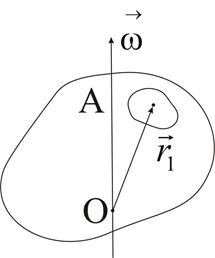Рис. 1

Дата добавления: 2014-11-25