
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Количественные характеристики инерциальных свойств твердого тела
|
|
|
|
Одной из величин, характеризующих вращение твёрдого тела вокруг некоторой точки О (рис. 1) является момент импульса тела 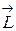 .Чтобы определить момент импульса тела, можно мысленно разбить тело на материальные точки массами
.Чтобы определить момент импульса тела, можно мысленно разбить тело на материальные точки массами 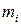 (i - номер точки), найти вектор момента импульса каждой материальной точки, который равен векторному произведению радиус-вектора точки на вектор ее импульса
(i - номер точки), найти вектор момента импульса каждой материальной точки, который равен векторному произведению радиус-вектора точки на вектор ее импульса  , тогда
, тогда  .
.
Пусть тело вращается вокруг оси, проходящей через точку О и 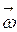 - его мгновенная угловая скорость. Тогда скорость i-той точки тела равна
- его мгновенная угловая скорость. Тогда скорость i-той точки тела равна 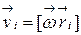 . Поэтому момент импульса тела относительно точки О равен:
. Поэтому момент импульса тела относительно точки О равен:
 (2.1)
(2.1)
Векторное равенство (2.1) можно записать в виде трёх проекций на оси координат:
 (2.2)
(2.2)
Учитывая, что  вместо (2.2) имеем:
вместо (2.2) имеем:
 (2.3)
(2.3)
где
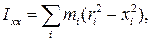

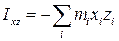 (2.4)
(2.4)
и аналогично выражаются 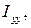

 и т.д. Из (2.4) видно, что
и т.д. Из (2.4) видно, что 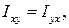
 и т.д. Поэтому из 9 величин
и т.д. Поэтому из 9 величин 
 ... различны лишь 6. Величины
... различны лишь 6. Величины 
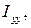
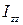 называются осевыми моментами инерции, а
называются осевыми моментами инерции, а 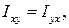

 - центробежными моментами инерции.
- центробежными моментами инерции.
Таким образом, момент импульса тела весьма сложно зависит от распределения масс в теле и его направление не совпадает, вообще говоря, с угловой скоростью вращения тела. Совокупность величин
 (2.5)
(2.5)
называется тензором инерции тела относительно точки О. Величины 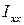 ,
, 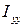 ,
, 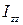 являются диагональными элементами тензора, а остальные - недиагональными. В данном случае величины, расположенные симметрично относительно диагонали, равны. Такой тензор называется симметричным. Если недиагональные элементы тензора равны нулю, а осевые отличны от нуля, то говорят, что оси тела, совпадающие с осями координат, являются главными осями инерции, а величины
являются диагональными элементами тензора, а остальные - недиагональными. В данном случае величины, расположенные симметрично относительно диагонали, равны. Такой тензор называется симметричным. Если недиагональные элементы тензора равны нулю, а осевые отличны от нуля, то говорят, что оси тела, совпадающие с осями координат, являются главными осями инерции, а величины 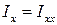 ,
,  ,
, 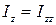 называют главными моментами инерции (часто их можно определить из соображений симметрии). Если главные оси проведены через центр масс, то они называются главными центральными осями. Тело, для которого
называют главными моментами инерции (часто их можно определить из соображений симметрии). Если главные оси проведены через центр масс, то они называются главными центральными осями. Тело, для которого  , а остальные компоненты тензора равны нулю, называется шаровым волчком. При этом
, а остальные компоненты тензора равны нулю, называется шаровым волчком. При этом  , т.е. направление момента импульса совпадает с направлением
, т.е. направление момента импульса совпадает с направлением 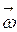 . Если
. Если 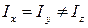 , то тело называется симметричным волчком, а при
, то тело называется симметричным волчком, а при 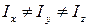 говорят об асимметричном волчке.
говорят об асимметричном волчке.
Вычислим момент инерции 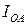 твёрдого тела относительно произвольной оси ОА. Свяжем с точкой О декартовую систему координат и учтем, что
твёрдого тела относительно произвольной оси ОА. Свяжем с точкой О декартовую систему координат и учтем, что 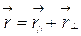 (рис. 2), тогда
(рис. 2), тогда 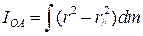 . Пусть
. Пусть 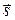 - единичный вектор, направленный вдоль оси ОА, тогда
- единичный вектор, направленный вдоль оси ОА, тогда
 Рис. 2
Рис. 2
|
 ,
, 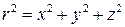 .
.
Подставляя 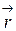 и
и 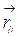 в выражение для
в выражение для 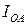 и учитывая, что
и учитывая, что  , получаем:
, получаем:
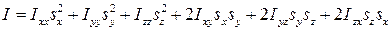 ,
,
где 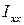 ,
,  ,
,  и т.д. компоненты тензора инерции.
и т.д. компоненты тензора инерции.
Если оси координат являются главными центральными осями, то
 . (2.6)
. (2.6)
Теория метода. Колебательное движение крутильного маятника описывается уравнением, которое в проекции на ось вращения z имеет вид:
 , (2.7)
, (2.7)
где Mz - момент сил упругости относительно оси вращения, сообщающий системе угловое ускорение  ,
, 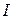 - момент инерции относительно той же оси. Для упругих деформаций (амплитуда колебаний должна быть мала)
- момент инерции относительно той же оси. Для упругих деформаций (амплитуда колебаний должна быть мала)  , где
, где 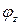 - проекция вектора углового перемещения маятника на ось z (он направлен противоположно вектору момента сил упругости),
- проекция вектора углового перемещения маятника на ось z (он направлен противоположно вектору момента сил упругости),  - модуль кручения. Тогда:
- модуль кручения. Тогда:
 , (2.8)
, (2.8)
или
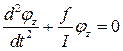 . (2.9)
. (2.9)
Уравнение (2.9) является уравнением гармонических колебаний переменной jz с циклической частотой  . Следовательно
. Следовательно 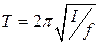 .
.
Обозначим период колебаний рамки 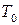 , тогда
, тогда
 ,
,
где  - момент инерции рамки. Для рамки с кубиком
- момент инерции рамки. Для рамки с кубиком
 ,
,
где  - момент инерции кубика с ребром
- момент инерции кубика с ребром  (он равен
(он равен  ). Если в рамке закрепить параллелепипед, то период его колебаний
). Если в рамке закрепить параллелепипед, то период его колебаний 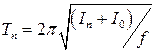 , где
, где 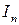 - его момент инерции относительно оси вращения. Для него получаем:
- его момент инерции относительно оси вращения. Для него получаем:
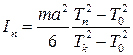
 . (2.10)
. (2.10)
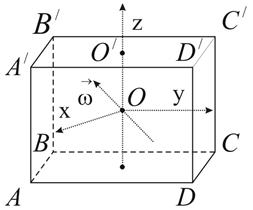 Рис. 3
Рис. 3
|
Рассчитаем момент инерции параллелепипеда относительно оси, проходящей через точки 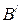 и
и  (см. рис. 3). Пусть
(см. рис. 3). Пусть 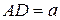 ,
,  ,
,  . Тогда
. Тогда
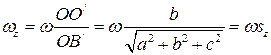 (2.11)
(2.11)
Аналогично
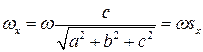 ,
, 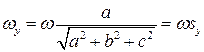
(т.к. 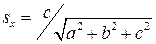 ,
, 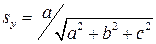 ,
,  ).
).
С учётом (2.6)
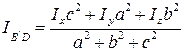 . (2.12)
. (2.12)
Для прямоугольного параллелепипеда
 ,
,  ,
, 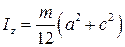 . (2.13)
. (2.13)
Подчеркнём, что в данном случае
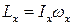 ,
,  ,
,  (2.14)
(2.14)
(оси координат совпадают с главными центральными осями тела). Тогда
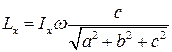 ;
; 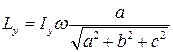 ;
; 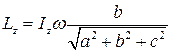 (2.15)
(2.15)
и с учётом
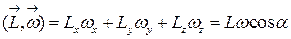
для угла 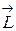 и
и 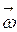 запишем
запишем
 . (2.16)
. (2.16)
С учётом (2.11) получаем
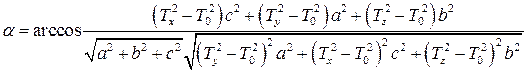 (2.17)
(2.17)
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 637; Нарушение авторских прав?; Мы поможем в написании вашей работы!