Основные формулы по физике Ч. 2

Закон Кулона:

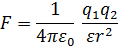
где F - сила взаимодействия точечных зарядов q ₁ и q ₂, r - расстояние между зарядами, ε -диэлектрическая проницаемость, ε₀ - электрическая постоянная.

Напряженность электрического поля и потенциал:

Е = F / q, φ = Е_п/ q,

где Е_п - потенциальная энергия точечного положительного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).

Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:

F =q E, Е_п = qφ.

Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):

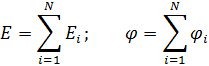
где Е_i , φ _i - напряженность и потенциал в данной точке поля, создаваемые i -м зарядом.

Напряженность и потенциал поля, создаваемого точечным зарядом:

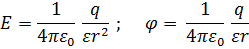
где r - расстояние от заряда q до точки, в которой определяются напряженность и потенциал.

Напряженность и потенциал поля, создаваемого проводящей сферой радиусом R с зарядом q на расстоянии r от центра сферы:

a) E=0, 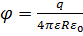; (при r ˂ R),

б) 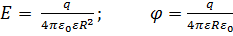; (при r = R),

в) 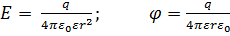; (при r ˃ R)

Линейная плотность заряда:

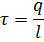
Поверхностная плотность заряда:

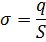
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром:

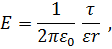
где r - расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:

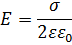
Связь потенциала поля с напряженностью поля:

Е = -grad φ.

Электрический момент диполя:

р = | q | l,

где q - заряд; l - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

Механический (вращательный) момент сил, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е:

М = [ p, E ] или М = рЕ sin α,

где α - угол между направлениями векторов р и Е.

Работа сил поля по перемещению заряда q из точки поля с потенциалом φ₁ в точку с потенциалом φ₂:

А ₁₂ = q (φ₁ - φ₂).

Электроемкость:

С = q / φ или С = q / U,

где φ - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю), U – разность потенциалов пластин конденсатора.

Электроемкость уединенной проводящей сферы радиусом R:

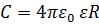
Электроемкость плоского конденсатора:

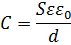
где S - площадь пластины (одной) конденсатора, d – расстояние между пластинами.

Электроемкость батареи конденсаторов:

а) 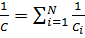(при последовательном соединении);

б) 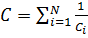(при параллельном соединении).

Энергия заряженного конденсатора:

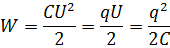
Связь поляризованности P с напряженностью Е среднего макроскопического поля в диэлектрике:

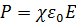
χ - диэлектрическая восприимчивость, ε₀ – электрическая постоянная.

Связь между вектором индукции D и вектором напряженности Е электрического поля в однородных диэлектриках:

D = ε₀ E + P.

Связь диэлектрической проницаемости ε с диэлектрической восприимчивостью χ:

ε = 1 + χ

Связь между поверхностной плотностью связанных зарядов 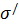и нормальной составляющей вектора поляризованности P_n:

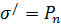
Объемная плотность энергии электростатического поля:

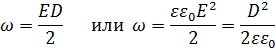
Сила т ока:

I = q / t,

где q -заряд, прошедший через поперечное сечение проводника за время t.

Плотность тока:

j = I / S = en<v>,

где S - площадь поперечного сечения проводника, е – заряд частицы, n- концентрация частиц, v - скорость направленного движения частиц.

Закон Ома для участка цепи, содержащей э.д.с.:

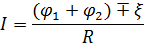
где φ₁-φ₂= U - разность потенциалов (напряжение) на концах участка цепи, ξ - э.д.с. источника тока, R - полное сопротивление участка цепи.

Законы Кирхгофа;

а) 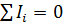(первый закон),

б) 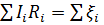(второй закон),

где s w:val="28"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:e></m:nary></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 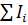- алгебраическая сумма токов, сходящихся в узле; 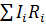- алгебраическая сумма произведений сил токов на сопротивления участков, 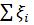- алгебраическая сумма э.д.с.

Сопротивление R и проводимость G проводника:

R = ρ l / S, G = γ S / l,

где ρ - удельное сопротивление, γ - удельная проводимость, l - длина проводника, S - площадь поперечного сечения проводника.

Сопротивление системы проводников:

а) 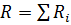(при последовательном соединении),

б) 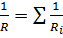(при параллельном соединении),

где R_i - сопротивление i- го проводника.

Работа тока:

A = IU t = I ² R t = U ² t / R.

Мощность тока:

P = IU = I ² R = U ²/ R.

Законы Ома и Джоуля -Ленца в дифференциальной форме:

j = γ E, ω = γ E ²,

где γ - удельная проводимость, Е - напряженность электрического поля, j - плотность тока, ω - плотность мощности, выделяемой в проводнике.

Связь магнитной индукции В с напряженностью H магнитного поля:

B = μμ₀H,

где μ - магнитная проницаемость изотропной среды, μ₀ - магнитная постоянная. В вакууме μ=1, в парамагнетике μ>1, в диамагнетике μ<1, в ферромагнетике μ=μ(H).

Закон Био-Савара-Лапласа:

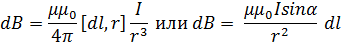
где dB - индукция магнитного поля, создаваемого элементом проводника длиной dl c током I, r -радиус-вектор, направленный от элемента проводника к точке, в которой определяется индукция, α - угол между радиус-вектором и направлением тока в элементе проводника.

Магнитная индукция на оси кругового тока:

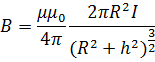
где h - расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током:

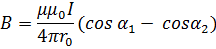
где r ₀ -расстояние от оси проводника до точки, в которой определяется магнитная индукция; α₁ и α₂ - углы между направлением тока и радиус векторами, проведенными из концов проводника в точку наблюдения.

Магнитная индукция поля длинного соленоида:

В = μμ₀ nI,

где n - отношение числа витков соленоида к его длине.

Сила, действующая на проводник с током в магнитном поле (закон Ампера):

dF = I [ dl, B ] или dF = Ibdl sinα,

где dl - длина элемента проводника, α - угол между направлением тока в проводнике и вектором магнитной индукции В.

Магнитный момент плоского контура с током:

р _m = nIS,

где n - единичный вектор нормали (положительной) к плоскости контура, I - сила тока, проходящего по контуру; S – площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:

М = [ p _m, B ] или М = р _m B sin α,

где α - угол между векторами р _m и В.

Потенциальная энергия (механическая) контура с током в магнитном поле:

E _мех = - р _m B или E _мех = - р _m В cos α.

Отношение магнитного момента р _m к механическому L (моменту импульса) заряженной частицы, движущейся покруговой орбите:

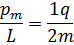
где q - заряд частицы, m - масса частицы.

Сила Лоренца:

F = qE + q [ v, B ],

где q - заряд частицы. v - скорость частицы, Е – вектор напряженности электрического поля, В - вектор магнитной индукции.

Магнитный поток:

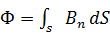(интегрирование ведется по всей поверхности).

В случае однородного поля и плоской поверхности:

Ф = ВS cosα или Ф = В _n S,

где S - площадь контура, a - угол между нормалью к плоскости контура и вектором магнитной индукции.

Работа по перемещению замкнутого контура в магнитном поле:

А = I Δ Ф.

Э.д.с. индукции:

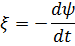
где ψ - потокосцепление (полный поток через N контуров).

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:

q= Δ Ф / R или q = N Δ Ф / R = Δψ/ R,

где R - сопротивление проводника.

Индуктивность контура:

L=ψ / I

Э.д.с. самоиндукции:

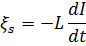
Индуктивность солнеоида:

L = μμ₀ n ² V,

где n - отношение числа витков соленоида к его длине, V – объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

а) 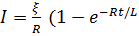(при замыкании цепи),

где ξ - э.д.с. источника тока, t - время, прошедшее после замыкания цепи;

б) I = I ₀ e^{- Rt / L} (при размыкании цепи),

где I ₀ - сила тока в цепи при t =0, t - время, прошедшее с момента размыкания цепи.

Энергия магнитного поля соленоида:

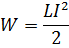
Объемная плотность энергии магнитного поля (энергия

магнитного поля, сосредоточенная в единице объема):

ω = BH /2 или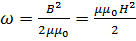

где В - магнитная индукция, Н - напряженность магнитного поля.

Период собственных колебаний в контуре без активного сопротивления (формула Томсона):

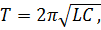
где L - индуктивность контура, С - электроемкость контура.

Добротность колебательного контура в случае малого затухания ((R /2 L)² << ω₀², где 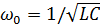- собственная частота контура):

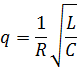
Связь длины λ, периода Т и частоты w электромагнитной волны:

λ = cT, λ = 2π c /ω,

где с - скорость электромагнитной волны в вакууме (с =3.108 м/с).

Скорость света в среде:

v = c/n,

где c - cкорость света в вакууме; n - показатель преломления среды.

Оптическая длина пути световой волны:

L = nl,

где l -геометрическая длина пути световой волны в среде с показателем преломления n.

Оптическая разность хода двух световых волн:

Δ= L ₁ - L ₂.

Связь разности фаз с оптической разностью хода световых волн:

Δφ = 2pΔ/λ,

где λ - длина световой волны.

Условие интерференционных максимумов:

Δ = ± k λ, (k = 0,1,2,...),

где k - порядок интерференции.

Условие интерференционных минимумов:

Δ = ±(2 k+ 1)λ / 2, (k = 0,1,2,...).

Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки:

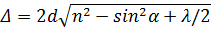
или

Δ = 2 dnCos β + λ / 2,

где d - толщина пленки, n - показатель преломления пленки, α - угол падения, β - угол преломления света в пленке.

Радиусы светлых колец Ньютона в отраженном свете и темных колец в проходящем свете:

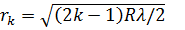(k = 1, 2, 3,...),

где k - номер кольца, R - радиус кривизны линзы.

Радиусы темных колец Ньютона в отраженном свете и светлых колец в проходящем свете:

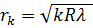(k = 1, 2, 3,...).

Радиусы зон Френеля для сферической волны:

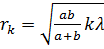(k = 1, 2, 3,...),

где k - номер зоны, а - расстояние от источника до фронта волны, b -расстояние от фронта волны до центра экрана.

Радиусы зон Френеля для плоской волны:

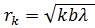(k = 1, 2, 3,...).

Условие дифракционного минимума при дифракции на одной щели:

bSin φ = ± k λ, (k = 1,2,3,...),

где k - номер минимума, φ - угол дифракции, b - ширина щели.

Условие дифракционного максимума при дифракции на одной щели:

bSin φ = ±(2 k+ 1)λ/2, (k = 0,1,2,3,...).

Условие главных дифракционных максимумов при дифракции на решетке:

dSin φ = ± k λ, (k = 0,1,2,3,...),

где d - период дифракционной решетки.

Условие дополнительных минимумов при дифракции на решетке:

dSin φ = ± k’/N, (k’ = 1, 2, 3,..., кроме 0, N, 2 N, 3 N,...),

где N - число щелей решетки.

Разрешающая способность дифракционной решетки:

R = λ / Δλ = kN,

где Δλ - наименьшая разность длин волн двух соседних спектральных линий, при которой эти линии могут быть видны раздельно в спектре, λ - длина волны, вблизи которой производятся измерения.

Угловая дисперсия дифракционной решетки:

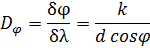
где δφ - угловое расстояние между двумя спектральными линиями с разностью длин волн δλ.

Линейная дисперсия дифракционной решетки:

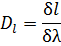
где δ l - линейное расстояние между двумя спектральными линиями с разностью длин волн δλ.

Формула Вульфа-Брэгга для дифракции рентгеновских лучей:

2 dSin θ = k λ,

где θ - угол скольжения, d - расстояние между атомными плоскостями.

Степень поляризации света:

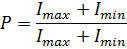
где I_max и I_min - максимальная и минимальная интенсивности света, пропускаемые поляризатором.

Закон Бюстера:

tg α _Б = n ₁₂,

где α _Б - угол падения, при котором отразившийся от диэлектрика свет полностью поляризован, n ₁₂ - относительный показатель преломления второй среды относительно первой.

Закон Малюса:

I = I _o Cos² φ,

где I₀ - интенсивность света, падающего на поляризатор, I - интенсивность этого света после поляризатора, φ - угол междунаправлением колебаний светового вектора и плоскостьюпропускания поляризатора.

Угол поворота плоскости поляризации при прохождении света через оптически активное вещество:

φ = αd (в твердых телах),

где α - постоянная вращения; d - длина пути, пройденного светом в оптически активном веществе;

j = [α]ρ d (в растворах),

где [α] - удельное вращение; ρ - массовая концентрация оптически активного вещества в растворе.

Угол поворота плоскости поляризации в эффекте Фарадея:

φ = VdH,

где V - постоянная Верде, Н - напряженность магнитного поля соленоида, d - длина соленоида.

Взаимосвязь массы и энергии релятивистской частицы:

E = mc² или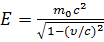

где Е_о=m_oc² - энергия покоя частицы, m₀ - масса покоя частицы, m - релятивистская масса, v - скорость частицы.

Полная энергия свободной частицы:

Е = Е₀ + Т,

где T - кинетическая энергия частицы.

Кинетическая энергия релятивистской частицы:

T = (m - m₀)c² или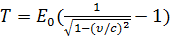

Импульс релятивистской частицы:

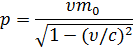
Связь полной энергии и импульса релятивистской частицы:

Закон Кирхгофа:

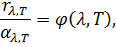
где r _{λ T} - испускательная способность тела, α_{λ T} – поглощательная способность, φ(λ ,T) - универсальная функция Кирхгофа, Т - температура тела.

Закон Стфеана-Больцмана:

R_э= σТ⁴,

где R_э- энергетическая светимость абсолютно черного тела, σ - постоянная Стефана-Больцмана.

Энергетическая светимость серого тела:

R_э= ασ Т⁴,

где α - коэффициент поглощения серого тела (степень черноты).

Закон смещения Вина:

λ _mT = b,

где λ _m - длина волны, на которую приходится максимум испускательной способности абсолютно черного тела, b - постоянная Вина.

Максимальное значение испускательной способности абсолютно черного тела для данной температуры:

r_max = cT⁵,

где константа с= 1,3·10^{- 5} Вт/м³К⁵.

Энергия фотона:

ε= h ν или ε = hc/ λ,

где ν - частота фотона.

Масса фотона:

m = ε /c².

Импульс фотона:

p = mc = h/λ.

Формула Эйнштейна для фотоэффекта:

h ν = A + T_max,

где А - работа выхода электрона, T_max – максимальная кинетическая энергия фотоэлектрона.

Красная граница фотоэффекта:

λ₀ = hc/A.

Коротковолновая граница сплошного рентгеновского спектра:

λ _min = hc/eU,

где e - заряд электрона, U - ускоряющая разность потенциалов в рентгеновской трубке.

Давление света при нормальном падении на поверхность:

p = E_э (1+ρ)/ c = w (1+ρ),

где Е_э - энергетическая освещенность, w - объемная плотность энергии излучения, ρ - коэффициент отражения поверхности; или

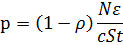
где N - число фотонов, падающих на поверхность, S – площадь поверхности, t - время облучения, ε - энергия фотона.

Формула Комптона:

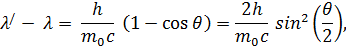
где λ - длина волны падающего фотона, λ ^/ - длина волны рассеянного фотона, θ - угол рассеяния, m₀ - масса покоя электрона.

Обобщенная сериальная формула Бальмера:

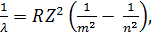(n = m +1, m +2,...),

где R - постоянная Ридберга, m и n - главные квантовые числа, Z - порядковый номер химического элемента.

Первый постулат Бора:

m ₀ v _n r _n = nh/2 π, (n = 1,2,3,...),

где m ₀ - масса электрона, v_n - скорость электрона на n- ой орбите, r_n - радиус n- ой стационарной орбиты, n - главное квантовое число.

Энергия, излучаемая или поглощаемая атомом водорода:

ε = h ν = E_m - E_n,

где E_m и E_n - энергии стационарных состояний атома со значениями главного квантового числа m и n.

Радиус n- ой стационарной орбиты водородоподобных атомов:

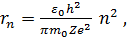(n = 1,2,3,...).

где ε ₀ - электрическая постоянная.

Радиус стационарной орбиты в атоме водорода:

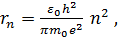(n = 1,2,3,...).

Энергия электрона в водородоподобном атоме:

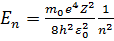, (n = 1,2,3,...).

Длина волны де Бройля:

λ = h/p,

где p - импульс частицы.

Соотношение неопределенностей:

∆ x ∆ p ³ ≥ h/ 2π,

где ∆ x- неопределенность координаты, ∆ p – неопределенность проекции импульса на ось x.

Энергия связи нуклонов в ядре:

E_св = с² { Zm_H+ (A - Z) m_n - m_a },

в том числе удельная энергия связи

E_уд = E_св/A,

где mH - масса атома водорода, mn - масса нейтрона, ma – масса атома, A - массовое число, Z - зарядовое число.

Закон радиоактивного распада:

N = N₀e^{- λ t} ,

где N - число ядер, не распавшихся к моменту времени t; N₀ - число ядер в начальный момент времени, λ - постоянная распада.

Период полураспада:

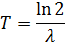
Активность радиоактивного изотопа:

A = A₀e- ^{λ t} или А = λ N,

где А₀ - активность в начальный момент времени.

Энергетический эффект ядерной реакции:

Q = c² (Σ m_i - Σm_k),

где S m_i - сумма масс ядер или частиц, вступающих в реакцию, S m_k - сумма масс продуктов реакции.

Дата добавления: 2014-11-25