
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Какой из приведенных символов не связан функциональной зависимостью количественного, качественного и объемного показателей?
|
|
|
|
Тесты
Агрегатные индексы. Агрегат – сложный экономический показатель, получаемый путем произведения непосредственно не суммируемых взаимосвязанных величин с последующим суммированием результатов умножения. Такие расчеты выражают аддитивно-муль-типликативную зависимость. Агрегатные индексы являются общими.
Общие индексы объёмных показателей строятся аналогично индивидуальным индексам. Последовательность записи формулы об-щего индекса некоторого объёмного показателя (M) можно представить следующим образом:  .
.
Тогда, например, формулы общих индексов отдельных объёмных показателей записываются в следующем виде:
Ø индекс стоимости:  или
или  , т.к.
, т.к.  ;
;
Ø индекс общих затрат:  или
или  , т.к.
, т.к. 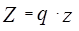 ;
;
Ø индекс валового сбора: 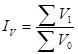 или
или  , т.к. V = h · u.
, т.к. V = h · u.
Построение общих индексов количественных показателей, суммируемых в натуральном выражении, осуществляется аналогично агрегатным индексам объемных показателей, а именно: суммируются отдельные значения показателя в каждом из сравниваемых периодов и полученные суммы соотносятся между собой. Например:
индекс затрат труда:  ; индекс посевных площадей:
; индекс посевных площадей: 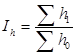 .
.
При построении общих индексов количественных показателей, непосредственно несуммируемых в натуральном выражении, необходимо предварительно привести их к сопоставимому виду. Это достигается чаще всего путем выражения показателя в денежном измерении (через цену - “ р ” или себестоимость - “ z ”). Качественные показатели-соизмерители (веса) не должны влиять на динамику анализируемого количественного показателя и их следует взять неизменными, т.е. на уровне одного периода (как правило базисного) и в числителе, и в знаменателе индекса.
Формула общего индекса физического объёма и последовательность её построения следующая:

При построении агрегатных индексов качественных показателей также возникает проблема соизмерения (взвешивания), т.к. суммирование отдельных значений качественных показателей (показателей уровня) лишено смысла. Показателями-соизмерителями (весами) при этом выступают только те количественные, на единицу которых рассчитаны индексируемые качественные показатели. Количественные показатели-веса принято фиксировать на уровне отчетного периода. Последовательность записи формулы, например, общего индекса цен будет следующей: 
Агрегатные индексы других качественных показателей имеют вид: выработки (производительности труда) -  ; урожайности -
; урожайности - 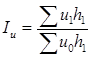 ; трудоемкости -
; трудоемкости - 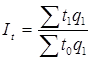 и т. д.
и т. д.
Разность между числителем и знаменателем соответствующих агрегатных индексов позволяет установить абсолютную величину изменения объемного показателя в целом, а также под влиянием отдельно количественного и качественного показателей-факторов. Знак полученной разности укажет на направление изменений: рост (+) или снижение (–).
Например, общее абсолютное изменение стоимости продукции (объемного показателя) находится как разность числителя и знаменателя агрегатного индекса стоимости:

 -
-  (напомним, что
(напомним, что 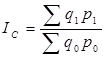 ).
).
Абсолютный прирост стоимости товаров за счет изменения их количества (физического объема) будет равен:

 -
-  (напомним, что
(напомним, что 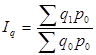 ).
).
Абсолютный прирост стоимости товаров за счет изменения их цен:

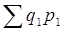 -
-  (напомним, что
(напомним, что  ).
).
Таким образом, агрегатные индексы количественных и качественных показателей выступают аналитическими индексами, т.е. измерителями роли показателей-факторов в общей динамике объёмного показателя. Это требует их взаимосвязи.
Индексы показателей связаны точно также, как связаны сами показатели, т.е. если C = q · p, то и  ; если Z = q · z, то и
; если Z = q · z, то и 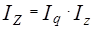 ; если T = q · t, то и
; если T = q · t, то и 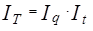 и т.д.
и т.д.
Покажем эту взаимосвязь на примере индексов стоимости, физического объема и цен:  =
= 

 =
=  .
.
Средние из индивидуальных индексов. Средние из индивидуальных индексов образуются из агрегатной формы индекса, когда нет данных об абсолютных значениях индексируемой величины за базис-ный и отчетный периоды, но известно относительное её изменение в динамике (индивидуальный индекс). При этом из формулы индиви-дуального индекса выводят недостающую для агрегатного индекса величину и полученное выражение подставляют в исходную формулу.
Так, агрегатный индекс физического объема ( ) преобразовы-вается в средний арифметический индекс, когда из формулы индивидуального индекса физического объема (
) преобразовы-вается в средний арифметический индекс, когда из формулы индивидуального индекса физического объема (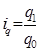 ) выводят величину числителя:
) выводят величину числителя:  и полученное выражение подставляют в числитель агрегатного индекса
и полученное выражение подставляют в числитель агрегатного индекса  ; агрегатный индекс цен (
; агрегатный индекс цен ( ) преобразовыва-ется в средний гармонический индекс, когда из формулы индивидуального индекса цены (
) преобразовыва-ется в средний гармонический индекс, когда из формулы индивидуального индекса цены ( ) находится знаменатель:
) находится знаменатель: 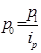 и полученное выражение подставляется в знаменатель агрегатного индекса цен -
и полученное выражение подставляется в знаменатель агрегатного индекса цен - 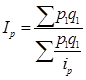 .
.
Индексы средних величин. Из трех видов показателей, выделяемых в индексном анализе, осредняют индивидуальные значения только качественных. Расчет их средних уровней ведут по формуле средней арифметической взвешенной (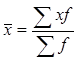 ). Например:
). Например:
- средняя цена некоторого товара “А”, продаваемого несколькими торговыми предприятиями, будет равна: 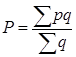
где p - цена товара “А” на каждом торговом предприятии; q - количество товара “А”, проданного каждым торговым предприятием;
- средняя себестоимость некоторого изделия “С”, производимого несколькими предприятиями:
 ,
,
где z - уровень себестоимости изделия “С” на каждом предприятии, q - количество изделий данного вида, произведенного каждым предприятием.
Относительная оценка изменения во времени среднего уровня качественного показателя ведется с помощью индекса переменного состава, который, например, для средней цены имеет вид:
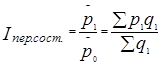 :
:  =
= 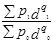 .
.
Разность числителя и знаменателя этого индекса устанавливает абсолютное изменение анализируемого показателя
 .
.
Чтобы установить, как изменилась величина среднего показателя за счет изменения только индивидуальных значений осредняемого признака (в нашем примере - индивидуальных цен), рассчитывают индекс постоянного (фиксированного) состава. Применительно к показателю средней цены он имеет вид:

 :
: 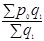 =
=  .
.
Если найти разность числителя и знаменателя индекса фиксированного состава, будет получено абсолютное изменение средней цены за счет изменений в отчетном периоде по сравнению с базисным индивидуальных цен товара, продаваемого разными объектами: 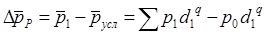
Влияние изменений в структуре совокупности на динамику среднего показателя устанавливают с помощью индекса структурных сдвигов. Покажем его вид на примере средней цены:

 :
:  =
=  .
.
Чтобы установить на сколько изменилась средняя цена товара в результате изменения в структуре ее реализации нужно вычислить разность числителя и знаменателя индекса структурных сдвигов.

 .
.
Прикладные индексные модели. Рассмотренные принципы построения индексов не являются единственно возможными в экономико-статистическом анализе. Так, агрегатный индекс цен с весами, зафиксированными на уровне отчетного периода ( ), называется индексом Пааше и используется, как было отмечено, в оценке динамики розничных цен. Несколько иной результат будет получен, если применить веса базисного периода:
), называется индексом Пааше и используется, как было отмечено, в оценке динамики розничных цен. Несколько иной результат будет получен, если применить веса базисного периода: 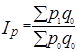 . Этот индекс служит основой для расчета индекса потребительских цен и называется формулой Ласпейреса. Он позволяет установить изменение потребительских расходов в текущем периоде по сравнению с базисным, если при изменении цен уровень и структура потребления останутся прежними. Поэтому значение данного индекса в оценке динамики цен возрастает в условиях высоких темпов инфляции, когда как раз не происходит существенных изменений ни в объеме, ни в структуре потребления.
. Этот индекс служит основой для расчета индекса потребительских цен и называется формулой Ласпейреса. Он позволяет установить изменение потребительских расходов в текущем периоде по сравнению с базисным, если при изменении цен уровень и структура потребления останутся прежними. Поэтому значение данного индекса в оценке динамики цен возрастает в условиях высоких темпов инфляции, когда как раз не происходит существенных изменений ни в объеме, ни в структуре потребления.
Средняя геометрическая из индексов Пааше и Ласпейреса получила название “индекс Фишера”: 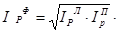 Данная формула применяется в случаях трудностей с выбором весов или значительного изменения структуры весов.
Данная формула применяется в случаях трудностей с выбором весов или значительного изменения структуры весов.
В статистической теории известен индекс цен, получивший название формулы Эджворта-Маршалла:  .
.
Многие сложные экономические явления описываются смешанной (аддитивно-мультипликативной) функциональной зависимостью. Так, например, среднюю производительность труда одного работника (W) можно представить произведением четырех показателей-факто-ров: средней часовой производительности труда (wчас), средней продолжительности рабочего дня (tчас), средней продолжительности рабочего периода (tдн), долей рабочих в общей численности работников предприятия (dр). Общий вид модели будет таким: W = wчас· tчас· tдн · dр
Для установления влияния каждого показателя-фактора (сомножителя) на результативный показатель-функцию (W) в индексном анализе используются два подхода:1) схема обособленного учета влияния факторов; 2) последовательно-цепная схема разложения.
Каждый из них имеет свои достоинства и недостатки. Покажем их, обозначив показатели-факторы буквами: “ а ”, “ в ”, “ с ”, “ d ”, а результативный показатель-функцию буквой “ У ”.
При определении влияния каждого фактора методом их обособленного учета любой частный индекс (субиндекс) строят в предположении, что изменяется от базисного периода к отчетному уровень только данного фактора, величины же всех остальных показателей остаются неизменными, зафиксированными на уровне базисного периода. При данной схеме не имеет значения очередность рассмотрения факторов (это достоинство метода), т.к. при любой очередности получают одинаковые результаты. Но произведение частных индексов не дает полной взаимосвязи с общим индексов (в этом состоит недостаток метода):
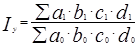 ≠
≠ 
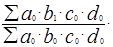

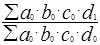 .
.
При определении влияния факторов последовательно-цепным методом (с помощью взаимосвязанных частных индексов) предполагают, что факторы оказывают свое влияние на изменение экономического явления в определенной последовательности, при этом каж-
дый следующий фактор действует при условии уже изменившихся ранее учтенных факторов. Достоинство и недостаток первого метода меняются местами, а именно: произведение частных индексов дает общий индекс, но возникает вопрос о том, в какой последовательности должны быть расположены и рассмотрены факторы. От этого зависит размер изменения явления, приписываемый каждому из них. Другими словами, в первую очередь необходимо решить, какой из двух очередностей отдать предпочтение: a в с d



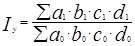 =
= 
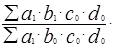
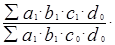



 или d c b a:
или d c b a:
 =
= 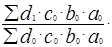


 .
.


 В решении этой проблемы исходят из общепринятого правила взвешивания при построении индексов: веса – качественные показатели берутся базисными, а веса – количественные показатели следует фиксировать на уровне отчетного периода. В соответствии с этим требованием, в первую очередь, необходимо учитывать влияние количественных показателей-факторов, а очередность расположения всех факторов должна быть такой, чтобы еще не рассмотренные факторы в произведении давали качественный показатель. Это положение в нашем случае требует очередности: d c b a:
В решении этой проблемы исходят из общепринятого правила взвешивания при построении индексов: веса – качественные показатели берутся базисными, а веса – количественные показатели следует фиксировать на уровне отчетного периода. В соответствии с этим требованием, в первую очередь, необходимо учитывать влияние количественных показателей-факторов, а очередность расположения всех факторов должна быть такой, чтобы еще не рассмотренные факторы в произведении давали качественный показатель. Это положение в нашем случае требует очередности: d c b a:
Примирить оба подхода возможно с помощью приема, который получил название цепных показателей. Относительное влияние каждого фактора на общую динамику результативного показателя устанавливается при этом через соотношение соответствующих индексов: в числителе дроби берется разность индексов числителя и знаменателя расчетной формулы показателя-фактора, а в знаменателе – индекс знаменателя расчетной формулы показателя-функции. Для нахождения абсолютного изменения показателя-функции за счет каждого фактора достаточно каждый цепной относительный показатель умножить на уровень результативного показателя-функции в базисном периоде (см. решение типовой задачи 6).
1) t; 2) q; 3) p; 4) T.
2. Каким показателем является объем продукции (q) в следующем выражении: q = T· w?
1) количественным; 2) качественным; 3) объемным.
3. Каким показателем является объем продукции (q) в выражении: T = q· w?
1) количественным; 2) качественным; 3) объемным.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1962; Нарушение авторских прав?; Мы поможем в написании вашей работы!